Содержание
- 2. Цели урока: Познакомиться с единичной окружностью и радианной мерой угла Научиться вычислять градусную меру угла, выраженного
- 3. Единичной окружностью называется окружность с центром в начале координат и радиусом, равным единице. R R R
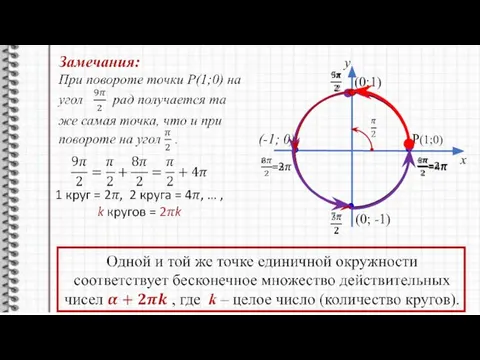
- 6. + - M (α > 0) (α N У х 0 Положительные и отрицательные углы в
- 7. y x P(1;0) M(0;1) N(0; -1) K(-1; 0)
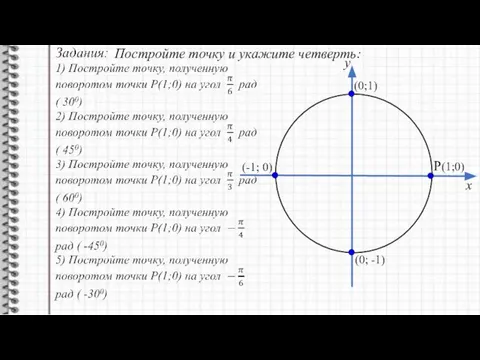
- 8. y x P(1;0) (0;1) (0; -1) (-1; 0) Постройте точку и укажите четверть:
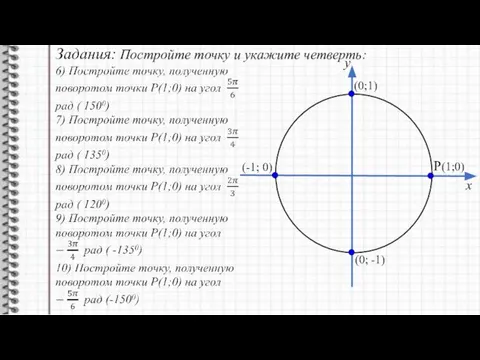
- 9. y x P(1;0) (0;1) (0; -1) (-1; 0) Постройте точку и укажите четверть:
- 10. y x P(1;0) (0;1) (0; -1) (-1; 0)
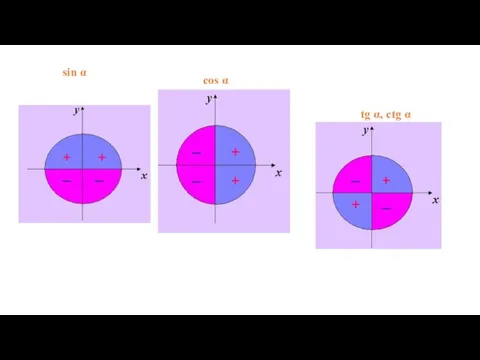
- 11. Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса угла.
- 12. Синусом угла α называется ордината точки, полученная поворотом точки (1;0) вокруг начала координат на угол α.
- 14. Домашнее задание: 1. Используя данные формулы, заполните таблицу:
- 16. Скачать презентацию









 Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Комбинаторные задачи
Комбинаторные задачи Подобные треугольники
Подобные треугольники Единицы измерения времени. Тренажёр
Единицы измерения времени. Тренажёр Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Аксиомы стереометрии о взаимном расположении точек, прямых и плоскостей в пространстве
Аксиомы стереометрии о взаимном расположении точек, прямых и плоскостей в пространстве 6f20c70ecac24a5caad72fa88b388b76
6f20c70ecac24a5caad72fa88b388b76 Презентация на тему Функция арифметического квадратного корня, её свойства
Презентация на тему Функция арифметического квадратного корня, её свойства  Теорема Пифагора
Теорема Пифагора Построение сечений параллелепипеда (задачи)
Построение сечений параллелепипеда (задачи) Возможности применения препаратов на основе гиалуроновой кислоты в стоматологической практике
Возможности применения препаратов на основе гиалуроновой кислоты в стоматологической практике Презентация на тему Неравенства
Презентация на тему Неравенства  Координаты вектора
Координаты вектора Алгоритмически неразрешимые задачи и вычислимые функции
Алгоритмически неразрешимые задачи и вычислимые функции Урок-игра. Аукцион математических знаний
Урок-игра. Аукцион математических знаний Понятие предиката и кванторы. Логические операции над предикатами
Понятие предиката и кванторы. Логические операции над предикатами Формулы сокращенного умножения. Космический час на планете знаний
Формулы сокращенного умножения. Космический час на планете знаний Л 7 Предел числовой последовательности
Л 7 Предел числовой последовательности Учим состав чисел с Колобком
Учим состав чисел с Колобком Презентация на тему Высказывания со словами: есть, существует, некоторые
Презентация на тему Высказывания со словами: есть, существует, некоторые  Деление на 5
Деление на 5 Верхняя, нижняя сумма Дарбу
Верхняя, нижняя сумма Дарбу Множества. Операции над множествами
Множества. Операции над множествами Криволинейные интегралы
Криволинейные интегралы Задачи на концентрацию
Задачи на концентрацию Титло
Титло Многогранники. Основные понятия
Многогранники. Основные понятия Функции и предупреждающие знаки дорожного движения. 11 класс
Функции и предупреждающие знаки дорожного движения. 11 класс