Cхема (метод) Горнера. Способ деления многочлена

Алгоритм вычисления
Схема Горнера - это алгоритм вычисления значения многочлена при определенном значении переменной. Использование схемы Горнера значительно упрощает вычисления, а также помогает эффективно подбирать корни.

Алгоритм вычисления
Схема Горнера - это алгоритм вычисления значения многочлена при определенном значении переменной. Использование схемы Горнера значительно упрощает вычисления, а также помогает эффективно подбирать корни.

Горнер Вильямc Джордж
Горнер Вильямc Джордж (1786-22.9.1837)-английский математик. Родился в Бристоле. Учился и работал там же, затем в школах Бата. Основные труды по алгебре. В 1819г. опубликовал способ приближенного вычисления вещественных корней многочлена, который называется теперь способом Руффини-Горнера (этот способ был известен китайцам еще в XIII в.) Именем Горнера названа схема деления многочлена на двучлен х-а.

Описание алгоритма
Задан многочлен
где n - наибольшая степень, a - коэффициент переменной x.
Делим на линейный двучлен вида
Далее работать придется с таблицей....

Первая строка таблицы заполняется коэффециентами заданного многочлена
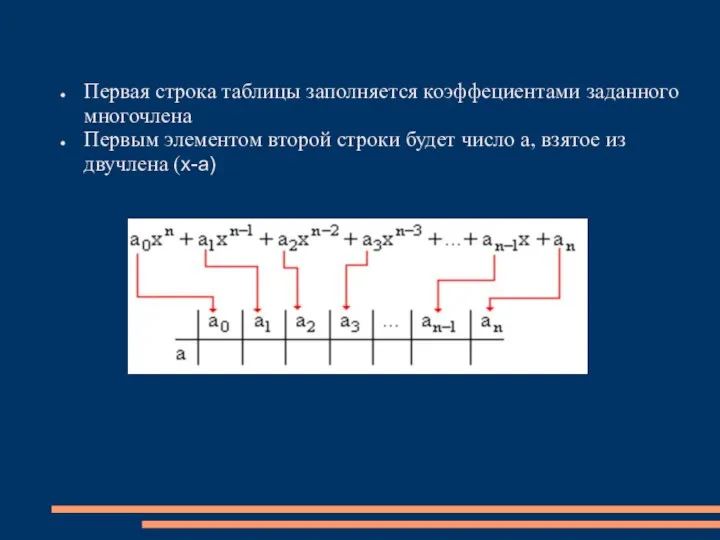
Первым элементом второй строки будет число a, взятое из двучлена (x-a)

Вторая строка заполняется по следующему принципу:
Далее записывается ответ в форме: b0 xn-1+b1xn-2+b2xn-3+b3xn-4...+ остаток

Компактность записи
Основным преимуществом этого метода является компактность записи и возможность быстрого деления многочлена на двучлен. По сути, схема Горнера является другой формой записи метода группировки, хотя, в отличие от последнего, является совершенно ненаглядной. Ответ (разложение на множители) тут получается сам собой, и мы не видим самого процесса его получения. Мы не будем заниматься строгим обоснованием схемы Горнера, а лишь покажем, как она работает.