- Главная
- Математика
- Алгоритм построения графиков, содержащих модуль

Содержание
Слайд 2Способ построения графиков, содержащих модуль ( по определению)
1 каждое подмодульное выражение приравниваем
Способ построения графиков, содержащих модуль ( по определению)
1 каждое подмодульное выражение приравниваем
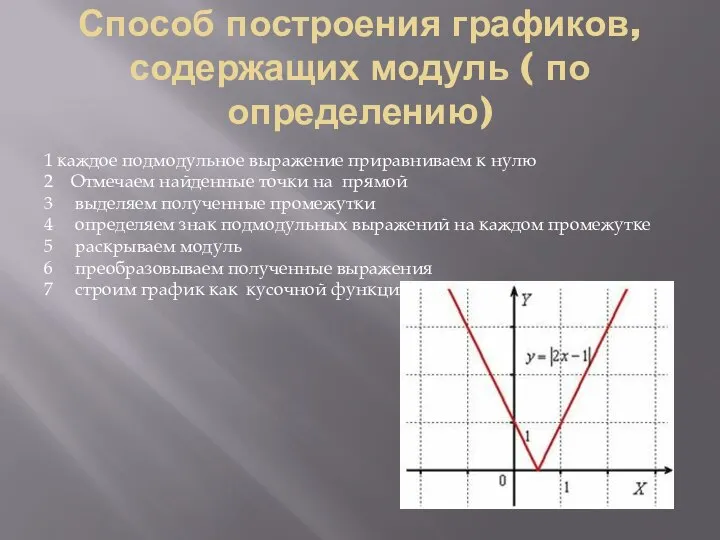
к нулю
Отмечаем найденные точки на прямой
выделяем полученные промежутки
определяем знак подмодульных выражений на каждом промежутке
раскрываем модуль
преобразовываем полученные выражения
строим график как кусочной функции
Отмечаем найденные точки на прямой
выделяем полученные промежутки
определяем знак подмодульных выражений на каждом промежутке
раскрываем модуль
преобразовываем полученные выражения
строим график как кусочной функции
Слайд 3пример
У= | x+3|+ |2x+1|- x
1 x+3= 0 x=-3
2x+1= 0 x= -0,5
2
пример
У= | x+3|+ |2x+1|- x
1 x+3= 0 x=-3
2x+1= 0 x= -0,5
2

числа -3 и – 0, 5 разбили числовую прямую на три промежутка
Определяем знак и раскрываем модуль х < -3 y = - (x + 3) – ( 2x -1)= - 4x -4
- 3 < x< - 0,5 у= х+3 – ( 2х+1) – х = - 2х+ 2
х > - 0, 5 у= х+3+ 2х +1 – х = 2х+ 4
строим график на каждом промежутке.
У= - 4х- 4 , х < - 3
y =- 2x +2, - 3< x <- 0,5
y = 2x+4 x> -0,5
Определяем знак и раскрываем модуль х < -3 y = - (x + 3) – ( 2x -1)= - 4x -4
- 3 < x< - 0,5 у= х+3 – ( 2х+1) – х = - 2х+ 2
х > - 0, 5 у= х+3+ 2х +1 – х = 2х+ 4
строим график на каждом промежутке.
У= - 4х- 4 , х < - 3
y =- 2x +2, - 3< x <- 0,5
y = 2x+4 x> -0,5
 Решение уравнения в 1 классе
Решение уравнения в 1 классе Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Тренажер Состав числа
Тренажер Состав числа Своя игра. Треугольники
Своя игра. Треугольники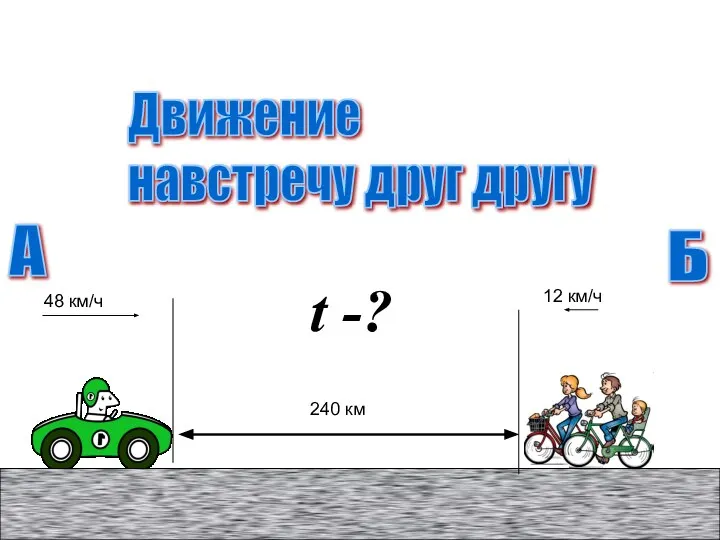 Задачи на движение
Задачи на движение Способы решения уравнений высших степеней
Способы решения уравнений высших степеней Метрологическое обеспечение на базе профессионального стандарта Специалист по метрологии
Метрологическое обеспечение на базе профессионального стандарта Специалист по метрологии Делимость целых чисел
Делимость целых чисел Медиана, биссектриса, высота
Медиана, биссектриса, высота Решение задач по теме: Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике
Решение задач по теме: Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике Урок математики
Урок математики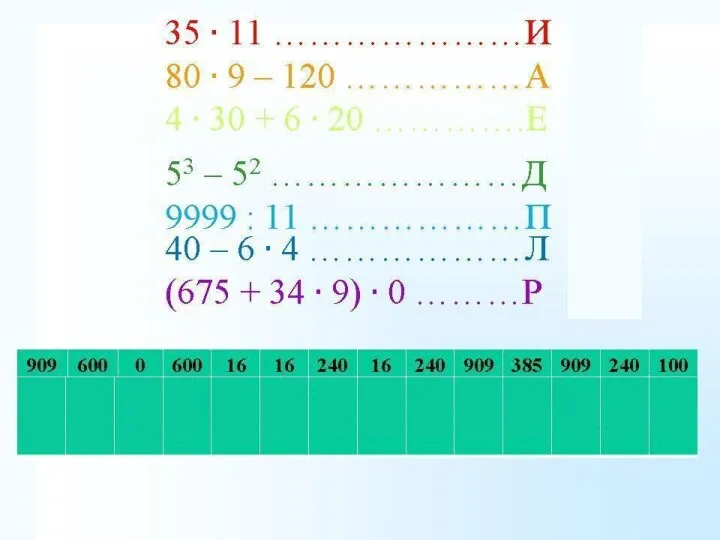 Измерение параллеппипеда
Измерение параллеппипеда Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Раскрытие скобок
Раскрытие скобок Набор инсулина в шприц
Набор инсулина в шприц Сложение и умножение
Сложение и умножение Способы задания зависимостей между величинами: аналитический, табличный, графический
Способы задания зависимостей между величинами: аналитический, табличный, графический Умножение десятичных дробей
Умножение десятичных дробей Начерти два отрезка
Начерти два отрезка Радианная мера угла. Синус, косинус, тангенс числа
Радианная мера угла. Синус, косинус, тангенс числа Расстояние от точки до фигуры
Расстояние от точки до фигуры Четыре замечательные точки треугольника. 8 класс
Четыре замечательные точки треугольника. 8 класс Сложение и вычитание однозначных чисел
Сложение и вычитание однозначных чисел Измерение углов
Измерение углов Деление на 2, 3, 4, 5 (повторение)
Деление на 2, 3, 4, 5 (повторение) Тригонометрические неравенства Слайды для урока по теме:
Тригонометрические неравенства Слайды для урока по теме: Тест по теме Цилиндр
Тест по теме Цилиндр Решение задач. 2 класс
Решение задач. 2 класс