Теория моделирования и анализа факторных систем в экономике

Виды взаимосвязи между явлениями

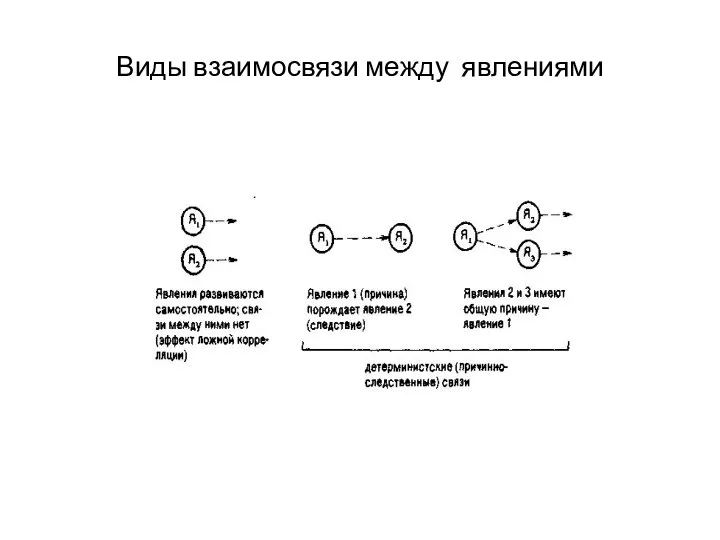
Су­ществуют два типа связей, которые подвергаются исследованию в процессе факторного анализа: функциональные и стохасти­ческие.
Связь называется функциональной, или жестко детерминиро­ванной, если каждому значению факторного признака соответ­ствует вполне определенное неслучайное значение результатив­ного признака.

Связь называется стохастической (вероятностной), если каж­дому значению факторного признака соответствует множество значений результативного признака, т. е. определенное статисти­ческое распределение. Примером такой зависимости могут слу­жить регрессионные уравнения, применяемые, например, при рас­чете бета-коэффициентов для анализа портфельных инвестиций.

Интерпретация рассмотренных связей (функциональной и стохастической) с позиции поведения системы:
Система называется жестко детерминированной, если при заданных начальных условиях она переходит в единственное, определенное состояние.
Система называется вероятностной, если при одних и тех же начальных условиях она может переходить в различные состояния, имеющие разные вероятности.

Рассмотренные связи могут быть прямыми и обратными. В первом случае рост (убывание) факторного признака влечет за собой рост (убывание) результативного признака. Во втором случае рост (убывание) факторного признака влечет за собой убывание (рост) результативного признака.
При изучении связей в финансовом анализе решается несколь­ко задач:
установление факта наличия или отсутствия связи между анализируемыми показателями;
измерение тесноты связи;
установление неслучайного характера выявленных связей;
количественная оценка влияния изменения факторов на изме­нение результативного показателя;
выделение наиболее значимых факторов, определяющих пове­дение результативного показателя.

В зависимости от вида анализа эти задачи решаются с помо­щью различных приемов:
а) жестко детерминированные связи - балансовый метод, прием цепных подстановок, интегральный метод и др.;
б) стохастические связи — корреляционный анализ, ковариационный анализ, метод главных компонент и др.

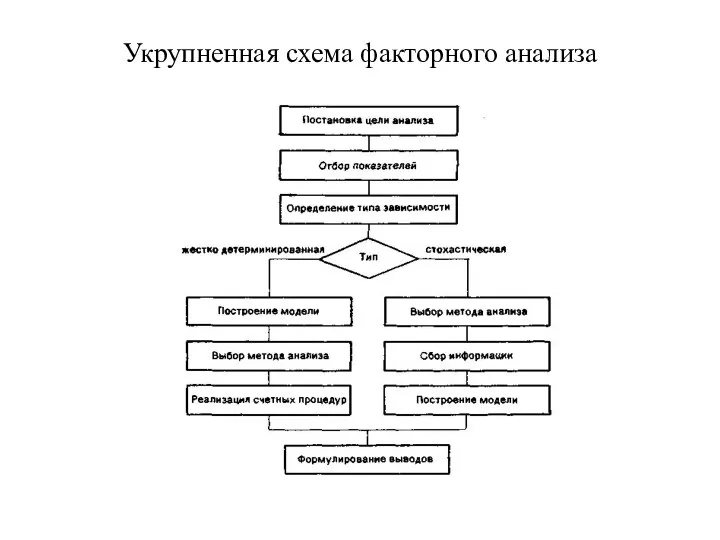
Укрупненная схема факторного анализа

2. Детерминированные модели факторного анализа
Особенности:
Мо­дель полностью замыкается на ту систему факторов, которые поддаются объединению в данную модель. Границей составле­ния такой модели является длина непрерывной цепи прямых связей.
Данный подход не позволяет разделить резуль­таты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели. Таким образом, ис­следователь условно абстрагируется от действия других факто­ров, а все изменения результативного показателя полностью приписываются влиянию факторов, включенных в модель.
Детерминированный анализ может выполняться для единичного объекта в отсутствие совокупности наблюдений.

Модели детерминированного анализа

Последовательность выполняемых процедур при детерминированном факторном анализе:
построение экономически обоснованной (с позиции фактор­ного анализа) детерминированной факторной модели;
выбор приема факторного анализа и подготовка условий для его выполнения;
реализация счетных процедур анализа модели, включая про­верку;
формулирование выводов и рекомендаций по результатам анализа.

Правила построения многофакторных мультипликативных моделей (МММ):
Модель должна быть экономически обоснована, т. е. место фактора в модели должно соответствовать его экономической роли в формировании результативного признака.
Модель целесообразно строить из двухфакторной полной модели путем последовательного расчленения факторов (как пра­вило, качественных) на составляющие; при очередном расшире­нии модели необходимо следить за соблюдением связи «причина — следствие».
Модель должна быть такой, чтобы факторы можно было укрупнять (свертка модели) и слева направо, и справа налево, а произведение двух любых стоящих рядом факторов давало бы экономически понятный фактор более высокого порядка.
Построение неполной модели в большинстве случаев реко­мендуется начинать с построения и последующей легализации соответствующей полной модели.
При написании формулы, факторы в модели рекоме­ндуется располагать в порядке их замены слева направо.

3. Стохастические модели факторного анализа
В факторном анализе эти модели используются по трем основным причинам:
необходимо изучить влияние факторов, по которым нельзя построить жестко детерминированную факторную модель (на­пример, уровень финансового левериджа);
необходимо изучить влияние факторов, которые не поддаются объединению в одной и той же жестко детерминированной модели;
необходимо изучить влияние сложных факторов, которые не могут быть выражены одним количественным показателем (на­пример, уровень инноваций).

Предпосылки реализации стохастического подхода:
а) наличие совокупности;
б) достаточный объем;
в) случайность и независимость наблюдений;
г) однородность. (качественная однородность достигается пу­тем логического отбора; критерием количественной однородно­сти может служить, в частности, коэффициент вариации — его значение не должно превышать 33%);
д) наличие распределения признаков, близкого к нормаль­ному. Существуют различные статистические методы проверки нормальности распределения. Выполнение этого требования в экономических исследованиях нередко сопряжено с существен­ными трудностями и не всегда возможно;
е) наличие специального математического аппарата. В зависи­мости от условий, в которых проводится анализ, могут приме­няться различные методы: регрессионный анализ, ковариацион­ный анализ, спектральный анализ и др.

Построение стохастической модели проводится в несколько этапов:
качественный анализ (постановка цели анализа, определение совокупности, определение результативных и факторных призна­ков, выбор периода и мето­да анализа);
предварительный анализ моделируемой совокупности (про­верка однородности совокупности, исключение аномальных на­блюдений, уточнение необходимого объема выборки, установле­ние законов распределения изучаемых показателей);
построение стохастической (регрессионной) модели (уточне­ние перечня факторов, расчет оценок параметров уравнений ре­грессии, перебор конкурирующих вариантов моделей);
оценка адекватности модели (проверка статистической сущест­венности уравнения в целом и его отдельных параметров, проверка соответствия формальных свойств оценок задачам исследования);
экономическая интерпретация и практическое использование модели (определение пространственно-временной устойчивости построенной зависимости, оценка практических свойств модели).

Типовые задачи детерминированного факторного анализа
1. Оценка влияния относительного изменения факторов на относительное изменение результативного показателя.
Задача имеет смысл для мультипликативных и кратных моде­лей. (простейшую двухфакторную модель р = а * в).
при анализе динамики этих показателей будет выполняться следующее соотношение между индексами:
Iр = Iа * Iв, (1)
где значение индекса находится отношением значения показателя в отчетном периоде к базисному.
Таким образом, относительные изменения факторных и ре­зультативного показателей связаны той же зависимостью, что и показатели в исходной модели.