Содержание
- 2. ЦЕЛИ И ЗАДАЧИ РАБОТЫ Задачи работы: Анализ и практическое освоение известных классических методов и алгоритмов обработки
- 3. Расчет оценок начальных и центральных моментов по выборке независимых наблюдений над случайной величиной 1. Оценки первых
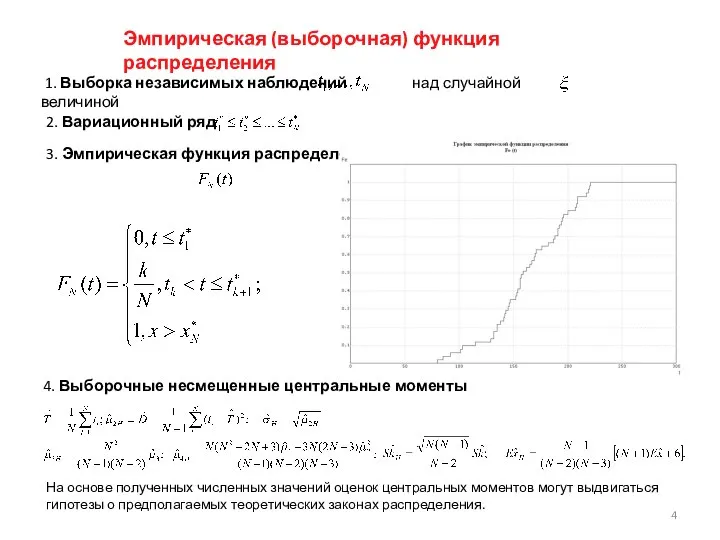
- 4. Эмпирическая (выборочная) функция распределения 1. Выборка независимых наблюдений над случайной величиной 2. Вариационный ряд 3. Эмпирическая
- 5. Метод моментов для точечной оценки неизвестных параметров заданного распределения Метод моментов предложен в 1894 г.. Карлом
- 6. Метод моментов для точечной оценки неизвестных параметров заданного распределения 1. Для нахождения двух неизвестных параметров a
- 7. Метод моментов для точечной оценки неизвестных параметров заданного распределения 2. Для нахождения двух неизвестных параметров a
- 8. Метод максимального правдоподобия для точечной оценки неизвестных параметров заданного распределения Предложен в 1912 г. Рональдом Айлмер
- 9. Для экспоненциального распределения с плотностью вероятности функция правдоподобия имеет вид или . Необходимое условие экстремума при
- 10. Для Гамма – распределения с плотностью вероятности Функция правдоподобия или эквивалентная ей Необходимое условие экстремума: Из
- 11. Для распределения Вейбулла с неизвестных параметров a и b для полной выборки Функция правдоподобия Необходимое условие
- 12. Расчет параметров a и b распределения Вейбулла для цензурированной выборки Функция правдоподобия Необходимое условие экстремума: Метод
- 13. 1. Алгебраическое уравнение для нахождения параметра а распределения Вейбулла при применении ММ Вычислительные трудности решения сложных
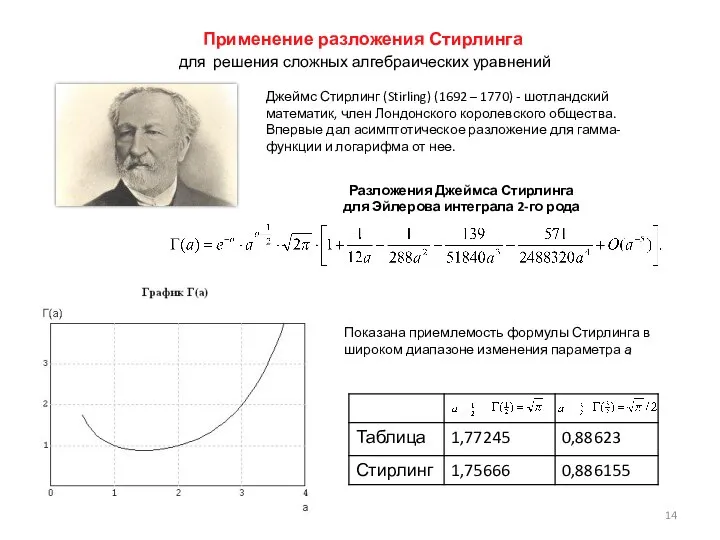
- 14. Применение разложения Стирлинга для решения сложных алгебраических уравнений Джеймс Стирлинг (Stirling) (1692 – 1770) - шотландский
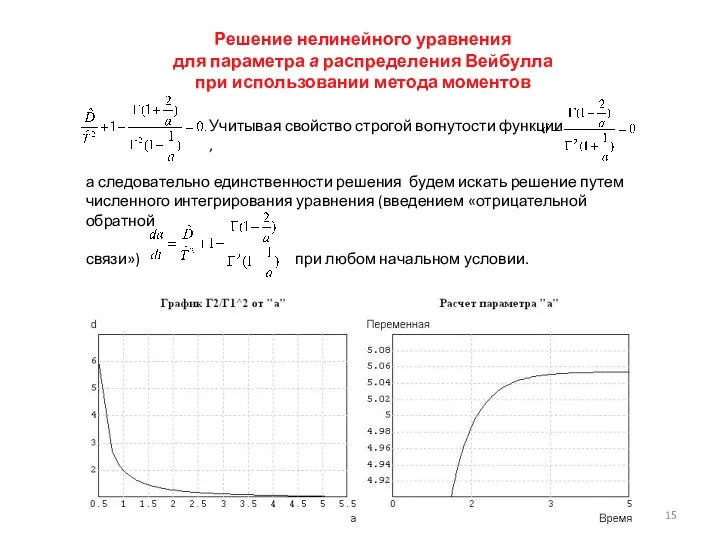
- 15. Решение нелинейного уравнения для параметра а распределения Вейбулла при использовании метода моментов Учитывая свойство строгой вогнутости
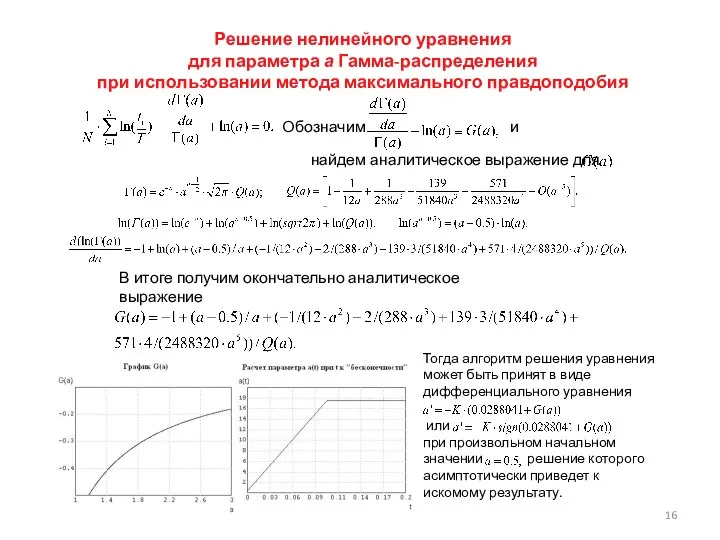
- 16. Решение нелинейного уравнения для параметра а Гамма-распределения при использовании метода максимального правдоподобия В итоге получим окончательно
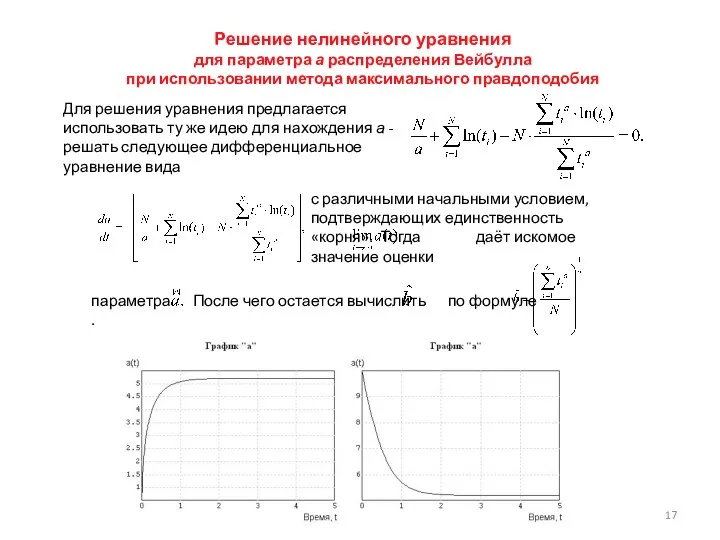
- 17. Решение нелинейного уравнения для параметра а распределения Вейбулла при использовании метода максимального правдоподобия Для решения уравнения
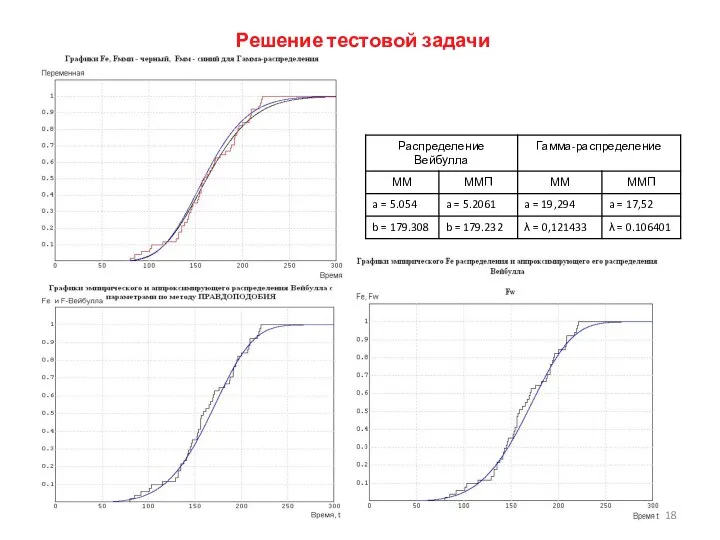
- 18. Решение тестовой задачи
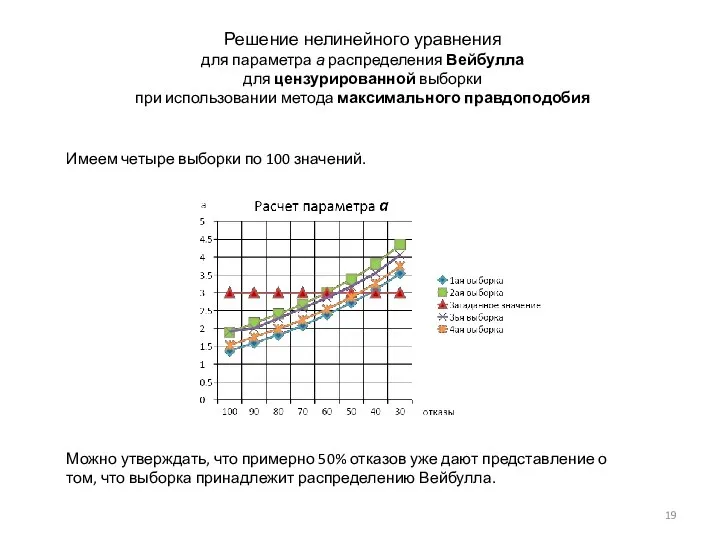
- 19. Решение нелинейного уравнения для параметра а распределения Вейбулла для цензурированной выборки при использовании метода максимального правдоподобия
- 20. Результаты работы 1. Разработано алгоритмическое и программное обеспечение для получения точечных оценок параметров двух практически важных
- 21. Критерии согласия Критерий согласия Колмогорова Критерий “Стареющего” распределения
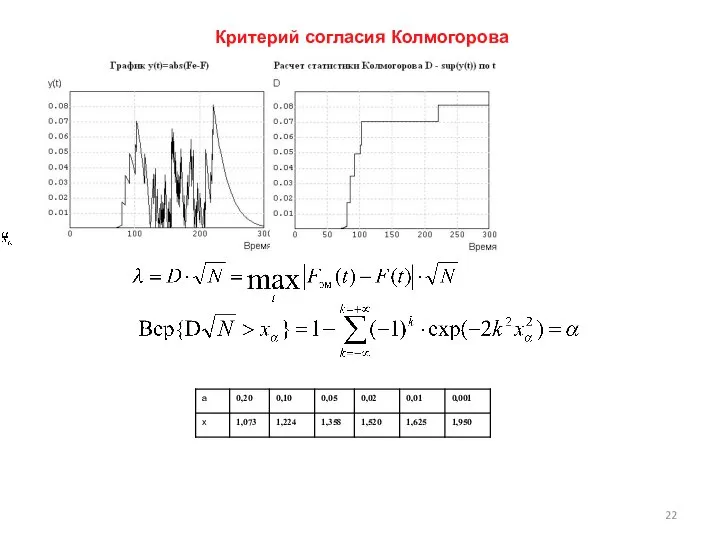
- 22. Критерий согласия Колмогорова
- 23. Очень спасибо за внимание !
- 25. Скачать презентацию














 Урок математики в 1 классе
Урок математики в 1 классе Буквенные выражения
Буквенные выражения Дискретное преобразование Фурье (окончание)
Дискретное преобразование Фурье (окончание) Третий признак подобия треугольников
Третий признак подобия треугольников Линейная регрессия
Линейная регрессия Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Сфера и плоскость
Сфера и плоскость Уравнение. Корень уравнения
Уравнение. Корень уравнения Степень с натуральным показателем и ее свойства. Обобщение. 7 класс
Степень с натуральным показателем и ее свойства. Обобщение. 7 класс Противоположные числа. Устный счет
Противоположные числа. Устный счет Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов Теоремы синусов и косинусов. Тест
Теоремы синусов и косинусов. Тест Справочный материал. 9 класс
Справочный материал. 9 класс Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число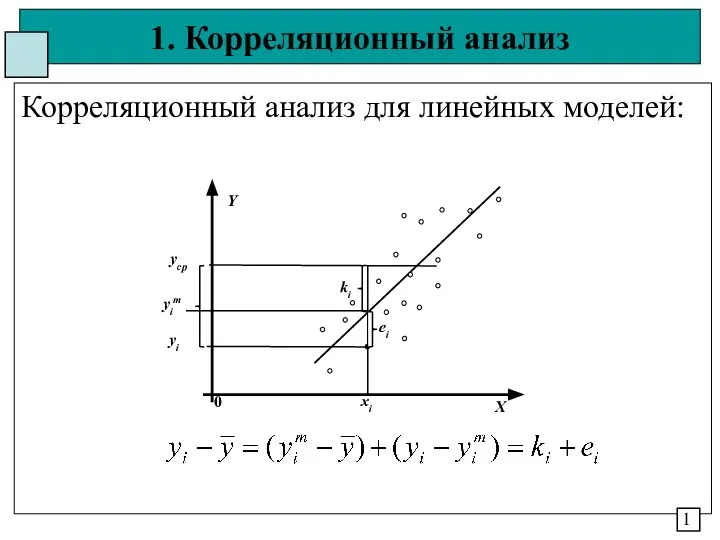 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Подготовка к ГИА по математике. Задания 6
Подготовка к ГИА по математике. Задания 6 Презентация на тему О числах
Презентация на тему О числах  Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)  Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Построение диаграмм и графиков
Построение диаграмм и графиков Тесты по математике
Тесты по математике Геометрическая прогрессия
Геометрическая прогрессия Параллелепипед и куб. 3 класс
Параллелепипед и куб. 3 класс Сумма углов треугольника
Сумма углов треугольника Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла Линии на плоскости
Линии на плоскости