- Главная
- Математика
- Показательная функция

Содержание
Слайд 3Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на
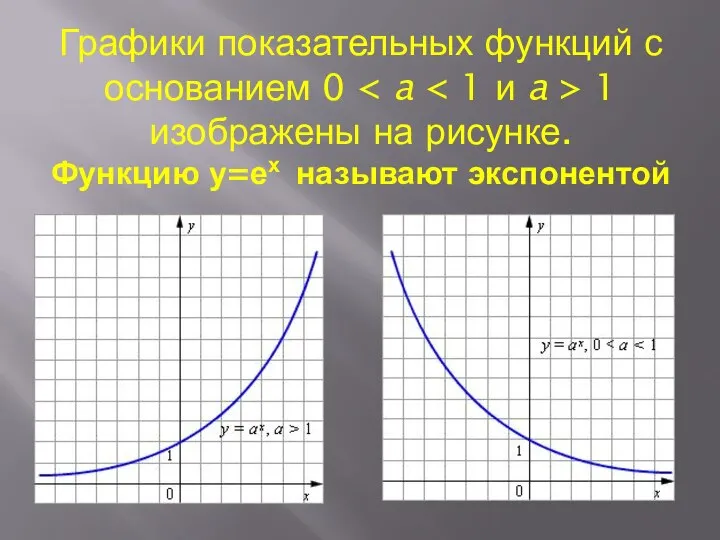
рисунке.
Функцию у=ех называют экспонентой
Слайд 4Основные свойства показательной функции y = a x при a > 1:
Область определения функции - вся числовая прямая.
Область значений
Основные свойства показательной функции y = a x при a > 1:
Область определения функции - вся числовая прямая.
Область значений

функции - промежуток
(0;+ ).
Функция строго возрастает на всей числовой прямой, то есть, если x1< x2 , то ax < ax .
При x = 0 значение функции равно 1.
Если x > 0 , то a x > 1 и если x < 0, то 0 < a x < 1.
(0;+ ).
Функция строго возрастает на всей числовой прямой, то есть, если x1< x2 , то ax < ax .
При x = 0 значение функции равно 1.
Если x > 0 , то a x > 1 и если x < 0, то 0 < a x < 1.
1
2
- Предыдущая
Математика в медицине. Области примененияСледующая -
Функции и графики
 Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА
Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА  Биномиальное распределение
Биномиальное распределение Коллинеарные и неколлинеарные векторы. Разложение вектора по неколлинеарным векторам
Коллинеарные и неколлинеарные векторы. Разложение вектора по неколлинеарным векторам Некоторые методические приемы для работы с детьми ЗПР на уроках математики
Некоторые методические приемы для работы с детьми ЗПР на уроках математики Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Его величество п
Его величество п Понятие площади и свойства (8 класс)
Понятие площади и свойства (8 класс) Презентация на тему Решение простейших тригонометрических неравенств
Презентация на тему Решение простейших тригонометрических неравенств  Аксиома параллельных прямых
Аксиома параллельных прямых Комплексные числа
Комплексные числа Внутренний контроль качества результатов КХА
Внутренний контроль качества результатов КХА Сокращение дробей. Тождество
Сокращение дробей. Тождество Двоичная арифметика
Двоичная арифметика Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними Сложение смешанных дробей
Сложение смешанных дробей Правило отыскания НОД
Правило отыскания НОД Средняя линия треугольника
Средняя линия треугольника L1-1
L1-1 Площадь параллелограмма
Площадь параллелограмма Анализ геометрических высказываний
Анализ геометрических высказываний Доли. Зарядка для ума
Доли. Зарядка для ума Решение дробных рациональных уравнений. Алгебра 8 класс
Решение дробных рациональных уравнений. Алгебра 8 класс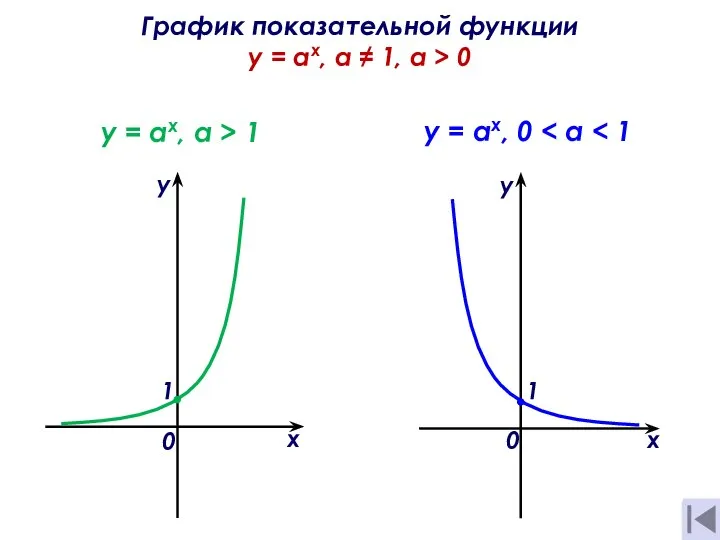 Показательные неравенства и уравнения
Показательные неравенства и уравнения Задания по математике
Задания по математике Дискретная математика. Множества
Дискретная математика. Множества