Содержание
- 2. Что такое граф? Граф — это структура, представляющая собой набор объектов, в котором некоторые пары объектов
- 3. Что такое граф? Например: Вершины (желтые кружки) is V = {1,2,3,4,5} Ребра (черные линии) это пары
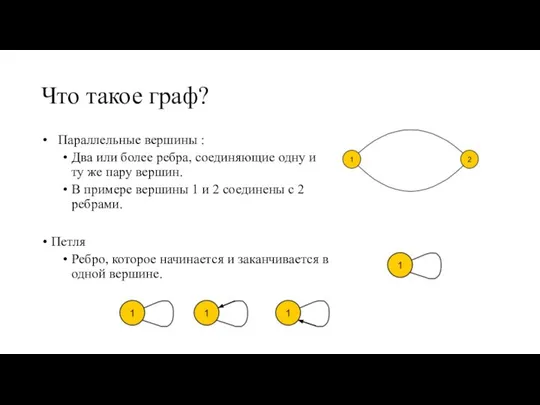
- 4. Что такое граф? Параллельные вершины : Два или более ребра, соединяющие одну и ту же пару
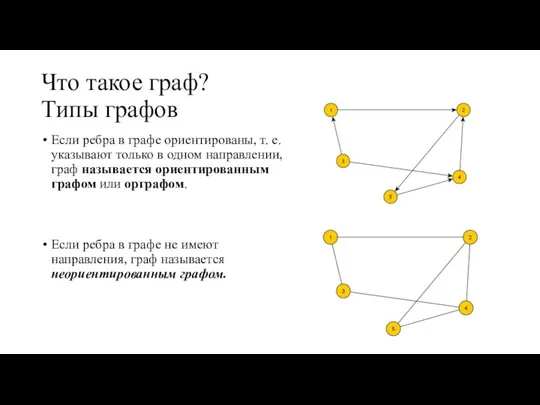
- 5. Что такое граф? Типы графов Если ребра в графе ориентированы, т. е. указывают только в одном
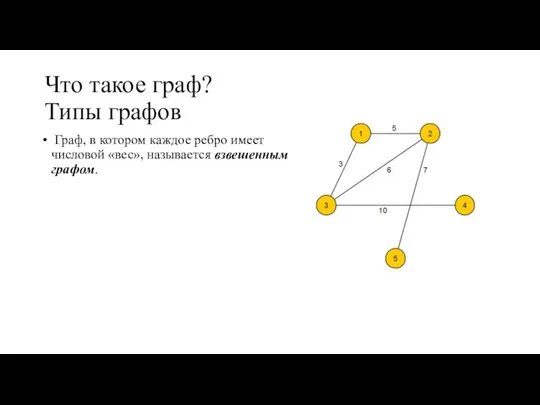
- 6. Граф, в котором каждое ребро имеет числовой «вес», называется взвешенным графом. Что такое граф? Типы графов
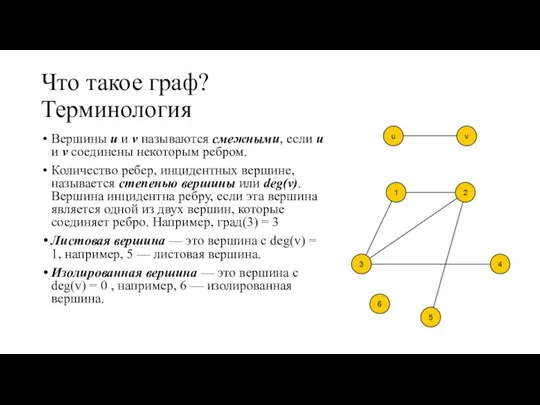
- 7. Что такое граф? Терминология Вершины u и v называются смежными, если u и v соединены некоторым
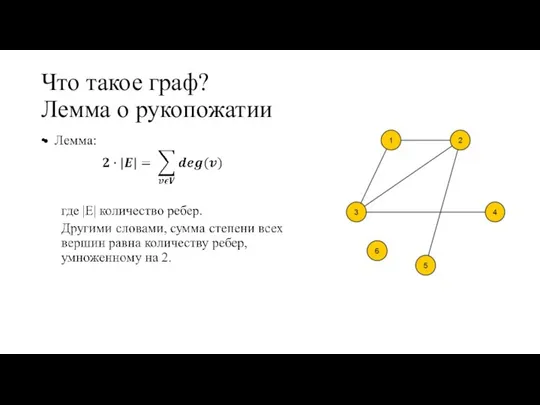
- 8. Что такое граф? Лемма о рукопожатии
- 9. Что такое граф? Терминология
- 10. Графическое представление
- 11. Что такое граф? Представление Нужно представить график в компьютере. 3 обычных вида представления։ Список ребер Матрица
- 12. Что такое граф? Представление. Список ребер Простое перечисление ребер : Для этого примера список узлов {1,
- 13. Что такое граф? Представление: Список смежности
- 14. Что такое граф? Представление։ Матрица смежности Если между вершинами i и j есть ребро, то (i,
- 15. Что такое граф? Представление. Ориентированный граф В случае ориентированного графа представление остается прежним, но ребра добавляются
- 16. Breadth First Search (BFS) Поиск в ширину
- 17. Breadth First Search (BFS) BFS также является методом обхода графа. Алгоритм: BFS(v) { добавить v в
- 18. Breadth First Search (BFS) Посещенные вершины : {} Очередь: {} Текущая вершина : - Легенда: Зеленый
- 19. Breadth First Search (BFS) Посещенные вершины : {} Очередь : {1} Текущая вершина : - 1
- 20. Breadth First Search (BFS) Посещенные вершины : {1} Очередь : {} Текущая вершина : 1 1
- 21. Breadth First Search (BFS) Посещенные вершины : {1} Очередь : {} Текущая вершина : 1 1
- 22. Breadth First Search (BFS) Посещенные вершины : {1} Очередь : {2, 4} Текущая вершина: 1 1
- 23. Breadth First Search (BFS) Посещенные вершины : {1} Очередь : {2, 4} Текущая вершина: 1 1
- 24. Breadth First Search (BFS) Посещенные вершины : {1} Очередь : {2, 4} Текущая вершина: - 1
- 25. Breadth First Search (BFS) Посещенные вершины : {1, 2} Очередь : {4} Текущая вершина : 2
- 26. Breadth First Search (BFS) Посещенные вершины : {1, 2} Очередь : {4} Текущая вершина : 2
- 27. Breadth First Search (BFS) Посещенные вершины : {1, 2} Очередь : {4, 6, 7} Текущая вершина
- 28. Breadth First Search (BFS) Посещенные вершины : {1, 2} Очередь : {4, 6, 7} Текущая вершина
- 29. Breadth First Search (BFS) Посещенные вершины : {1, 2} Очередь : {4, 6, 7} Текущая вершина
- 30. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4} Очередь : {6, 7} Текущая вершина
- 31. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4} Очередь : {6, 7} Текущая вершина:
- 32. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4} Очередь : {6, 7, 5} Текущая
- 33. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4} Очередь : {6, 7, 5} Текущая
- 34. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4} Очередь : {6, 7, 5} Текущая
- 35. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6} Очередь : {7, 5} Текущая
- 36. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6} Очередь : {7, 5} Текущая
- 37. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6} Очередь : {7, 5} Текущая
- 38. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6} Очередь : {7, 5} Текущая
- 39. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7} Очередь : {5} Текущая
- 40. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7} Очередь : {5} Текущая
- 41. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7} Очередь : {5, 3}
- 42. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7} Очередь : {5, 3}
- 43. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7} Очередь : {5, 3}
- 44. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5} Очередь : {3}
- 45. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5} Очередь : {3}
- 46. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5} Очередь : {3,
- 47. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5} Очередь : {3,
- 48. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5} Очередь : {3,
- 49. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3} Очередь :
- 50. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3} Очередь :
- 51. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3} Очередь :
- 52. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3} Очередь :
- 53. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3, 8} Очередь
- 54. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3, 8} Очередь
- 55. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3, 8} Очередь
- 56. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3, 8} Очередь
- 57. Breadth First Search (BFS) Посещенные вершины : {1, 2, 4, 6, 7, 5, 3, 8} Очередь
- 58. Breadth First Search (BFS)
- 59. Depth First Search (DFS) Поиск в глубину
- 60. Depth First Search (DFS) Посещенные вершины : {} Стек: {} Текущая вершина : - Легенда: Зеленый
- 61. Depth First Search (DFS) Посещенные вершины : {} Стек : {1} Текущая вершина : - 1
- 62. Depth First Search (DFS) Посещенные вершины : {1} Стек : {} Текущая вершина : 1 1
- 63. Depth First Search (DFS) Посещенные вершины : {1} Стек : {} Текущая вершина : 1 1
- 64. Depth First Search (DFS) Посещенные вершины : {1} Стек : {2, 4} Текущая вершина: 1 1
- 65. Depth First Search (DFS) Посещенные вершины : {1} Cтек : {2, 4} Текущая вершина: 1 1
- 66. Depth First Search (DFS) Посещенные вершины : {1} Стек : {2, 4} Текущая вершина: - 1
- 67. Depth First Search (DFS) Посещенные вершины : {1, 2} Стек : {4} Текущая вершина : 2
- 68. Depth First Search (DFS) Посещенные вершины : {1, 2} Стек : {6, 7, 4} Текущая вершина
- 69. Depth First Search (DFS) Посещенные вершины : {1, 2} Стек : {6, 7, 4} Текущая вершина
- 70. Depth First Search (DFS) Посещенные вершины : {1, 2} Стек : {6, 7, 4} Текущая вершина
- 71. Depth First Search (DFS) Посещенные вершины : {1, 2} Стек : {6, 7, 4} Текущая вершина
- 72. Depth First Search (DFS) Посещенные вершины : {1, 2, 6} Стек : {7, 4} Текущая вершина
- 73. Depth First Search (DFS) Посещенные вершины : {1, 2, 6, 7} Стек : {3, 4} Текущая
- 74. Depth First Search (DFS) Посещенные вершины : {1, 2, 6, 7, 3} Стек : {4} Текущая
- 75. Depth First Search (DFS) Посещенные вершины : {1, 2, 6, 7, 3, 4} Стек : {5}
- 76. Depth First Search (DFS) Посещенные вершины : {1, 2, 6, 7, 3, 4, 5} Стек :
- 77. Depth First Search (DFS) Посещенные вершины : {1, 2, 6, 7, 3, 4, 5} Стек :
- 78. Depth First Search (DFS) Посещенные вершины : {1, 2, 6, 7, 3, 4, 5, 8} Очередь
- 79. Depth First Search (DFS)
- 80. Алгоритм Дейкстры
- 81. Э́дсгер Ви́бе Де́йкстра (11.05.1930— 6.08.2002) — нидерландский учёный, труды которого оказали влияние на развитие информатики и
- 82. Выбрать начальную вершину, присвоить стоимость пути до нее – 0, остальным вершинам ∞; Все вершины являются
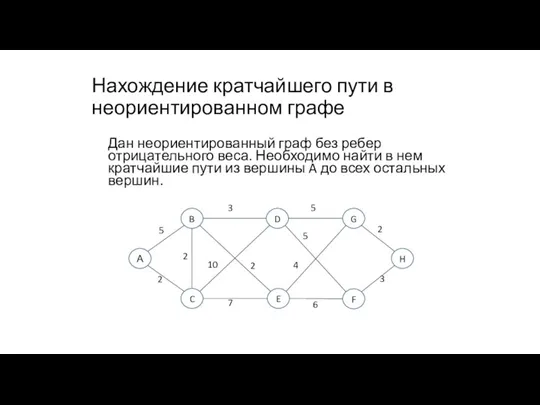
- 83. Нахождение кратчайшего пути в неориентированном графе Дан неориентированный граф без ребер отрицательного веса. Необходимо найти в
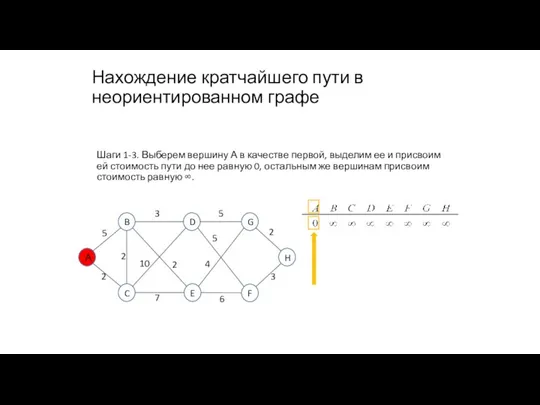
- 84. Нахождение кратчайшего пути в неориентированном графе Шаги 1-3. Выберем вершину А в качестве первой, выделим ее
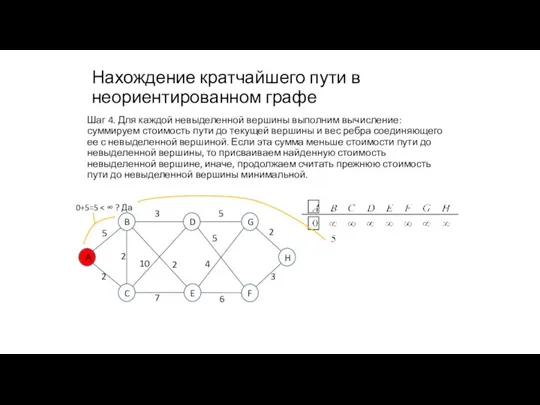
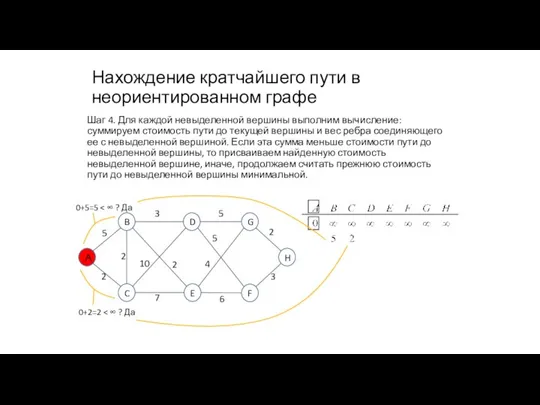
- 85. Нахождение кратчайшего пути в неориентированном графе Шаг 4. Для каждой невыделенной вершины выполним вычисление: суммируем стоимость
- 86. Нахождение кратчайшего пути в неориентированном графе Шаг 4. Для каждой невыделенной вершины выполним вычисление: суммируем стоимость
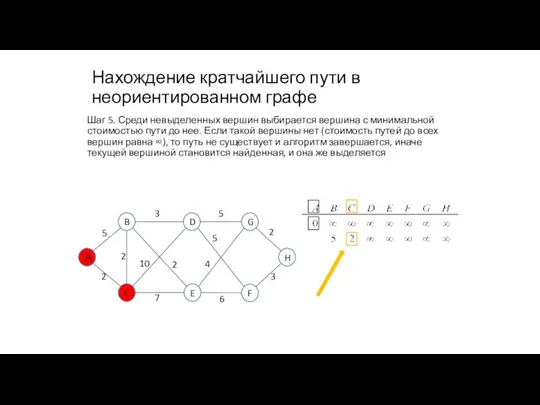
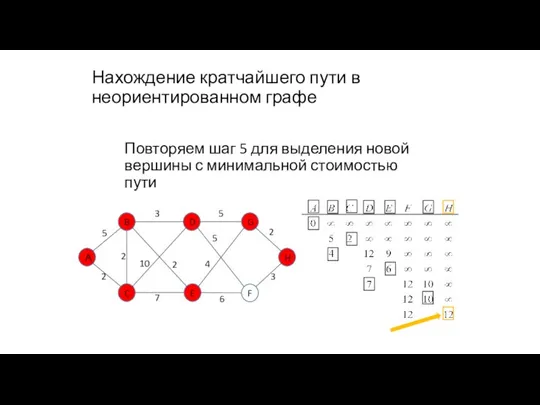
- 87. Нахождение кратчайшего пути в неориентированном графе Шаг 5. Среди невыделенных вершин выбирается вершина с минимальной стоимостью
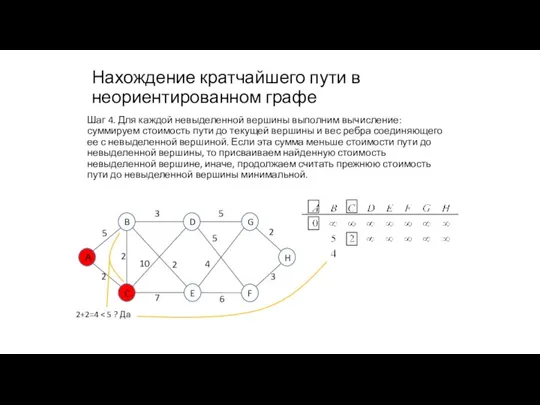
- 88. Нахождение кратчайшего пути в неориентированном графе 2+2=4 Шаг 4. Для каждой невыделенной вершины выполним вычисление: суммируем
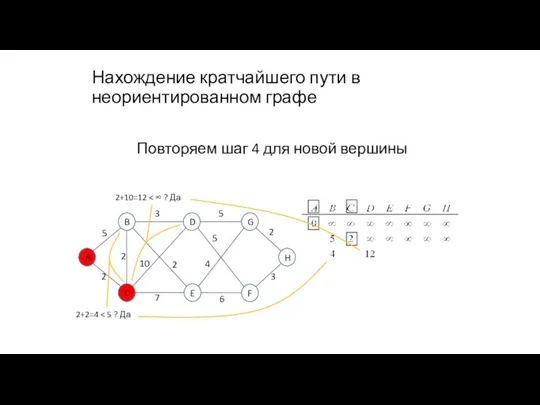
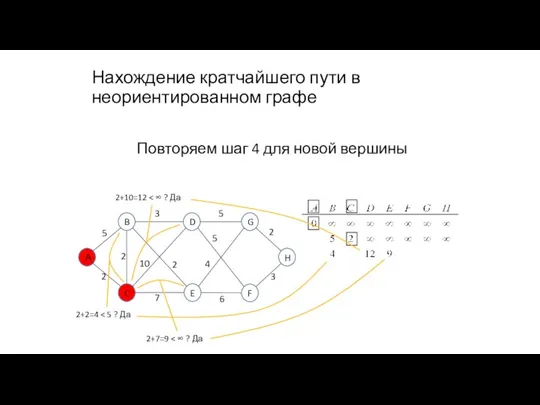
- 89. Нахождение кратчайшего пути в неориентированном графе 2+2=4 Повторяем шаг 4 для новой вершины 2+10=12
- 90. Нахождение кратчайшего пути в неориентированном графе 2+2=4 Повторяем шаг 4 для новой вершины 2+10=12 2+7=9
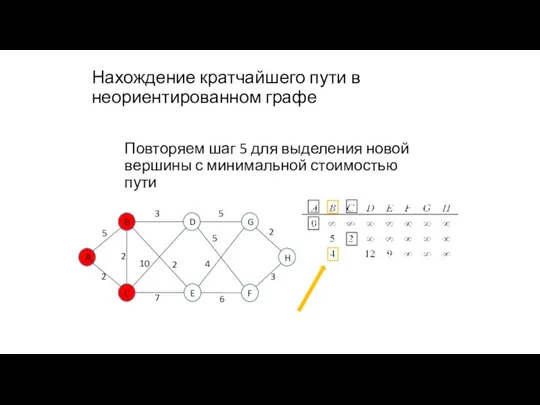
- 91. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 5 для выделения новой вершины с минимальной стоимостью
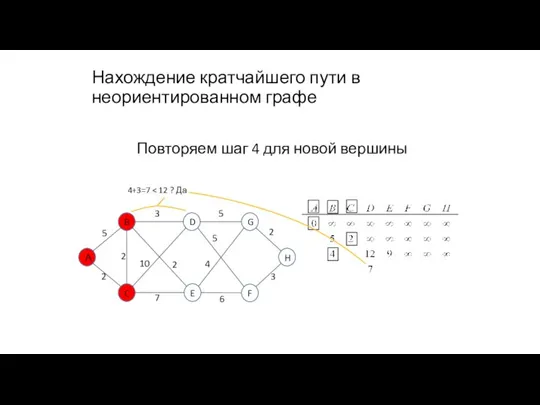
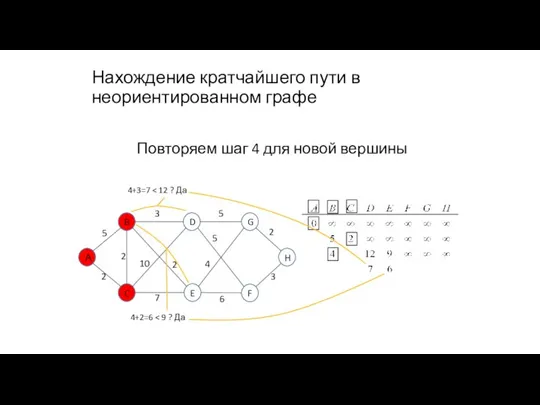
- 92. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 4+3=7
- 93. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 4+3=7 4+2=6
- 94. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 5 для выделения новой вершины с минимальной стоимостью
- 95. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 6+6=12
- 96. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 6+6=12 6+4=10
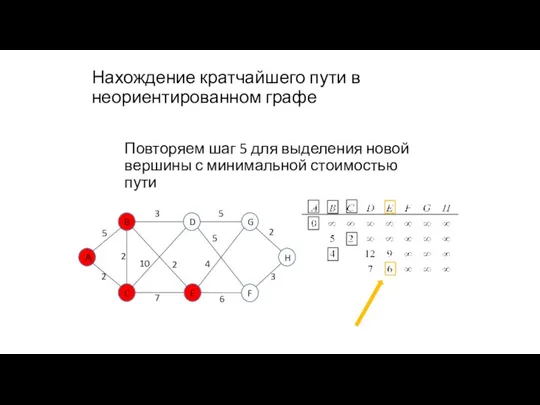
- 97. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 5 для выделения новой вершины с минимальной стоимостью
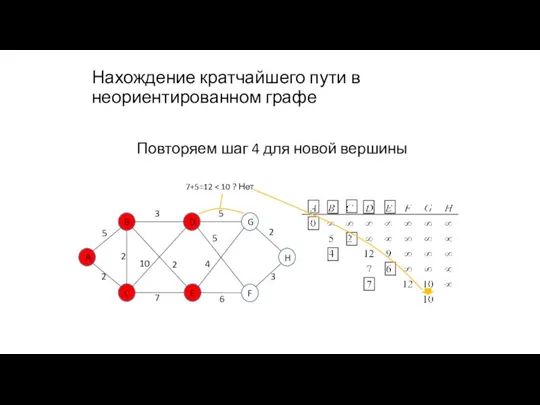
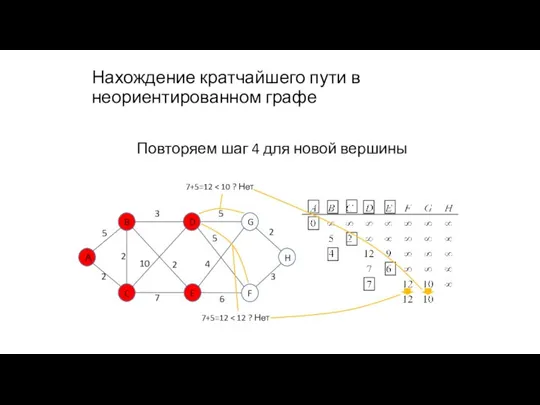
- 98. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 7+5=12
- 99. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 7+5=12 7+5=12
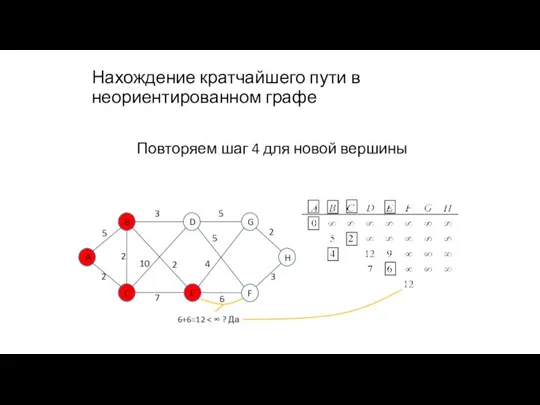
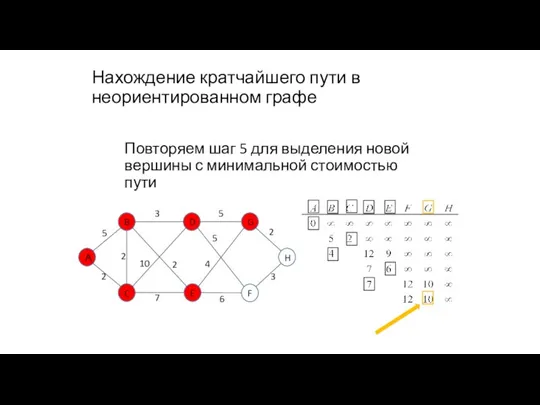
- 100. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 5 для выделения новой вершины с минимальной стоимостью
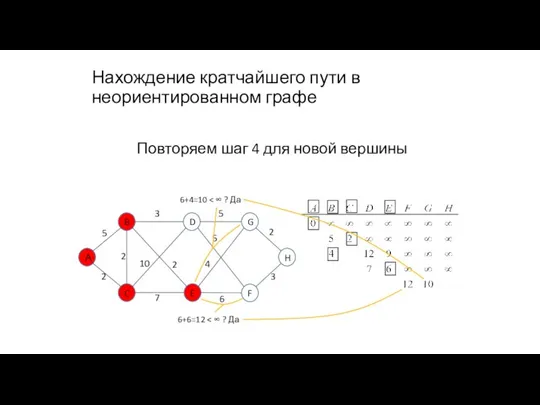
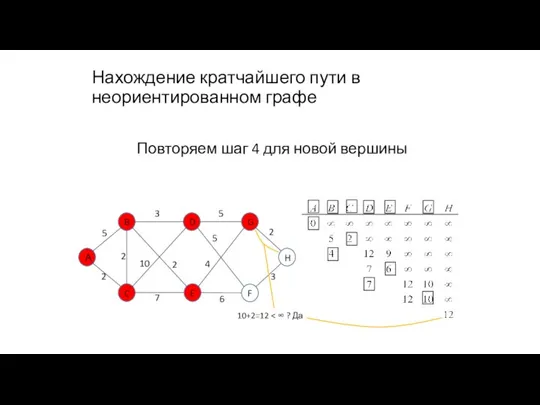
- 101. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 10+2=12
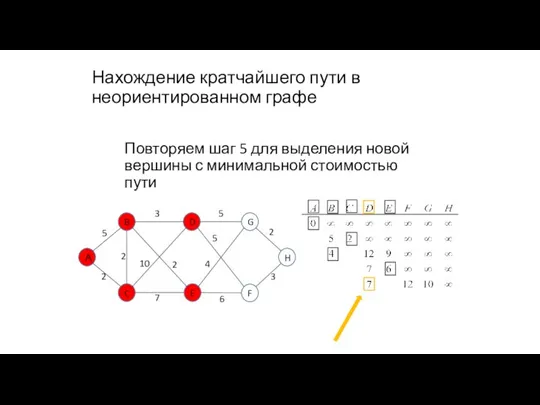
- 102. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 5 для выделения новой вершины с минимальной стоимостью
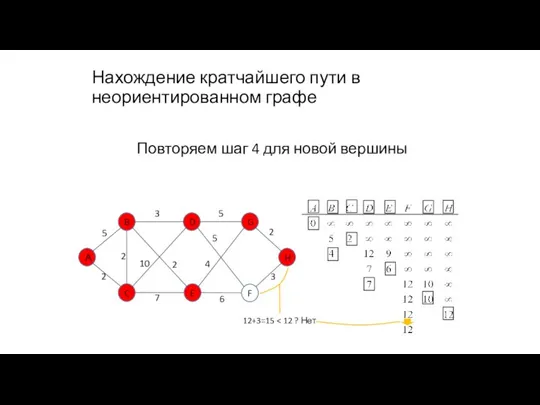
- 103. Нахождение кратчайшего пути в неориентированном графе Повторяем шаг 4 для новой вершины 12+3=15
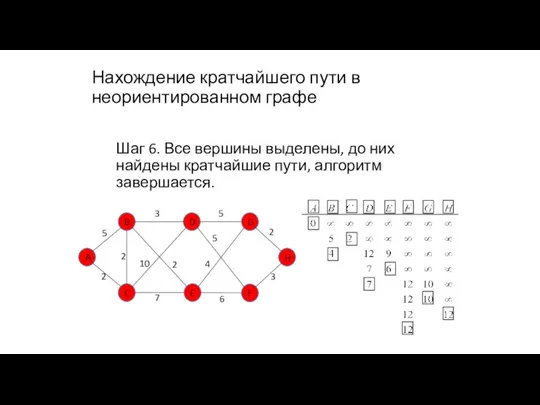
- 104. Нахождение кратчайшего пути в неориентированном графе Шаг 6. Все вершины выделены, до них найдены кратчайшие пути,
- 105. Результаты работы алгоритма Были найдены следующие кратчайшие пути: A → A = 0; A → B
- 107. Скачать презентацию













































































 Понятие числовой последованности
Понятие числовой последованности Действительные числа
Действительные числа Алгебра логики
Алгебра логики Понятие десятичной дроби
Понятие десятичной дроби Алгебраические уравнения
Алгебраические уравнения Глобальная динамическая модель Форрестера
Глобальная динамическая модель Форрестера Практикум по теме х2 = а
Практикум по теме х2 = а Повторение.Геометрия(ЕМН) 10 класс
Повторение.Геометрия(ЕМН) 10 класс Презентация на тему Цифра 3
Презентация на тему Цифра 3  Деление окружности на равные части с помощью угольников и циркуля
Деление окружности на равные части с помощью угольников и циркуля Определители второго и третьего порядка
Определители второго и третьего порядка Решение задач по теме треугольники
Решение задач по теме треугольники Перестановки. Размещения
Перестановки. Размещения Площади фигур. 8 класс
Площади фигур. 8 класс Аксиомы стереометрии
Аксиомы стереометрии Презентация на тему Итоговый тест по математике для 1 класса
Презентация на тему Итоговый тест по математике для 1 класса  Площадь трапеции
Площадь трапеции Размерные цепи
Размерные цепи Десятичные дроби по-английски. Бинарный урок
Десятичные дроби по-английски. Бинарный урок Построение угла, равного данному
Построение угла, равного данному Конспект занятия по математике для будущих первоклассников
Конспект занятия по математике для будущих первоклассников Статистическая теория радиотехнических систем. Постановка задач и классификация методов приема сигналов. (Лекция 10)
Статистическая теория радиотехнических систем. Постановка задач и классификация методов приема сигналов. (Лекция 10) Стереометрия. Теория
Стереометрия. Теория Проверь свои знания. Игра для девятиклассников
Проверь свои знания. Игра для девятиклассников Физико-математических КВН
Физико-математических КВН Разные задачи. Урок 140
Разные задачи. Урок 140 Логарифмы и их свойства
Логарифмы и их свойства Сложение смешанных дробей
Сложение смешанных дробей