Содержание
- 2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №1 Биссектриса внутреннего угла треугольника - отрезок прямой, делящей данный угол на две равные
- 3. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №2 В прямоугольном треугольнике сумма острых углов рана 90о ┐ ɑ β Сумма всех
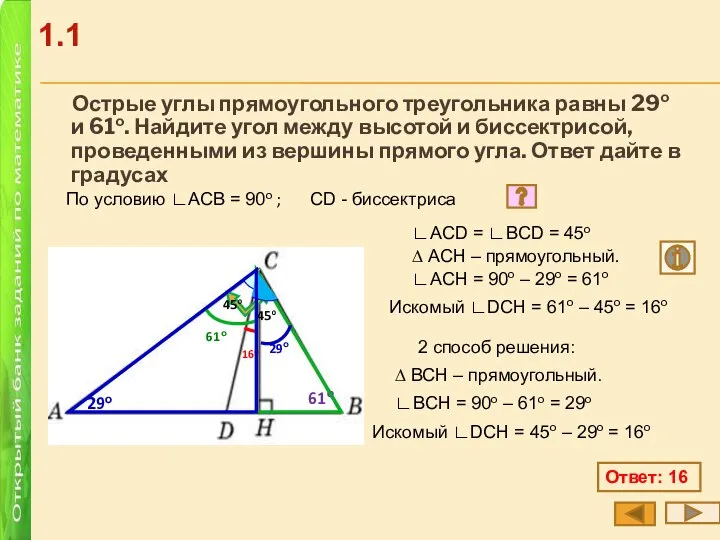
- 4. Острые углы прямоугольного треугольника равны 29о и 61о. Найдите угол между высотой и биссектрисой, проведенными из
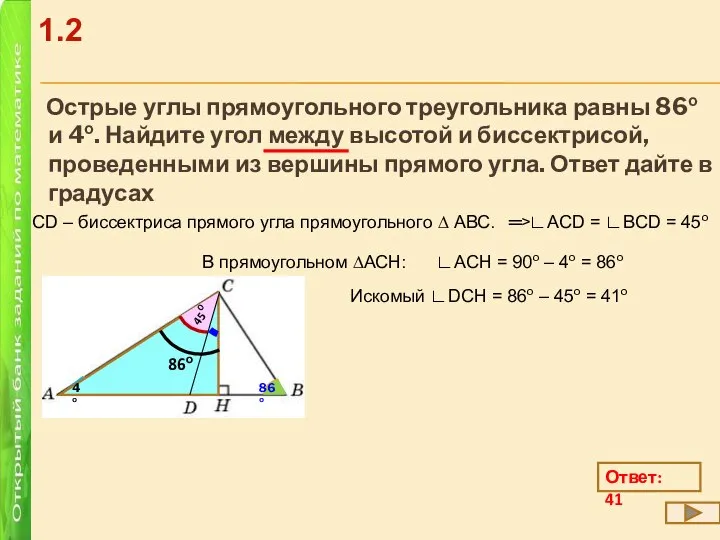
- 5. Острые углы прямоугольного треугольника равны 86о и 4о. Найдите угол между высотой и биссектрисой, проведенными из
- 6. Острые углы прямоугольного треугольника равны 69о и 21о. Найдите угол между высотой и биссектрисой, проведенными из
- 7. Острые углы прямоугольного треугольника равны 53о и 37о. Найдите угол между высотой и биссектрисой, проведенными из
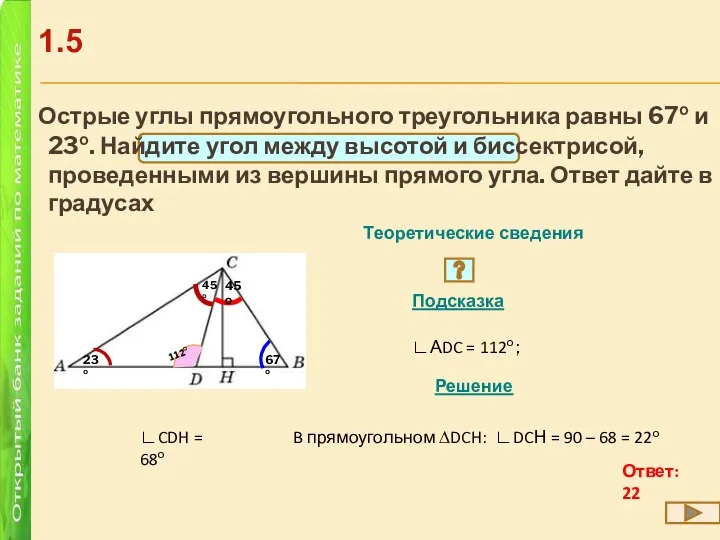
- 8. Острые углы прямоугольного треугольника равны 67о и 23о. Найдите угол между высотой и биссектрисой, проведенными из
- 10. Скачать презентацию




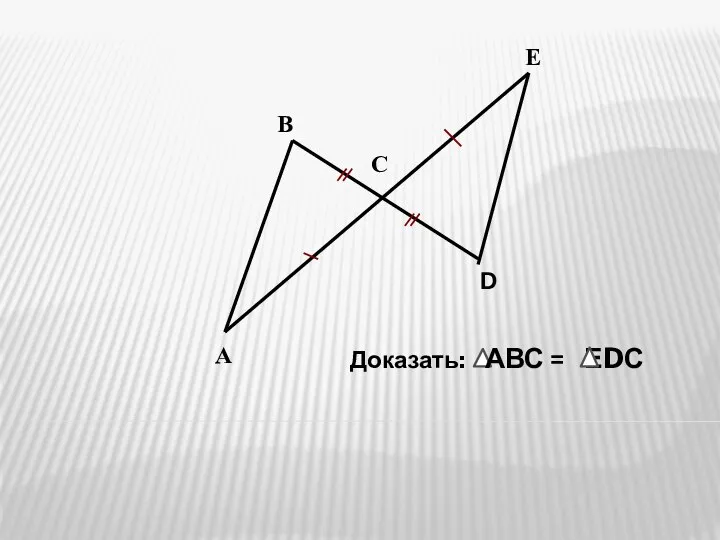 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Нахождение производных функций
Нахождение производных функций Линейная функция и её график
Линейная функция и её график Метрическая система мер
Метрическая система мер Параллельность_прямых_в_пространстве_2019
Параллельность_прямых_в_пространстве_2019 Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Математическая конференция 6а класса
Математическая конференция 6а класса Перевод величин
Перевод величин Пряма в просторі. Площина
Пряма в просторі. Площина Геометрический и физический смысл производной
Геометрический и физический смысл производной Прямоугольник, ромб, квадрат. Осевая и центральная симметрии
Прямоугольник, ромб, квадрат. Осевая и центральная симметрии Уравнение прямой
Уравнение прямой Основные сведения из геометрии. Правильные шестиугольники
Основные сведения из геометрии. Правильные шестиугольники Функції. Графік функції. 7 клас
Функції. Графік функції. 7 клас Прямое сложение и вычитание
Прямое сложение и вычитание Многогранники. Призма
Многогранники. Призма Приёмы устных вычислений
Приёмы устных вычислений Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Иррациональные неравенства
Иррациональные неравенства Основы математического моделирования социально-экономических процессов
Основы математического моделирования социально-экономических процессов Проценты. 6 класс
Проценты. 6 класс Парная регрессия и корреляция. Тема 2
Парная регрессия и корреляция. Тема 2 Показательная функция. Её свойства
Показательная функция. Её свойства Геометрия вокруг нас
Геометрия вокруг нас Умножение и деления дробей
Умножение и деления дробей Умножение
Умножение Математика. 2 класс
Математика. 2 класс История системы мер длины (часть 2)
История системы мер длины (часть 2)