Слайд 2Метод простой итерации
Рассмотрим уравнение вида х=f(х) с корнем t, отделенным на отрезке

[а;b].
Функция f предполагается непрерывной на этом отрезке.
Уравнение можно получить из исходного уравнения: f(x) = 0 путем эквивалентных преобразований.
Слайд 3Метод простой итерации
Пример.
Уравнение х3–3х+1=0 представляется в виде х=f(х) разными способами. Например:

Слайд 4Метод простой итерации
Метод простой итерации является одним из наиболее удобных и эффективных

методов приближенного решения уравнений. Он основан на многократном применении итерационной формулы xn+1=f(xn) до тех пор, пока соблюдается условие |xn+1–xn| ≥ e, где e — заданная погрешность вычисления корня.
Итерационный процесс сходится (т. е. xn→t при n→∞), если соблюдается условие f'(x)<1 на отрезке [a;b].
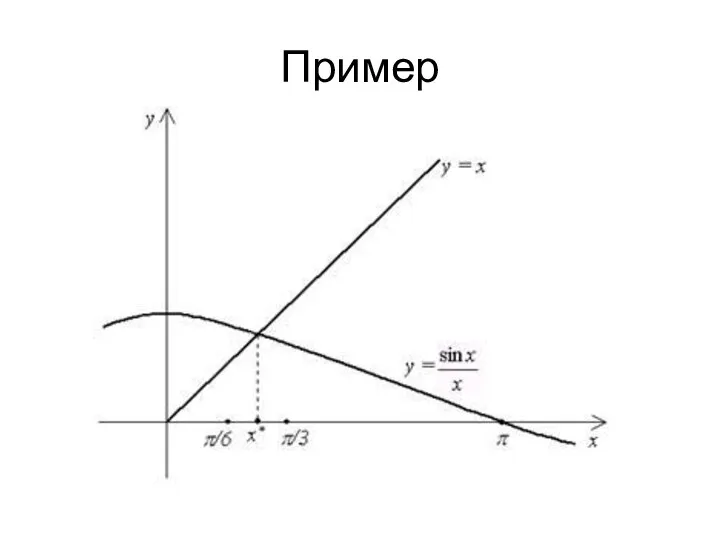
Слайд 5Пример
Используем метод простой итерации для решения уравнения
с точностью
Преобразуем уравнение к виду:

Слайд 6Пример
Нетрудно убедиться, что корень уравнения находится на отрезке
Вычислив значения f(x) на концах отрезка, получим:
т.

е. функция на концах отрезка имеет разные знаки, поэтому внутри отрезка есть корень.
Слайд 8Пример
Подсчитаем первую и вторую производные функции
Так как на отрезке
то производная монотонно возрастает

на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке
Слайд 9Пример
Поэтому справедлива оценка:
Таким образом, условие выполнено,
и можно воспользоваться критерием окончания вычислений.

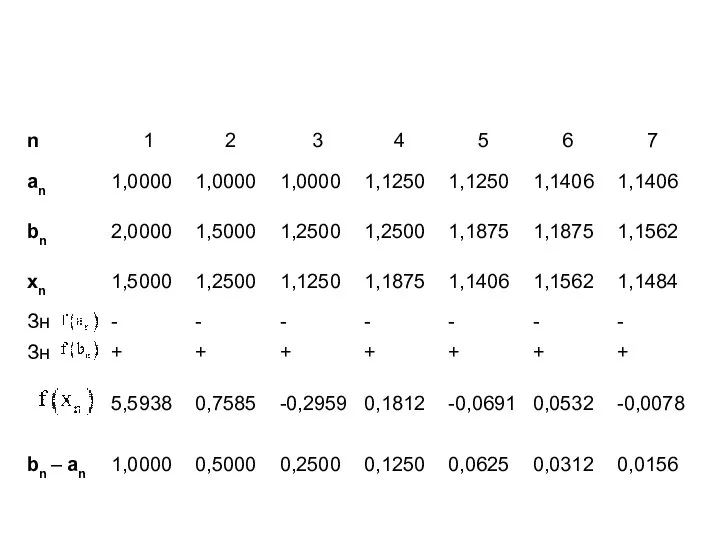
Слайд 10Пример
В таблице приведены приближения, полученные по расчетной формуле.
В качестве начального приближения

выбрано значение
Слайд 11Пример
Критерий окончания выполняется при n=5
Приближенное значение корня с требуемой точностью

Слайд 12Пример 2.
Решить методом простой итерации уравнение на отрезке
с точностью 0,025.
Для

решения исходное уравнение приводится к виду
Для выбора величины λ используем формулу
Тогда расчетная формула имеет вид
Слайд 13Пример 2.
В качестве начального приближения можно выбрать верхнюю границу заданного отрезка
Так как,

то
Слайд 14Задания
1. Отделите корни уравнения 3cos x=x+1.
2. Составьте программу, реализующую метод простой итерации,

и уточните корень уравнения x–sinx–0,25=0 на отрезке [1,1;1,2] с точностью до 0,001.
Слайд 15Метод деления отрезка пополам (метод дихотомии)
Пусть корень t отделен на отрезке [а;b].

Требуется найти приближенное значение корня с точностью до e. Функция f непрерывна на [а;b] и имеет разные знаки в точках a и b (для определенности примем f(a)>0).
Слайд 16Метод деления отрезка пополам (метод дихотомии)
Метод деления отрезка пополам реализуется следующим алгоритмом:
1.

Находим xi=(a+b)/2.
2. Вычисляем f(xi).
3. Если f(xi)>0, задаем a=x, иначе b=x.
4. Проверяем условие b–a > e. Если оно выполняется, идем к п.1, если не выполняется, заканчиваем вычисления и считаем, что t=xi с заданной точностью e.
Слайд 17Метод деления отрезка пополам (метод дихотомии)
Число итераций при использовании этого метода
значительно, и

поэтому сходимость его медленная. Однако при любой ширине отрезка [а;b] сходимость гарантирована. Кроме того метод половинного деления дает простой и удобный алгоритм уточнения корней с любой наперед заданной степенью точности. Он требует от функции f выполнения легко проверяемых свойств: непрерывности на отрезке изоляции корня и разных знаков значений на его концах.
Слайд 18Метод деления отрезка пополам (метод дихотомии)
Пример.
Единственный корень t уравнения х3–х–1=0 расположен на

отрезке [1;2] (проверьте графически!). Необходимо уточнить t с заданной точностью a=0,001. Можно применить метод половинного деления, поскольку функция f(x)=х3–х–1 непрерывна на этом отрезке и на его концах принимает значения разных знаков: f(1) = –1 < 0, f(2)=5> 0.
Слайд 19Пример.
Найдем приближенно с точностью
Эта задача эквивалентна решению уравнения или нахождению нуля функции
В

качестве начального отрезка возьмем отрезок .
Слайд 20Пример.
На концах этого отрезка функция принимает значения с разными знаками:
Найдем число n делений отрезка [1,

2], необходимых для достижения требуемой точности. Имеем:
Слайд 21Пример
Следовательно, не позднее 6-го деления найдем с требуемой точностью,
Результаты вычислений представлены в

таблице



















 Дроби
Дроби Второй признак равенства треугольников. Геометрия , 7 класс
Второй признак равенства треугольников. Геометрия , 7 класс Сжатие(растяжение) графика вдоль оси ординат
Сжатие(растяжение) графика вдоль оси ординат Решите неравенства
Решите неравенства Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби סדר פעולות החשבון
סדר פעולות החשבון Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Уравнения и неравенства с параметрами. 11 класс
Уравнения и неравенства с параметрами. 11 класс Классы интегрируемых функций
Классы интегрируемых функций Гипотеза Пуанкаре
Гипотеза Пуанкаре Diskretnaya_matematika_sootvetstvia
Diskretnaya_matematika_sootvetstvia Решение систем уравнений
Решение систем уравнений Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Системы уравнений
Системы уравнений Три кота. Прибавление и вычитание числа 2
Три кота. Прибавление и вычитание числа 2 Множества. 8 класс
Множества. 8 класс Презентация на тему Устный счёт 1 класс
Презентация на тему Устный счёт 1 класс  Прогрессии
Прогрессии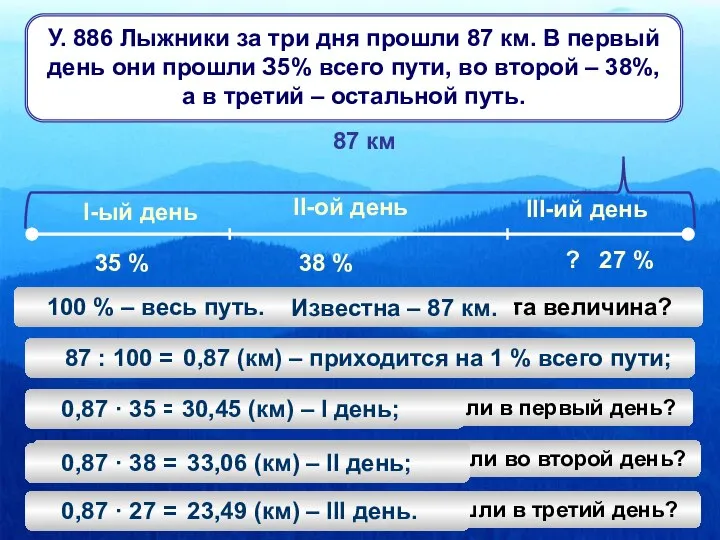 Задачи о лыжниках
Задачи о лыжниках Первообразная. Таблица для нахождения первообразных элементарных функций
Первообразная. Таблица для нахождения первообразных элементарных функций 2 погрешности ру с
2 погрешности ру с Многоэтажные дроби. 8 класс
Многоэтажные дроби. 8 класс Мастер-класс в рамках игры физико-математические забавы
Мастер-класс в рамках игры физико-математические забавы Десятичные дроби
Десятичные дроби Теория вероятностей. Случайные события
Теория вероятностей. Случайные события Построение кривой времени t=f(s) методом инженера Лебедева
Построение кривой времени t=f(s) методом инженера Лебедева Формулы приведения
Формулы приведения Собирательные числительные
Собирательные числительные