Содержание
- 2. Źródło: B. Pańczyk E. Łukasik J. Sikora T. Guziak Metody Numeryczne w przykładach Wydawca: Politechnika Lubelska
- 3. Treść wykładu Aproksymacja Aproksymacja średniokwadratowa. Całkowanie numeryczne (kwadratury interpolacyjne).
- 4. Aproksymacja Aproksymacja (łac. approximare – przybliżać) – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które
- 5. Aproksymacja
- 6. Aproksymacja
- 7. Aproksymacja
- 8. Aproksymacja
- 9. Aproksymacja
- 10. Aproksymacja
- 11. Aproksymacja średniokwadratowa
- 12. Aproksymacja średniokwadratowa
- 13. Aproksymacja średniokwadratowa
- 14. Aproksymacja średniokwadratowa
- 15. Aproksymacja średniokwadratowa
- 16. Aproksymacja średniokwadratowa
- 17. Aproksymacja średniokwadratowa
- 18. Aproksymacja średniokwadratowa
- 19. Aproksymacja średniokwadratowa
- 20. Aproksymacja średniokwadratowa
- 21. Aproksymacja średniokwadratowa
- 22. Aproksymacja średniokwadratowa
- 23. Aproksymacja średniokwadratowa
- 24. Aproksymacja średniokwadratowa
- 25. Aproksymacja średniokwadratowa
- 26. Aproksymacja średniokwadratowa
- 27. Aproksymacja średniokwadratowa
- 28. Zadania do samodzielnego rozwiązania
- 29. Całkowanie numeryczne (kwadratury interpolacyjne)
- 30. Całkowanie numeryczne (kwadratury interpolacyjne)
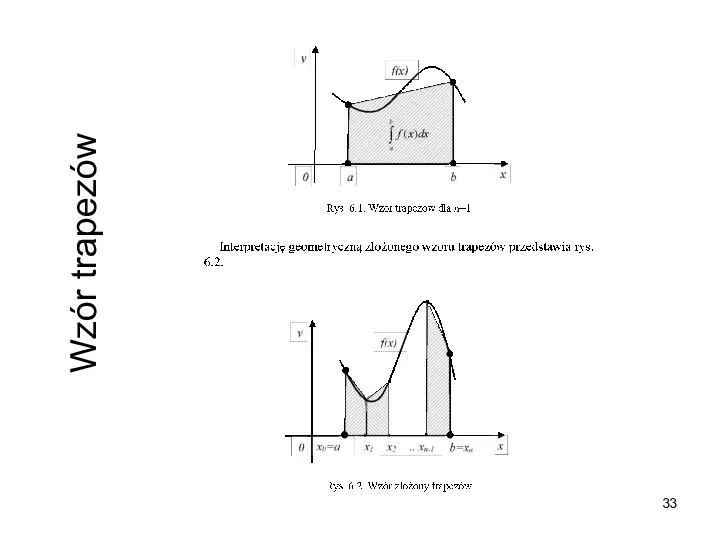
- 31. Wzór trapezów
- 32. Wzór trapezów
- 33. Wzór trapezów
- 34. Wzór trapezów
- 35. Wzór trapezów
- 36. Wzór złożony trapezów
- 37. Wzór Simpsona
- 38. Wzór Simpsona
- 39. Wzór Simpsona
- 40. Wzór Simpsona
- 41. Wzór Simpsona
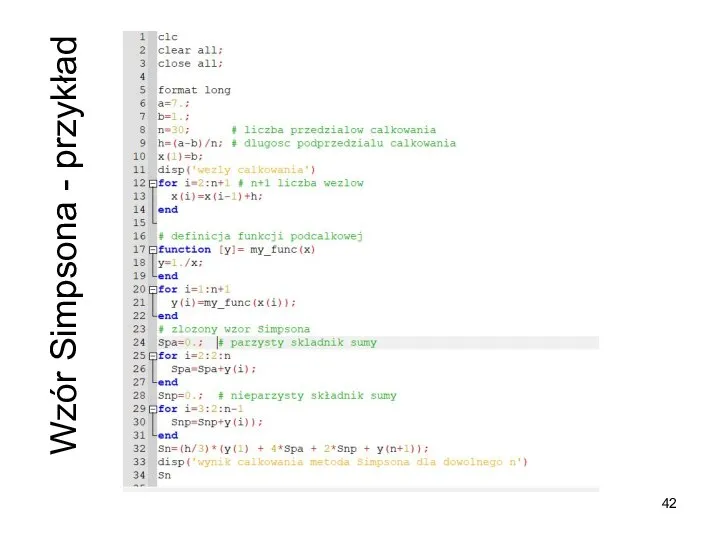
- 42. Wzór Simpsona - przykład
- 43. Wzór Simpsona
- 44. Kwadratury Gaussa Wielomiany ortogonalne – wielomiany wzajemnie do siebie ortogonalne w sensie pewnego iloczynu skalarnego. Korzysta
- 45. Kwadratury Gaussa
- 46. Kwadratury Gaussa
- 47. Kwadratury Gaussa
- 48. Kwadratury Gaussa
- 49. Kwadratury Gaussa
- 50. Kwadratury Gaussa
- 51. Kwadratury Gaussa
- 52. Kwadratury Gaussa
- 53. Kwadratury Gaussa
- 54. Kwadratury Gaussa
- 55. Kwadratury Gaussa
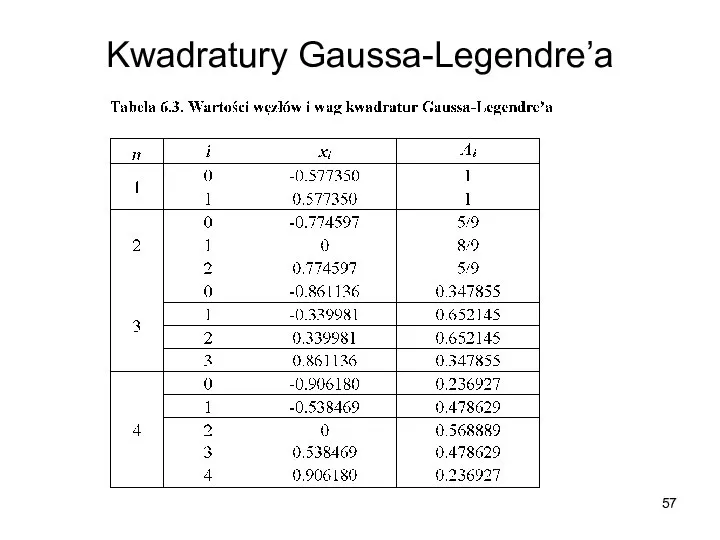
- 56. Kwadratury Gaussa-Legendre’a
- 57. Kwadratury Gaussa-Legendre’a
- 58. Zadania do samodzielnego rozwiązania Wartość całki ze wzoru analitycznego wynosi: -27.51
- 59. Zadania do samodzielnego rozwiązania
- 60. Zadania do samodzielnego rozwiązania
- 61. Zadania do samodzielnego rozwiązania
- 63. Скачать презентацию

























































 Тест на распознавание предметов
Тест на распознавание предметов Брейн-ринг. Геометрия
Брейн-ринг. Геометрия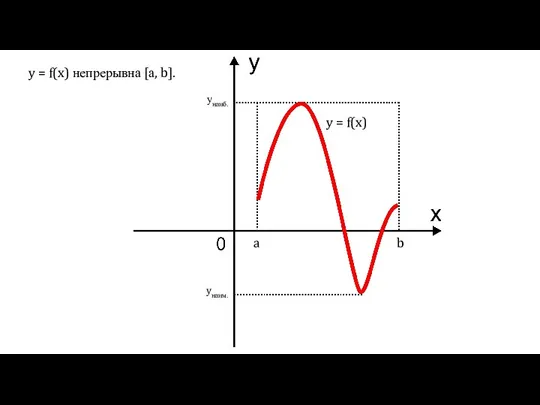 Применение производной
Применение производной Иррациональные неравенства
Иррациональные неравенства Відео. Задача на 2 дії
Відео. Задача на 2 дії Оценка сложных систем в условиях неопределенности
Оценка сложных систем в условиях неопределенности Презентация на тему Графическое решение квадратных уравнений (8 класс)
Презентация на тему Графическое решение квадратных уравнений (8 класс)  Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе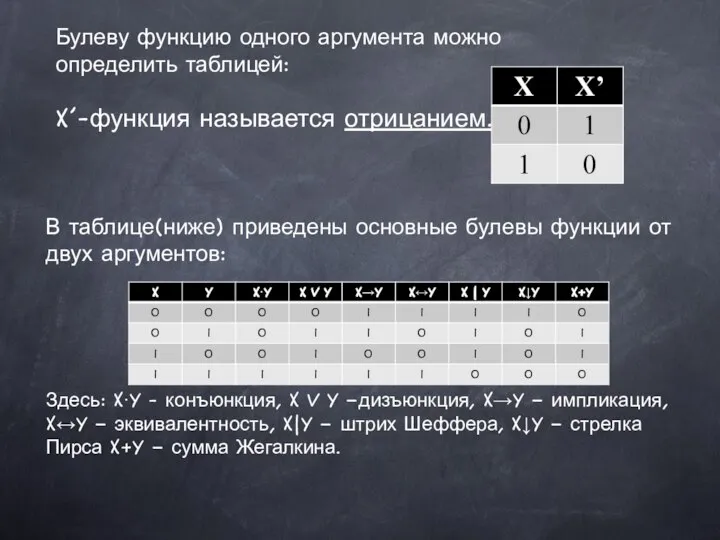 Булевы функции
Булевы функции Математический словарь
Математический словарь Презентация на тему Счет от одного до десяти
Презентация на тему Счет от одного до десяти  Золотое сечение в Web-дизайне
Золотое сечение в Web-дизайне Переменные. Арифметические операции
Переменные. Арифметические операции Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Математика вокруг нас
Математика вокруг нас Граф. Построение графов
Граф. Построение графов ANX.ADJ.DSM.5
ANX.ADJ.DSM.5 Периметр и площадь прямоугольника. Подготовка к контрольной работе
Периметр и площадь прямоугольника. Подготовка к контрольной работе Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Презентация на тему Использование игровых моментов при повторении на уроках математики в 5-ых классах
Презентация на тему Использование игровых моментов при повторении на уроках математики в 5-ых классах  Презентация по математике "Познакомимся с известными математиками" -
Презентация по математике "Познакомимся с известными математиками" -  Наука эконометрика
Наука эконометрика Решение уравнений математической физики методом д’Аламбера
Решение уравнений математической физики методом д’Аламбера Определенный и неопред интеграл. Тема 8
Определенный и неопред интеграл. Тема 8 Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Интерактивный тест. Готовимся к ОГЭ. 2 вариант, задание 8
Интерактивный тест. Готовимся к ОГЭ. 2 вариант, задание 8 Геометрия на каждом уроке
Геометрия на каждом уроке Решение систем линейных уравнений разными методами
Решение систем линейных уравнений разными методами