Содержание
- 2. A B C D E G 1 2 3 4 5 6 7 8 9 П
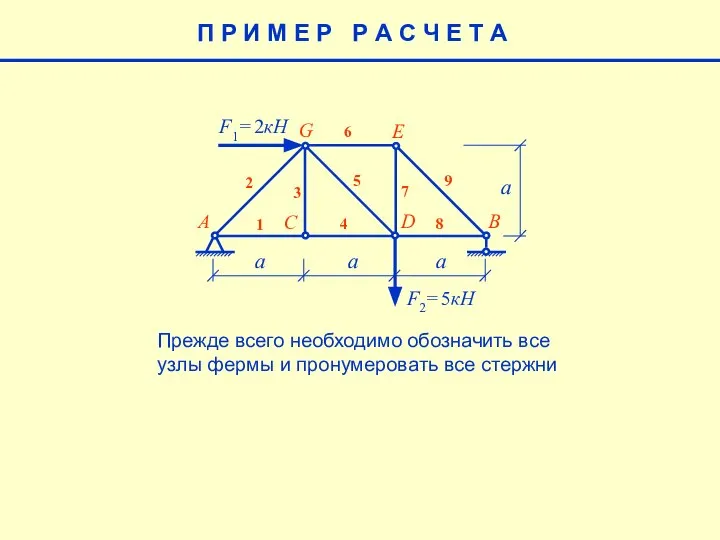
- 3. П Р И М Е Р Р А С Ч Е Т А Полный расчёт фермы,
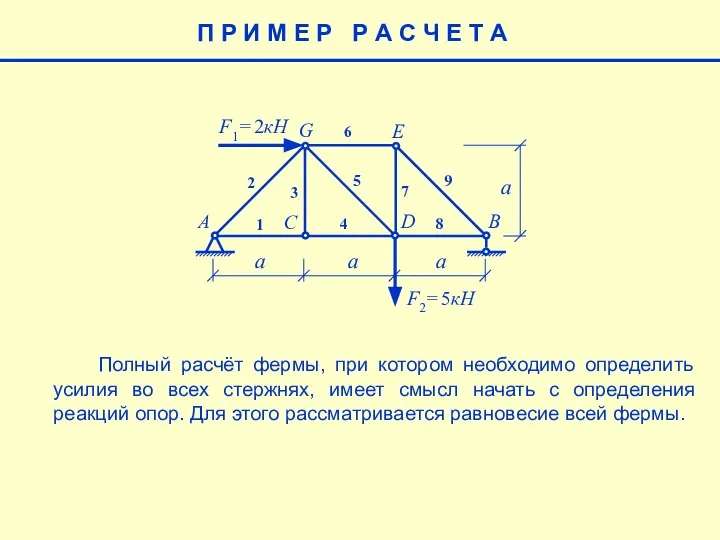
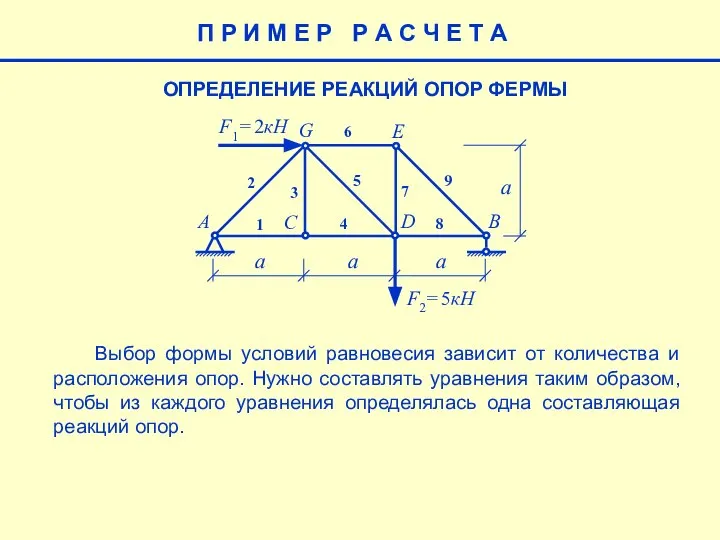
- 4. П Р И М Е Р Р А С Ч Е Т А Выбор формы условий
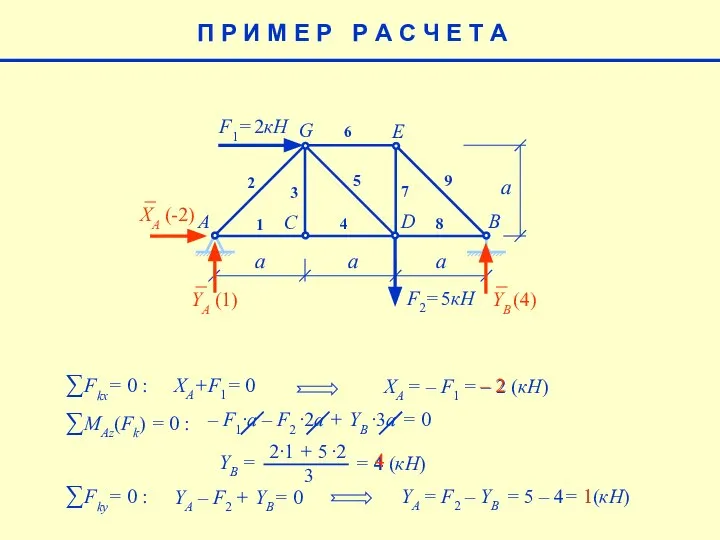
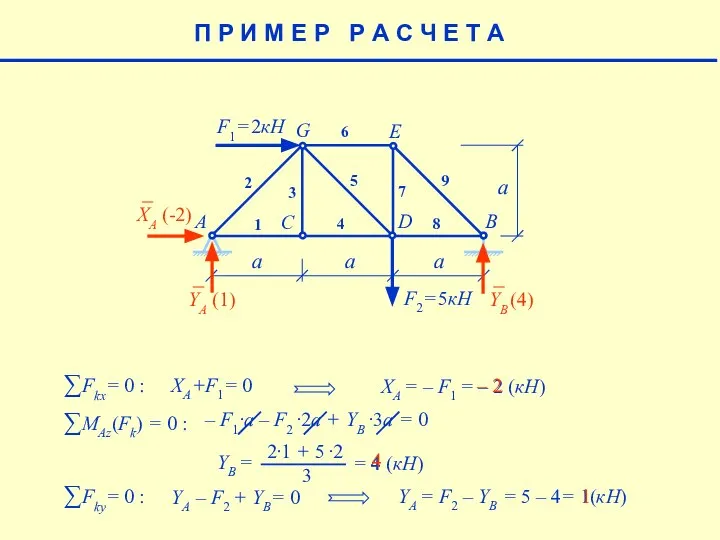
- 5. a F1= 2кН F2= 5кН A B C D E G 1 2 3 4 5
- 6. a F1= 2кН F2= 5кН A B C D E G 1 2 3 4 5
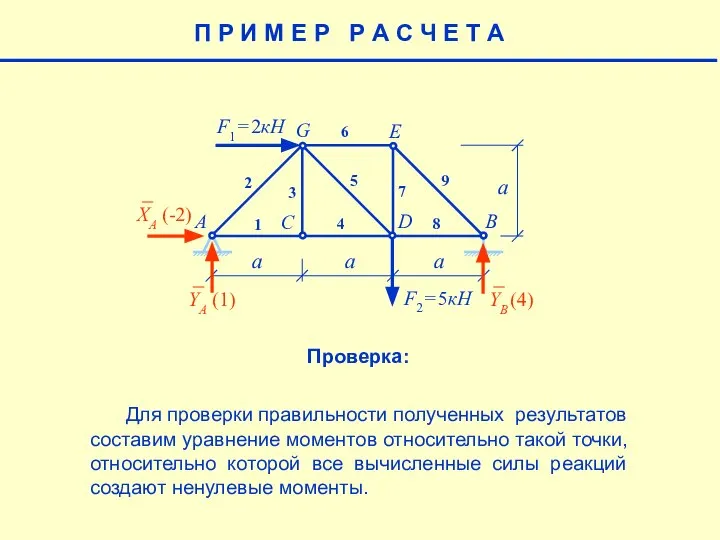
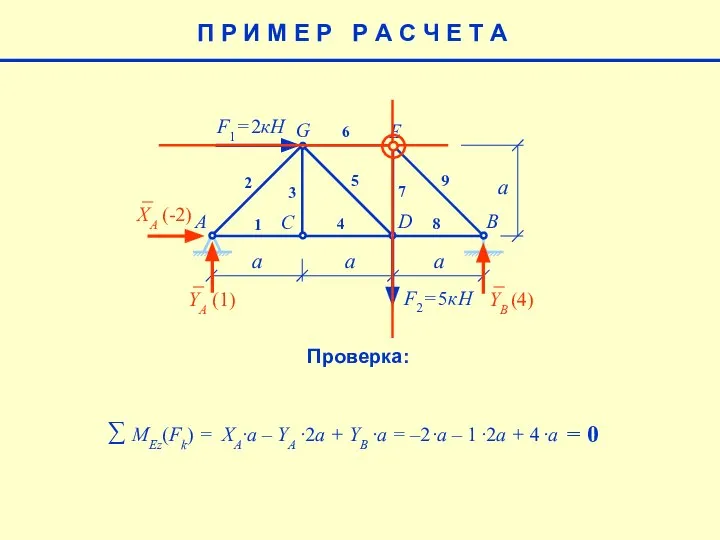
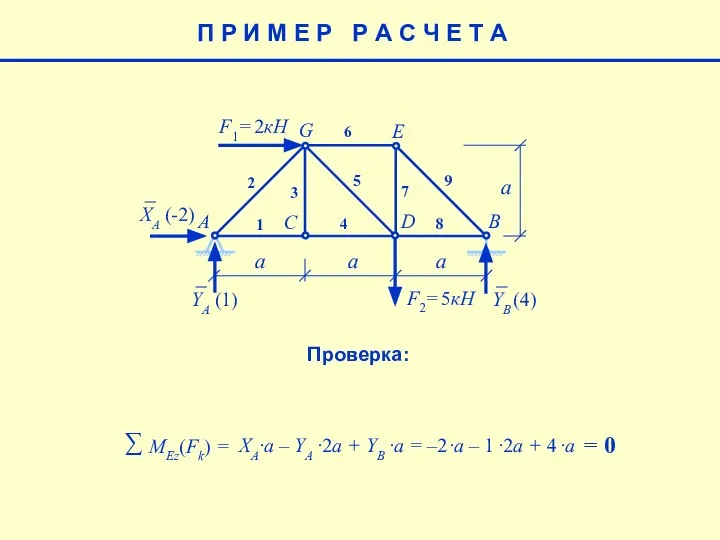
- 7. Проверка: Для проверки правильности полученных результатов составим уравнение моментов относительно такой точки, относительно которой все вычисленные
- 8. E a F1= 2кН F2= 5кН A B C D G 1 2 3 4 5
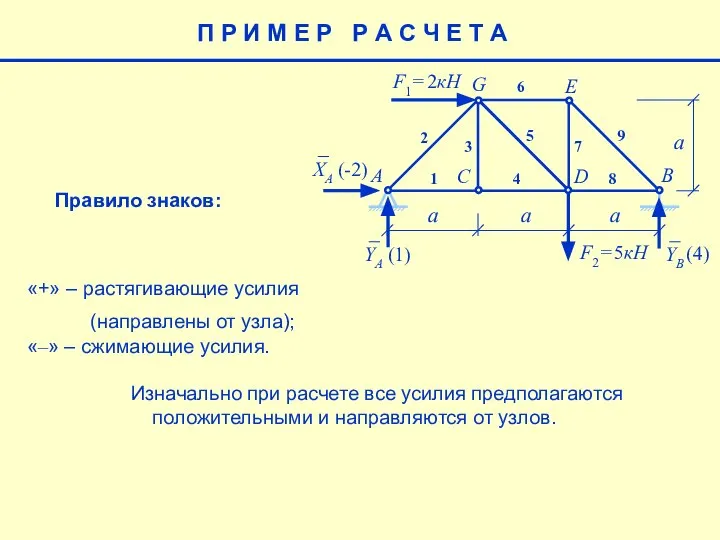
- 9. П Р И М Е Р Р А С Ч Е Т А
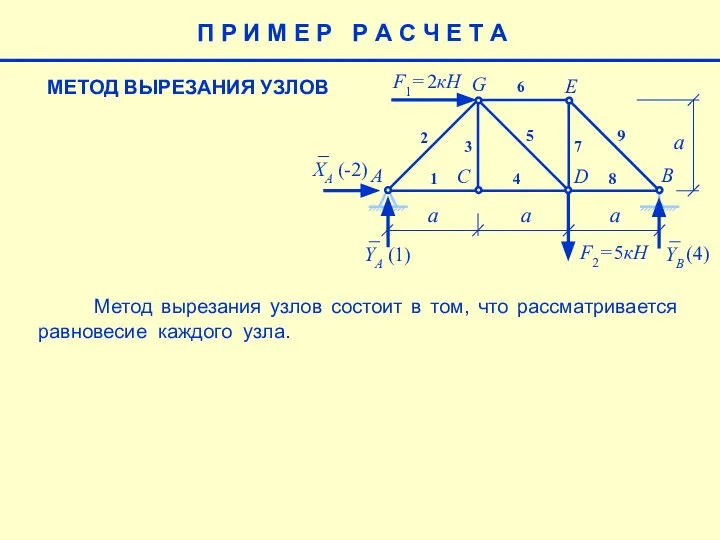
- 10. МЕТОД ВЫРЕЗАНИЯ УЗЛОВ П Р И М Е Р Р А С Ч Е Т А
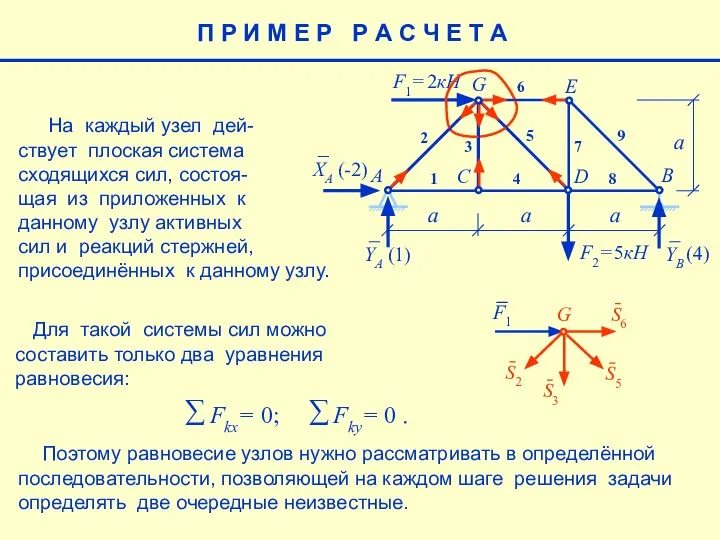
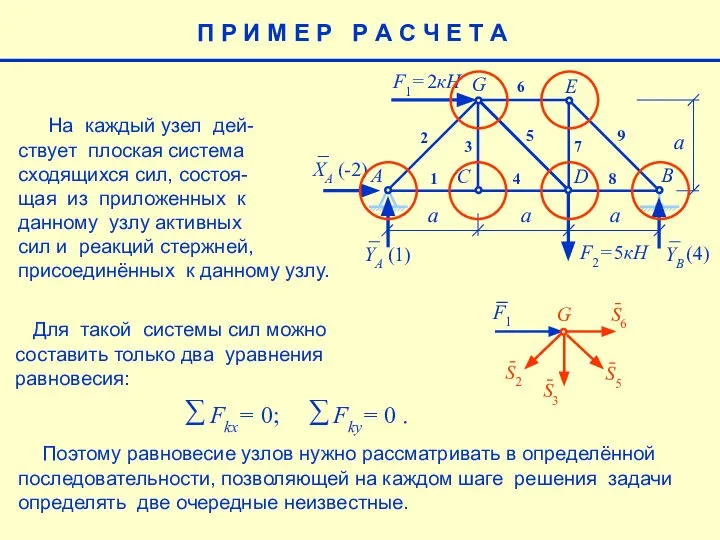
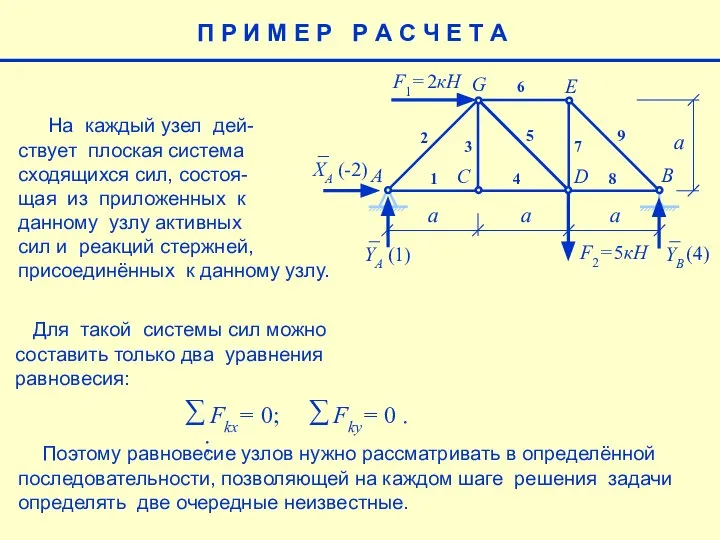
- 11. Поэтому равновесие узлов нужно рассматривать в определённой последовательности, позволяющей на каждом шаге решения задачи определять две
- 12. Поэтому равновесие узлов нужно рассматривать в определённой последовательности, позволяющей на каждом шаге решения задачи определять две
- 13. П Р И М Е Р Р А С Ч Е Т А На каждый узел
- 14. E a F1= 2кН F2= 5кН A B C D G 1 2 3 4 5
- 15. E a F1= 2кН F2= 5кН A B C D G 1 2 3 4 5
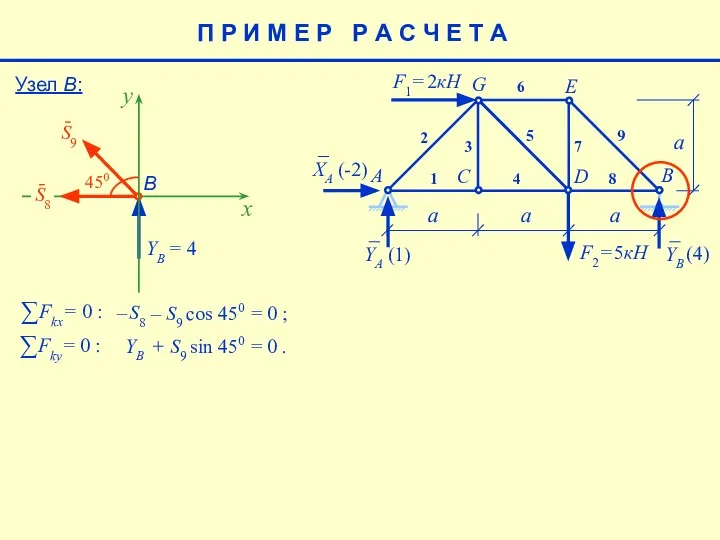
- 16. YB sin 450 – S9 cos 450 E a F1= 2кН F2= 5кН A B C
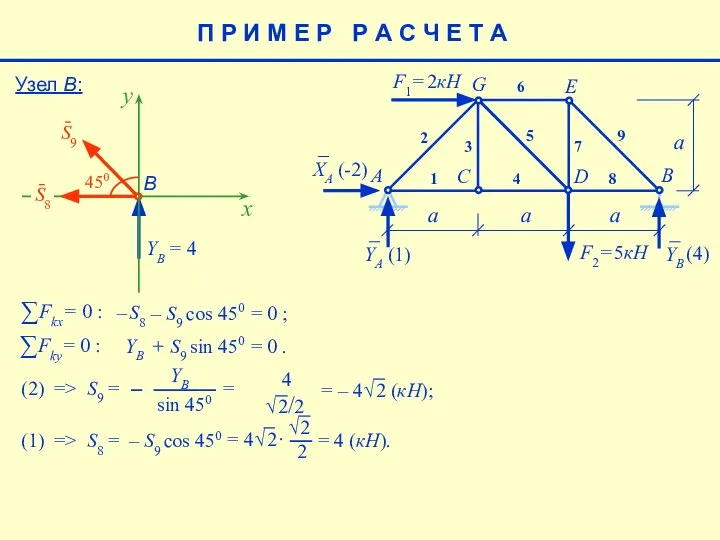
- 17. √ 2 2 E a F1= 2кН F2= 5кН A B C D G 1 2
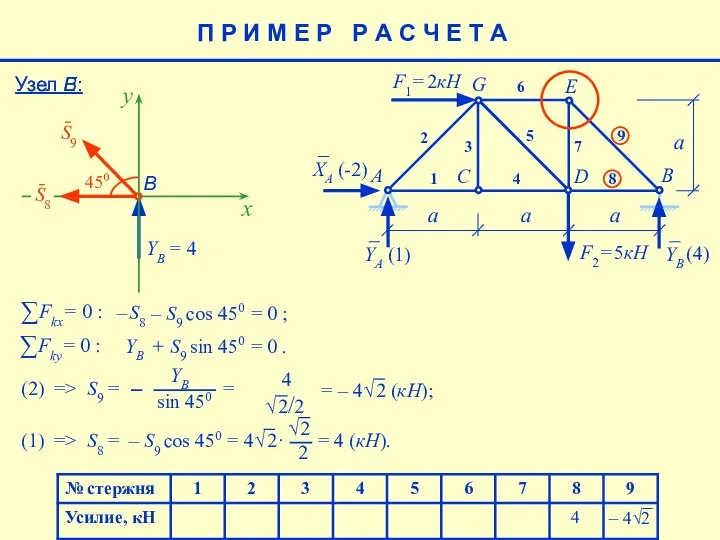
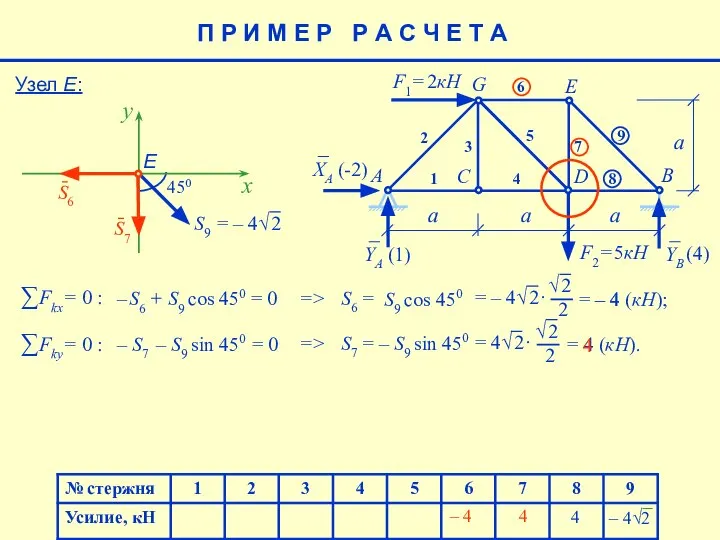
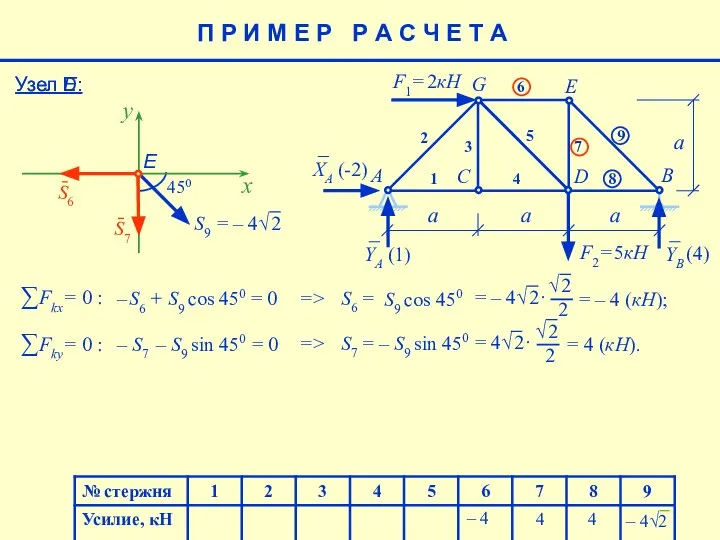
- 18. Узел Е: E a F1= 2кН F2= 5кН A B C D G 1 2 3
- 19. = – 4 (кН); Узел Е: 4 x – S6 + S9 cos 450 = 0
- 20. П Р И М Е Р Р А С Ч Е Т А 4 – 4
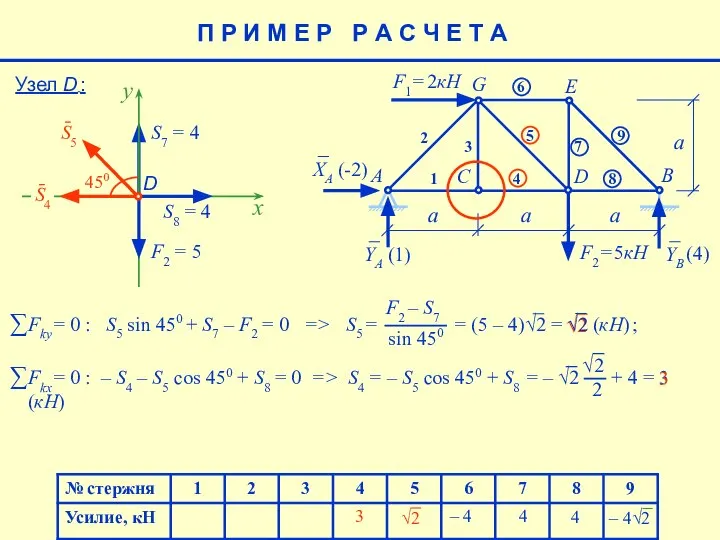
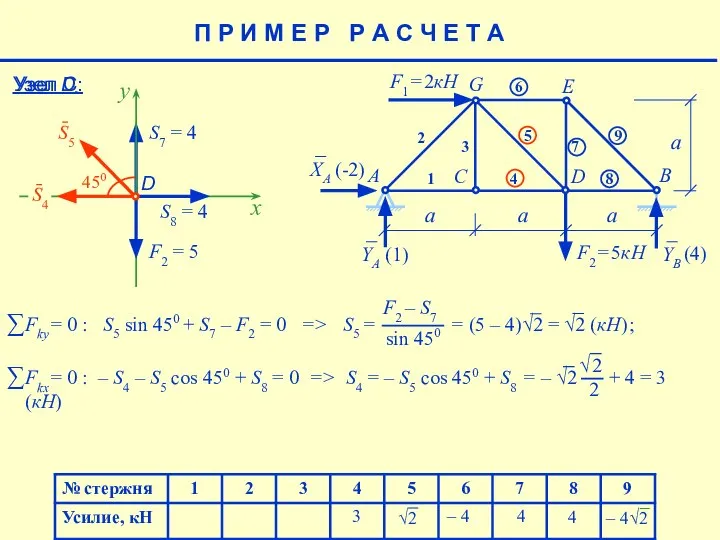
- 21. 4 – 4 4 (4) Узел D : S7 = 4 x S8 = 4 F2
- 22. 4 – 4 4 (4) √2 3 П Р И М Е Р Р А С
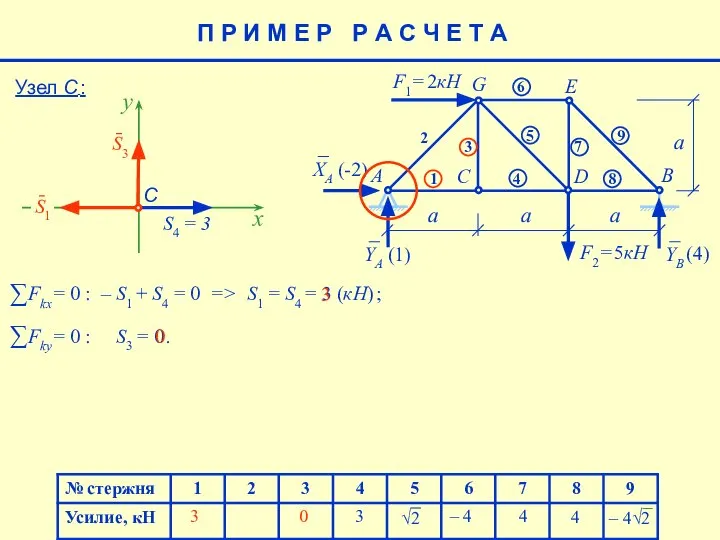
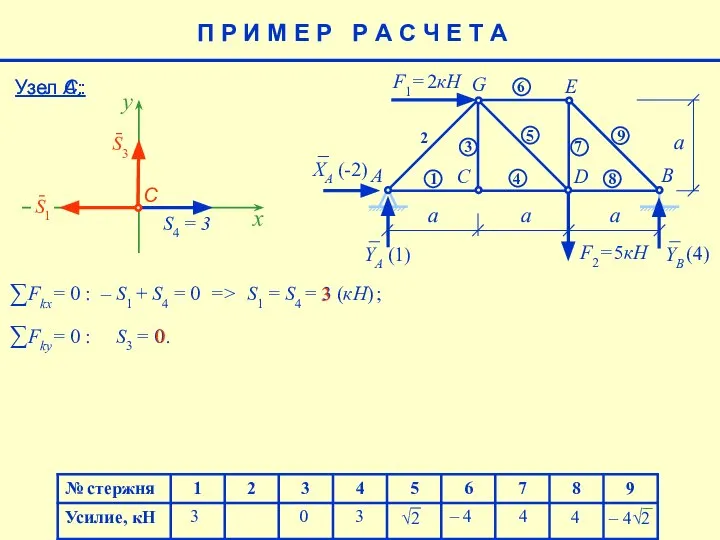
- 23. 4 – 4 4 (4) 3 Узел С : 3 0 3 0 П Р И
- 24. Узел А: 4 – 4 4 (4) 3 3 0 П Р И М Е Р
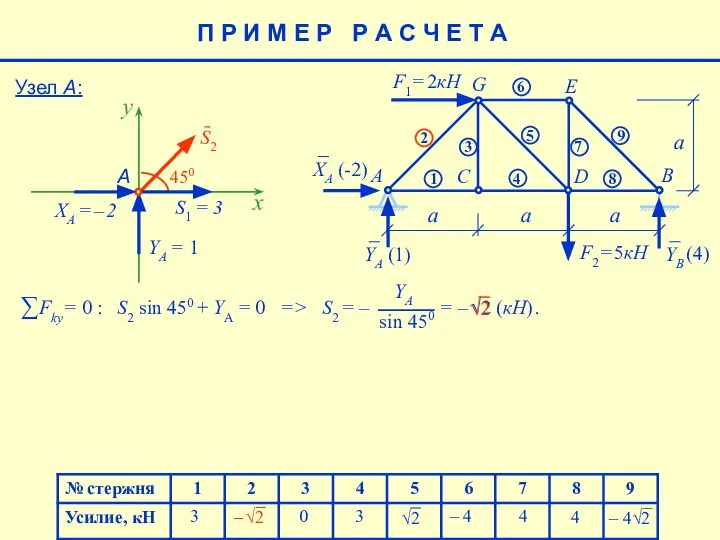
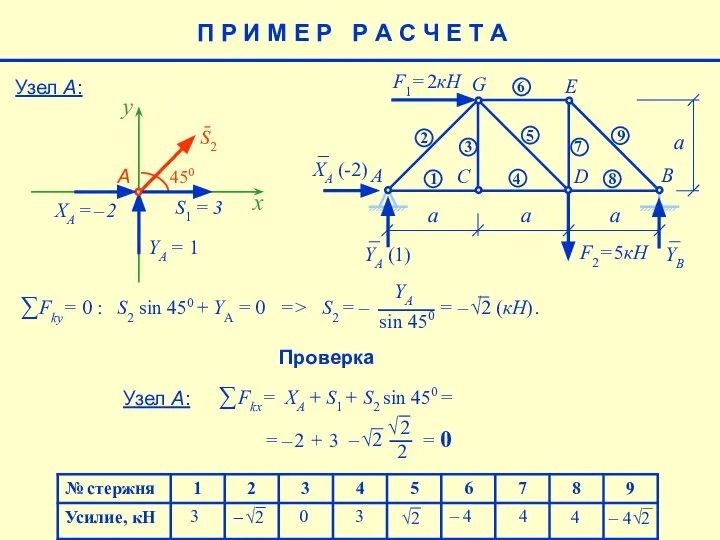
- 25. 4 – 4 4 (4) 3 3 0 Узел А: П Р И М Е Р
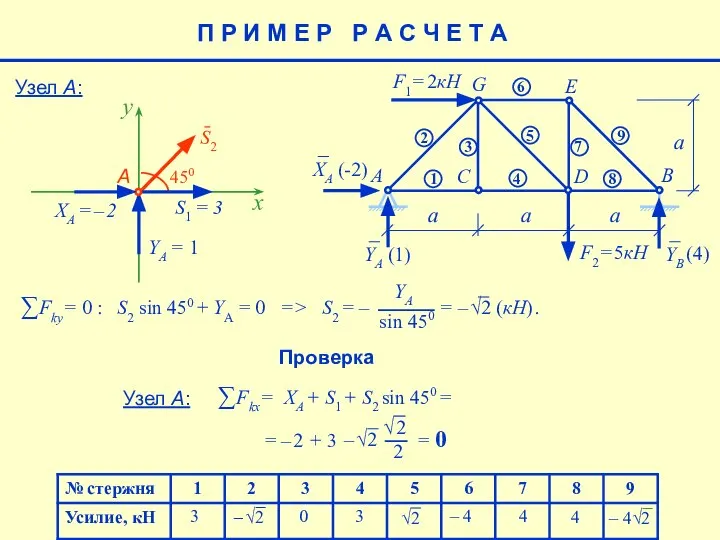
- 26. 4 – 4 4 (4) 3 3 0 Узел А: Проверка Узел А: XA + S1
- 27. 4 – 4 4 3 3 0 Проверка Узел А: П Р И М Е Р
- 29. Скачать презентацию

 Деление на 2, 3, 4, 5 (повторение)
Деление на 2, 3, 4, 5 (повторение) Дидактические материалы на уроках математики
Дидактические материалы на уроках математики Сумматор. Таблица истинности сумматора
Сумматор. Таблица истинности сумматора Деление на 4
Деление на 4 Определенный интеграл
Определенный интеграл Модели обслуживания вычислительных задач
Модели обслуживания вычислительных задач Сложение чисел с разными знаками
Сложение чисел с разными знаками Обратные тригонометрические функции
Обратные тригонометрические функции Стань умнее компьютера
Стань умнее компьютера Аксиомы стереометрии о взаимном расположении точек, прямых и плоскостей в пространстве
Аксиомы стереометрии о взаимном расположении точек, прямых и плоскостей в пространстве Письменное деление на двузначное число
Письменное деление на двузначное число Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності
Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Формулы половинного аргумента
Формулы половинного аргумента Умножение числа 4
Умножение числа 4 Площадь треугольника
Площадь треугольника Свойства степени
Свойства степени Треугольники вокруг нас
Треугольники вокруг нас Моделирование при управлении рисками авиапредприятий
Моделирование при управлении рисками авиапредприятий Основы дисперсионного анализа
Основы дисперсионного анализа Математика. Контрольная работа
Математика. Контрольная работа Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Математический диктант
Математический диктант Объёмные геометрические фигуры
Объёмные геометрические фигуры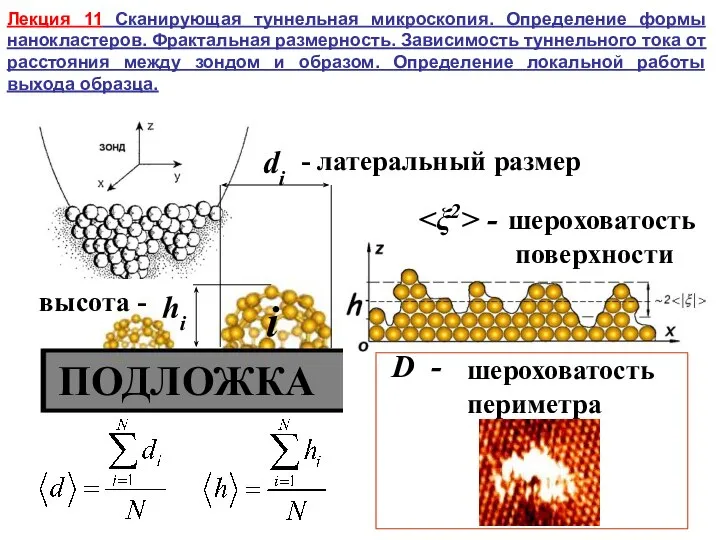 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Методы решения творческих задач
Методы решения творческих задач Особенности формирования понятия треугольник
Особенности формирования понятия треугольник Подготовка к ЕГЭ В-4. Курс лекций по математике
Подготовка к ЕГЭ В-4. Курс лекций по математике