Содержание
- 2. Вопрос 1. «Понятие множественной регрессии и корреляции»
- 3. Понятие модели множественной регрессии Модель множественной регрессии – это уравнение, отражающее корреляционную связь между результатом и
- 4. Цель множественной регрессии построить модель с несколькими факторами и определить при этом влияние каждого фактора в
- 5. Линейная функция множественной регрессии и корреляции Линейная функция множественной регрессии и корреляции имеет вид: у =
- 6. Нелинейная функция множественной регрессии и корреляции В качестве нелинейной функции множественной регрессии и корреляции чаще всего
- 7. Показательная функция Показательная функция имеет вид: у = а + b1x1 + b2x2 + bixi +
- 8. Степенная функция Степенная функция имеет вид: у = а + x1b1 + x2b2 + xibi +
- 9. Условия для проведения анализа методом множественной регрессии и корреляции 1. При проведении анализа методом множественной регрессии
- 10. Условия для проведения анализа методом множественной регрессии и корреляции 2. Результат и факторы – это количественные
- 11. Условия для проведения анализа методом множественной регрессии и корреляции 3. При построении эконометрической модели предполагается, что
- 12. Интеркорреляция и мультиколлинеарность Корреляционная связь, которая существует между двумя факторами, называется интеркорреляцией. Соответственно, корреляционная связь, существующая
- 13. Интеркорреляция и мультиколлинеарность Существование корреляционной связи между факторами выявляется с помощью коэффициентов корреляции, которые принято записывать
- 14. Интеркорреляция и мультиколлинеарность Наличие мультиколлинеарности подтверждается определителями матрицы. Если связь между факторами полностью отсутствует, то недиагональные
- 15. Вопрос 2. «Правила отбора факторов в модели множественной регрессии и корреляции»
- 16. Отбор факторов Несмотря на то, что теоретически множественная регрессионная модель позволяет учесть любое число факторов, практически
- 17. Отбор факторов Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых
- 18. Правила включения в модель факторов Включаемые в модель множественной регрессии факторы должны объяснять вариацию зависимой переменной.
- 19. Правила включения в модель факторов При включении в модель дополнительного фактора коэффициент (индекс) детерминации должен возрастать,
- 20. Правила включения в модель факторов Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии
- 21. Правила включения в модель факторов Множественная регрессия характеризуется наличием достаточно большого количества факторов. При этом отсутствует
- 22. Четыре метода подбора факторов при построении модели метод последовательного включения факторов метод исключения факторов из модели
- 23. Метод последовательного включения факторов При использовании метода последовательного включения факторов сначала должна быть построена модель с
- 24. Метод исключения факторов Использование метода исключения факторов предполагает, что сначала строится модель с максимально большим количеством
- 25. Шаговый регрессионный анализ Шаговый регрессионный анализ является преобразованием метода последовательного включения факторов. Построение модели начинается с
- 26. Ступенчатый регрессионный анализ Ступенчатый регрессионный анализ начинается с построения уравнения парной регрессии с наиболее значимым по
- 27. Фиктивные переменные и модель бинарного выбора Показатели, выбранные в качестве результативного признака и фактора, иногда могут
- 28. Модели с усеченными и цензурированными данными Чаще всего в моделях результативный признак является количественной переменной, однако
- 29. Модель с усеченными данными При усеченной выборке наблюдения производятся не над всей статистической совокупностью, а над
- 30. Модель с цензурированными данными Цензурированная выборка представляет собой данные наблюдения над всей статистической совокупностью, но в
- 31. Вопрос 3. «Показатели тесноты и силы связи между результативным признаком и факторами в уравнении множественной регрессии»
- 32. Коэффициенты (индексы) корреляции (детерминации) В парной линейной регрессии показатели тесноты связи называются коэффициентами корреляции (детерминации), в
- 33. Коэффициенты (индексы) корреляции Формулы для расчета коэффициентов (индексов) корреляции, при наличии двух факторов имеют вид:
- 34. Первая формула (первый фактор)
- 35. Вторая формула (второй фактор)
- 36. Третья формула (два фактора)
- 37. Совокупный коэффициент (индекс) множественной корреляции
- 38. Совокупный коэффициент (индекс) множественной корреляции
- 39. Интерпретация значений коэффициентов (индексов) корреляции 0,1- 0,3- слабая связь 0,3-0,5 – умеренная связь 0,5-0,7- заметная связь
- 40. Коэффициент (индекс) детерминации Коэффициент (индекс) детерминации определяется возведением в квадрат коэффициента (индекса) корреляции.
- 41. Коэффициент эластичности Ввиду того, что величины абсолютных показателей силы связи определяются единицами измерения факторов, они не
- 42. Коэффициент эластичности Коэффициенты эластичности показывают, на сколько процентов в среднем изменится результат при изменении фактора на
- 43. Коэффициент эластичности
- 44. Стандартизированные коэффициенты регрессии Во множественной регрессии и корреляции относительным показателем силы связи также являются стандартизированные коэффициенты
- 45. Вопрос 4. «Оценка параметров модели множественной регрессии и корреляции»
- 46. Несмещенность, эффективность и состоятельность оценок параметров Параметры уравнения множественной регрессии являются выборочными оценками неизвестных параметров по
- 47. Несмещенность, эффективность и состоятельность оценок параметров Оценка параметра является несмещенной, если ее математическое ожидание равно оцениваемому
- 48. Несмещенность, эффективность и состоятельность оценок параметров Оценка параметра является эффективной, если она имеет наименьшую дисперсию среди
- 49. Несмещенность, эффективность и состоятельность оценок параметров Оценка параметра является состоятельной, если с увеличением числа наблюдений оценка
- 50. Метод наименьших квадратов Наиболее простым методом оценки параметров уравнения множественной регрессии является метод наименьших квадратов Он
- 51. Метод максимального правдоподобия Если значения факторов и результативного признака не удовлетворяют перечисленным предпосылкам, то для нахождения
- 53. Скачать презентацию









































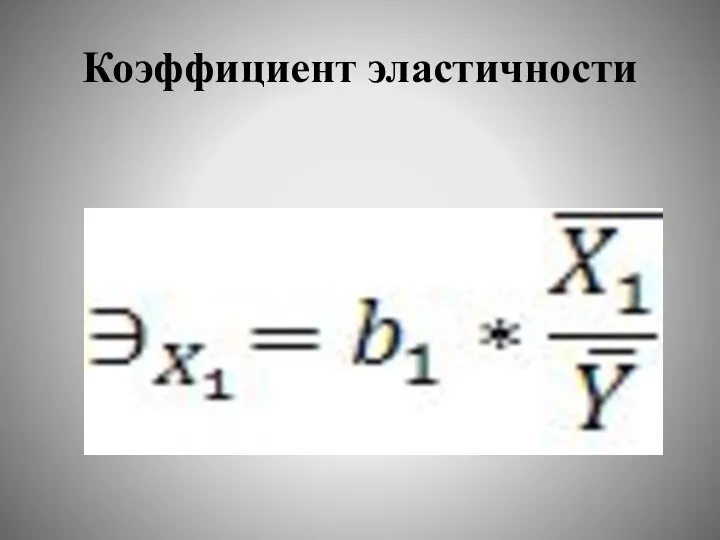








 Звёздчатые многогранники
Звёздчатые многогранники Число и цифра 6
Число и цифра 6 Обратная матрица
Обратная матрица Приёмы сложения однозначных чисел с переходом через десяток
Приёмы сложения однозначных чисел с переходом через десяток Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Презентация на тему Виды треугольников
Презентация на тему Виды треугольников  Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Прямое сложение и вычитание
Прямое сложение и вычитание Статистическая обработка массива однородных величин. Практическое занятие 2
Статистическая обработка массива однородных величин. Практическое занятие 2 Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Виды треугольников по углам
Виды треугольников по углам Эварист Галуа
Эварист Галуа Элементы комбинаторики
Элементы комбинаторики Проецирование на три взаимно перпендикулярные плоскости проекций
Проецирование на три взаимно перпендикулярные плоскости проекций Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ Математические методы в филологии
Математические методы в филологии Теоремы Менелая и Чевы
Теоремы Менелая и Чевы Кратные интегралы
Кратные интегралы Многогранники
Многогранники Одночлены. Обобщающий урок
Одночлены. Обобщающий урок Второй признак равенства треугольников. Геометрия , 7 класс
Второй признак равенства треугольников. Геометрия , 7 класс Задачи на части
Задачи на части Криволинейные интегралы
Криволинейные интегралы Математика 1 класс
Математика 1 класс Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Наибольшее и наименьшее значение функции на отрезке
Наибольшее и наименьшее значение функции на отрезке