Вписанная окружность

Касание прямой и окружности
касательная

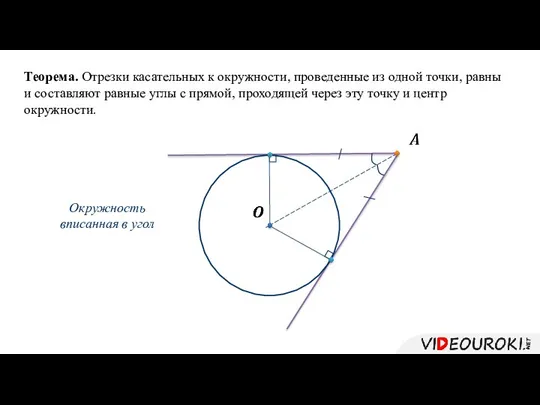
Теорема. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Окружность
вписанная в угол

Определение. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Описаны
около окружности
Не является описанным около окружности

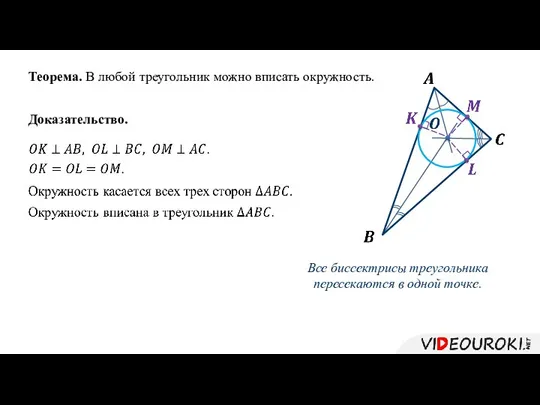
Теорема. В любой треугольник можно вписать окружность.
Доказательство.
Все биссектрисы треугольника пересекаются в одной точке.

Замечания.
1. В треугольник можно вписать только одну окружность.
Доказательство. Допустим, в треугольник можно вписать две окружности.
Тогда центр второй окружности был бы равноудален от всех сторон треугольника и лежал бы на пересечении его биссектрис.

Замечания.
2. В отличие от треугольника не во всякий четырехугольник можно вписать окружность.
Доказательство.
Рассмотрим прямоугольник, у которого смежные стороны не равны.
В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон, но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.е. нельзя вписать окружность.
Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
В любом описанном четырехугольнике суммы противоположных сторон равны.

Если в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
В любом описанном четырехугольнике суммы противоположных сторон равны.
Доказательство.
Отрезки касательных к окружности, проведенные из одной точки, равны.
Следовательно, суммы противоположных сторон в описанном четырехугольнике равны.

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Доказательство.

Можно ли описать около окружности ромб, квадрат и прямоугольник. Почему?

Решение.
Отрезки касательных к окружности, проведенные из одной точки, равны.