Слайд 2§ 1. Первообразная и неопределенный интеграл.
До сих пор мы рассматривали следующую задачу:

задана функция и требуется найти ее производную. Теперь будем рассматривать обратную задачу: будем находить функцию по заданной ее производной.
Слайд 3Интегрирование есть операция, обратная дифференцированию.
Определение 1. Функция F(x) называется первообразной функции f

(x) на промежутке X, если ∀ x ∈ X (F′(x) = f (x)).
Пример: y = x2.
F1(x) = x3/3
F1′(x) = (x3/3)′ = (1/3)(x3)′ = (1/3)3x2 = x2.
F2(x) = x3/3 + 1
F3(x) = x3/3 – 5,5
И вообще: F(x) = x3/3 + с, где с = const при любом с будет первообразной.
Слайд 4Первообразных у функции всегда бесконечное множество.
Имеем следующее: если F(x) является первообразной функции

f (x), то и любая функция вида F(x) + с тоже будет первообразной при любом с.
Возникает вопрос: а могут ли быть первообразные другого вида? Как показывает следующая теорема – нет.
Теорема (о первообразной). Пусть F(x) – первообразная функции f(x) на промежутке X, Ф(х) – какая-то другая функция. Ф(х) является первообразной f(x) на X тогда и только тогда, когда Ф(х) = F(x) + с, на Х, где с = const.
Слайд 5Доказательство
Необходимость. Пусть Ф(х) первообразная функции f(x) на X. Рассмотрим:
(Ф(х) - F(х))′ =

Ф′(х) - F′(х) = f(x) - f(x) = 0 ∀x∈X,
таким образом, этой функции ≡ 0 на Х. По критерию постоянства заключаем, что
Ф(х) - F(х) ≡ с на Х. Отсюда Ф(х) = F(x) + с на Х.
Достаточность. Пусть F(x) – первообразная функции f(x) и Ф(х) = F(x) + с, тогда
Ф′(х) = [F(x) + с]′ = F′(х) = f(x) и, стало быть, Ф(х) тоже производная на этом промежутке.
Ч.т.д.
Слайд 6Определение 2. Пусть F(х) первообразная функции f(x) на Х. Выражение вида F(x)

+ с, где с – произвольная постоянная (могущая принимать любые вещественные значения), называется неопределенным интегралом функции f(x) на данном промежутке.
Обозначается: ∫ f (x)dx = F(x) + с.
При этом f(x) называют подынтегральной функцией, а f(x)dx – подынтегральным выражением.
Таким образом, неопределенный интеграл есть семейство функций, а именно – множество всех первообразных функции f(x).
Слайд 7Таблица интегралов
∫0dx = c,
∫dx = x + c,
∫xμdx = + c, (μ

≠ -1)
= ln|x| + c,
∫axdx = + c,
∫exdx = ex + c,
∫sinxdx = -cosx + c,
∫cosxdx = sinx + c,
Слайд 8Продолжение таблицы интегралов
= tgx + c,
= - ctgx + c,

Слайд 9Чтобы доказать истинность каждой из этих формул, достаточно убедиться в том, что

производная правой части равна подынтегральной функции.
Докажем формулу 4.
= ln|x| + c.
Требуется доказать: (ln|x|)′ = .
а) Пусть x > 0. Тогда: (ln|x|)′ = (lnx)′ = .
b) Пусть x < 0. Тогда: (ln|x|)′ = (ln(-x))′ = .
Слайд 10Основные свойства неопределенного интеграла
Доказательство
Ч.т.д.
2) d ∫ f(x)dx = f(x)dx, (символы d и

∫ взаимно уничтожаются).
Доказательство
d ∫ f(x)dx = [∫ f(x)dx]′dx = f(x)dx.
Ч.т.д.
Слайд 11Основные свойства неопределенного интеграла (продолжение)
3) ∫df(x) = f(x) + c.
Интеграл от дифференциала

функции равен этой функции + с. Таким образом, символы ∫ и d взаимно уничтожаются.
Доказательство
∫df(x) = ∫f ′(x)dх = f(x) + c.
Ч.т.д.
Слайд 12Основные свойства неопределенного интеграла (продолжение)
4) ∫af(x)dx = ∫af(x)dx, (а ≠ 0) -

свойство однородности. Константу можно выносить за знак неопределенного интеграла.
Доказательство
Достаточно убедиться в том, что производная левой части равна производной правой части (в этом случае и в левой и в правой частях будет одно и тоже семейство первообразных).
[∫af(x)dx]′ = аf(x) (по первому свойству).
[a∫f(x)dx]′ = a [∫f(x)dx]′ = аf(x).
Ч.т.д.
Слайд 13Основные свойства неопределенного интеграла (продолжение)
5) Аддитивность относительно подынтеграль-ной функции.
∫[ f (x) ±

g(x)]dx = ∫ f (x)dx ± ∫g(x)dx.
Доказательство
Достаточно показать, что производная левой части равна производной правой части (в этом случае и в левой и в правой частях будет одно и тоже семейство первообразных).
{∫[ f (x) ± g(x)]}′ = f (x) ± g(x).
[∫ f (x)dx ± ∫g(x)dx]′ = [∫f(x)dx]′ ± [∫g(x)dx]′ =
= f (x) ± g(x).
Ч.т.д.
Слайд 14Замечание 1. Свойство аддитивности справед-ливо для любого конечного числа слагаемых.
Замечание 2. Вычисление

интегралов называ-ется интегрированием.
Слайд 15§ 2. Интегрирование с помощью замены переменных (метод подстановки).
Сущность метода заключается в

следующем:
∫ f (x)dх с помощью подстановки x = ϕ(t)
приводят к другому, более простому для вычисления, то есть подбирают функцию
x = ϕ(t) так, чтобы
∫ f (ϕ(t))dϕ(t) = ∫ f (ϕ(t))ϕ′(t)dt
был более простым для вычисления.
Слайд 16Теорема (о подстановке). Пусть ∫ f (t)dt =F(t)+c, при этом t =

ϕ(х), тогда:
∫ f (ϕ(х))dϕ(х) = F(ϕ(х)) + c,
или
f (ϕ(х))ϕ′(х)dх = F(ϕ(х)) + c,
функции f, ϕ, ϕ′ считаем непрерывными.
Доказательство
Достаточно проверить, что:
[F(ϕ(х))]′ = f (ϕ(х))ϕ′(х)
Действительно,
Fx′ = Ft′tx′ =* f (t)ϕ′(t) = f (ϕ(х))ϕ′(х).
* справедливо так как по условию F(ϕ) первообразная для f (х). Ч.т.д.
Слайд 17Пример 1.
∫sin3xcosxdх =(*)= ∫sin3xdsinx = [sinx = t] = ∫t3dt =
=
![Пример 1. ∫sin3xcosxdх =(*)= ∫sin3xdsinx = [sinx = t] = ∫t3dt =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1132499/slide-16.jpg)
t4/4 + с = (1/4)sin4x + с.
Замечание 3. На шаге (*) мы осуществили так называемое внесение функции под знак дифференциала.
Пример 2.
= ∫lnxdlnx = [lnx = t] = ∫tdt =
= t2/2 + с = (1/2)ln2x + с.
Слайд 18Из теоремы о подстановке можно извлечь один очень важный вывод, а именно,

можно написать, что:
∫ f (t)dt⎪t = ϕ(x) = ∫ f (ϕ(x))ϕ′(x)dx
Для удобства поменяем x и t местами:
∫ f (x)dx⎪x = ϕ(t) = ∫ f (ϕ(t))ϕ′(t)dt
Будем предполагать, что существует обратная функция x = ϕ(t) → t = ϕ-1(x).
Таким образом, получим следующее:
∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt⎪t = ϕ-1(x)
Слайд 19Отсюда получаем правило для вычисления интеграла методом подстановки: чтобы вычислить ∫ f

(x)dx с помощью подстановки
x = ϕ(t) нужно под знаком интеграла вместо x везде подставить ϕ(t) (в подынтегральной функции, а также вместо dx мы подставляем ϕ′(t)dt).
Вычисляем полученный интеграл, зависящий от t. Ответ получаем в терминах переменной t. Чтобы получить окончательный результат, нужно перейти к прежней переменной x исходя из самой подстановки.
Слайд 20Замечание 4. Внесение под знак дифференциала есть частный случай метода подстановки.
Метод подстановки

– один из самых сильных методов интегрирования.
Пример 3.
∫(2х + 3)10dх = = (1/2)∫t10dt =
= (1/2)t11/11 + с = (1/22) (2х + 3)11 + с.















![Пример 1. ∫sin3xcosxdх =(*)= ∫sin3xdsinx = [sinx = t] = ∫t3dt =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1132499/slide-16.jpg)




 Куб
Куб Площадь и объём фигуры
Площадь и объём фигуры Логарифмическая спираль
Логарифмическая спираль Проценты и десятичные дроби
Проценты и десятичные дроби Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Правила вычисления производных
Правила вычисления производных Презентация на тему Арифметика Магницкого
Презентация на тему Арифметика Магницкого  Презентация на тему Площади многоугольников
Презентация на тему Площади многоугольников  Построение конуса с вырезом
Построение конуса с вырезом Функция. Предел функции. (часть 1)
Функция. Предел функции. (часть 1) Презентация на тему Формирование УУД на уроках математики в 5 классе
Презентация на тему Формирование УУД на уроках математики в 5 классе  Упрощение выражений (5 лкасс)
Упрощение выражений (5 лкасс) Решение логических задач
Решение логических задач Уравнения и неравенства с параметрами. 11 класс
Уравнения и неравенства с параметрами. 11 класс Функция. Свойства функций. Урок №1
Функция. Свойства функций. Урок №1 Десятки. Мозаика заданий
Десятки. Мозаика заданий Многогранник
Многогранник Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах
Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах Различные способы доказательств в курсе геометрии
Различные способы доказательств в курсе геометрии Две задачи на дроби
Две задачи на дроби Треугольник
Треугольник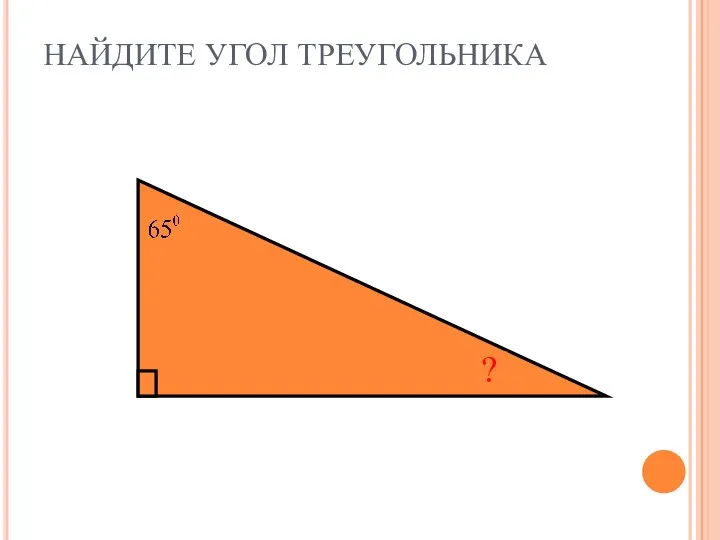 Нахождение угла треугольника
Нахождение угла треугольника Презентация на тему Тригонометрия
Презентация на тему Тригонометрия  Презентация на тему Умножение десятичных дробей (5 класс)
Презентация на тему Умножение десятичных дробей (5 класс)  Взаимное расположение графиков линейных функций. 7 класс
Взаимное расположение графиков линейных функций. 7 класс Парная линейная регрессия
Парная линейная регрессия Презентация на тему ШАРАДЫ, МЕТАГРАММЫ, ЛОГОГРИФЫ
Презентация на тему ШАРАДЫ, МЕТАГРАММЫ, ЛОГОГРИФЫ