Prezentatsia_2

*
Математические модели
Основным языком информационного моделирования в науке является язык математики.
Модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Математическая модель - информационная модель, в которой параметры и зависимости между ними выражены в математической форме.

*
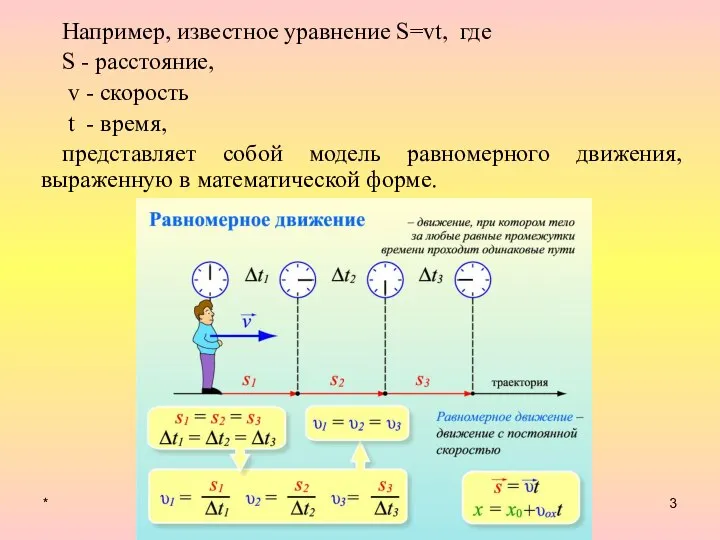
Например, известное уравнение S=vt, где
S - расстояние,
v - скорость
t - время,
представляет собой модель равномерного движения, выраженную в математической форме.

*
Рассматривая физическую систему: тело массой m, скатывающееся по наклонной плоскости с ускорением a под воздействием силы F, Ньютон получил соотношение F = mа.
Это математическая модель физической системы.

*
Метод моделирования дает возможность применять математический аппарат к решению практических задач. Понятия числа, геометрической фигуры, уравнения, являются примерами математических моделей.
К методу математического моделирования в учебном процессе приходится прибегать при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее необходимо вначале перевести на язык математики (построить математическую модель).
Математическое моделирование

*
При математическом моделировании исследование объекта осуществляется посредством изучения модели, сформулированной на языке математики.
Пример: нужно определить площадь поверхности стола. Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью прямоугольником. Площадь этого прямоугольника и считается искомой.
Из всех свойств стола выделили три: форма поверхности (прямоугольник) и длины двух сторон. Не важны ни цвет стола, ни материал, из которого он сделан, ни то, как он используется.
Предположив, что поверхность стола – прямоугольник, легко указать исходные данные и результат. Они связаны соотношением S=ab.

*
Рассмотрим пример приведения решения конкретной задачи к математической модели.
Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Даны некоторые предположения о формах сундука и окнах иллюминатора и исходные данные решения задачи.
Предположения:
Иллюминатор имеет форму круга. Сундук имеет форму прямоугольного параллелепипеда.
Исходные данные: D - диаметр иллюминатора; x - длина сундука; y - ширина сундука; z - высота сундука.
Конечный результат: Сообщение: можно или нельзя вытащить.

*
Если , то сундук можно вытащить, а если
, то нельзя.
Системный анализ условия задачи выявил связи между размером иллюминатора и размерами сундука, учитывая их формы. Полученная в результате анализа информация отобразилась в формулах и соотношениях между ними, так возникла математическая модель.
Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом:

*
Пример 1:
Вычислить количество краски для покрытия пола в спортивном зале.
Для решения задачи нужно знать площадь пола. Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок.
Пусть A – длина пола, B - ширина пола, S1 - площадь, которую можно покрыть содержимым одной банки, N – количество банок.
Площадь пола вычисляем по формуле S=A×B, а количество банок, необходимых для покраски зала, N= A×B/S1.

*
Пример 2:
Через первую трубу бассейн наполняется за 30 часов, через вторую трубу – за 20 часов. За сколько часов бассейн наполнится через две трубы?
Решение:
Обозначим время заполнения бассейна через первую и вторую трубу А и В соответственно. Примем за 1 весь объём бассейна, искомое время обозначим через t.
Так как через первую трубу бассейн наполняется за А часов, то 1/А –часть бассейна, наполняемая первой трубой за 1 час; 1/В - часть бассейна, наполняемая второй трубой за 1 час.
Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1/А+1/В.
Можно записать: (1/А+1/В)t=1. получили математическую модель, описывающую процесс наполнения бассейна из двух труб.
Искомое время можно вычислить по формуле:

*
Пример 3:
На шоссе расположены пункты А и В, удалённые друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном А со скоростью 50 км/ч.
Составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов.
За t часов мотоциклист проедет 50t км и будет находится от А на расстоянии 50t км + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой: S=50t + 20, где t>0.

*
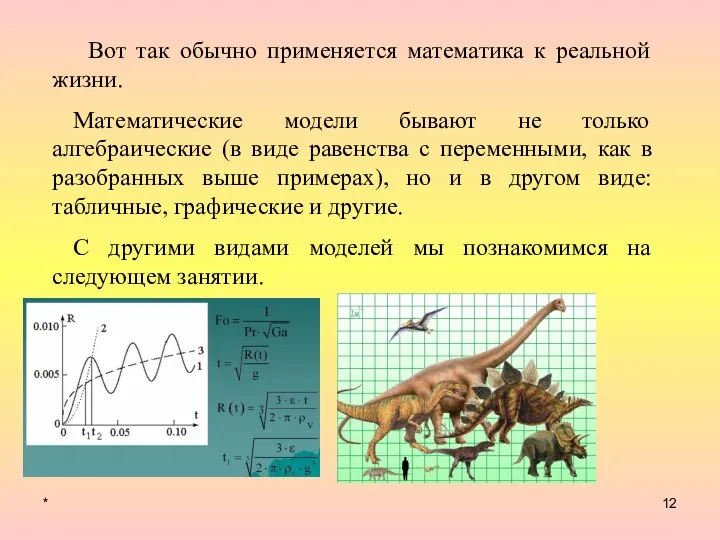
Вот так обычно применяется математика к реальной жизни.
Математические модели бывают не только алгебраические (в виде равенства с переменными, как в разобранных выше примерах), но и в другом виде: табличные, графические и другие.
С другими видами моделей мы познакомимся на следующем занятии.