Содержание
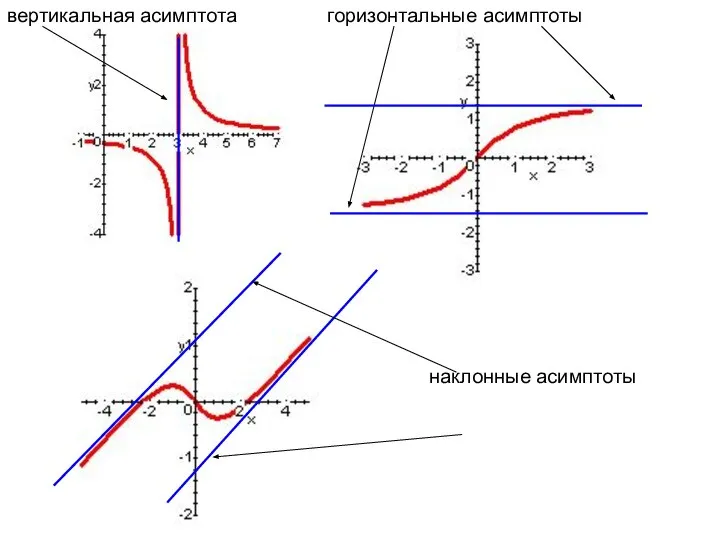
- 2. вертикальная асимптота горизонтальные асимптоты наклонные асимптоты
- 3. Асимптоты графика функции. Теорема 1. Если то прямая x=a является вертикальной асимптотой графика функции y=f(x).
- 4. Асимптоты графика функции. Cледствие. Вертикальные асимптоты следует искать в точках разрыва области определения и на концах
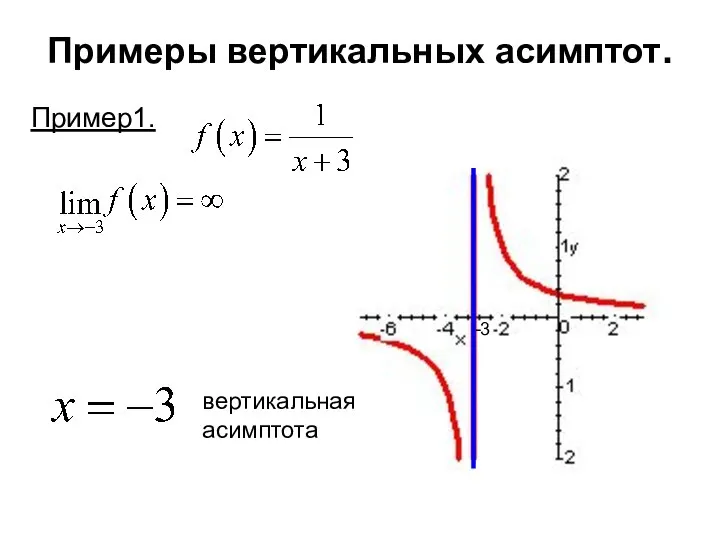
- 5. Примеры вертикальных асимптот. Пример1.
- 6. Примеры вертикальных асимптот. Пример1. -3 вертикальная асимптота
- 7. Примеры вертикальных асимптот. Пример 2.
- 8. Асимптоты графика функции. Теорема 2. Если , то прямая y=a является горизонтальной асимптотой.
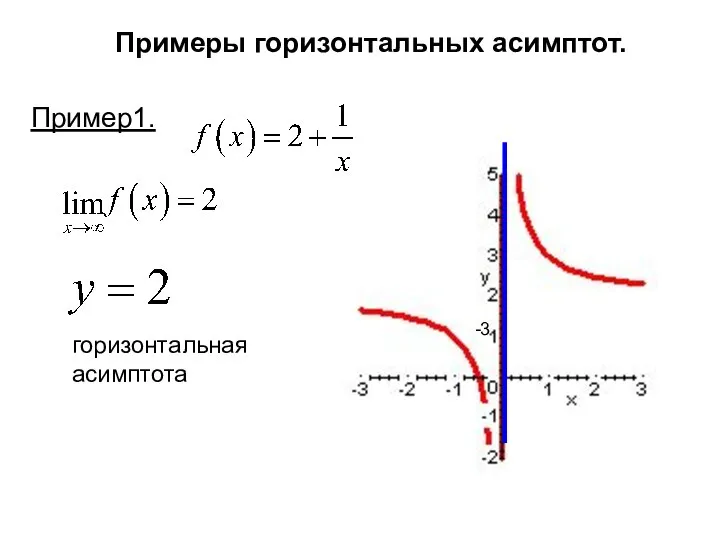
- 9. Примеры горизонтальных асимптот. Пример1.
- 10. Примеры горизонтальных асимптот. Пример1. -3 горизонтальная асимптота
- 11. Теорема 3. Если , то прямая y=ax+b является наклонной асимпто- той. Асимптоты графика функции.
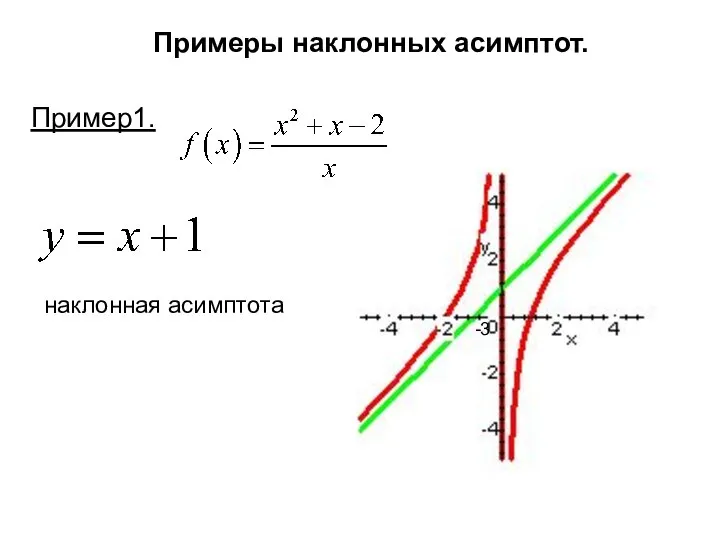
- 12. Примеры наклонных асимптот. Пример1.
- 13. Примеры наклонных асимптот. Пример1.
- 14. Примеры наклонных асимптот. Пример1. -3 наклонная асимптота
- 15. Замечание. Горизонтальная асимптота является частным случаем наклонной асимптоты y=ax+b Если а=0, то наклонная асимптота становится горизонтальной.
- 16. Общая схема исследования функций. Область определения. Исследование на четность-нечетность. Асимптоты. Экстремумы и интервалы монотонности. Точки перегиба
- 17. Пример 1. Область определения
- 18. Пример 1. Область определения
- 19. Пример 2. Исследование на четность-нечетность. f(-x)=……
- 20. Пример 2. Исследование на четность-нечетность. Функция общего вида
- 21. Пример 3. Асимптоты А) вертикальные x=3 – точка разрыва
- 22. Пример 3. Асимптоты А) вертикальные x=3 – точка разрыва x=3 – вертикальная асимптота
- 23. Пример 3. Асимптоты б) горизонтальные и наклонные y=ax+b
- 24. Пример 3. Асимптоты в) наклонные y=ax+b
- 25. Пример 3. Асимптоты в) наклонные y=ax+b
- 26. Пример 3. Асимптоты в) наклонные y=ax+b y=x-3 – наклонная асимптота, горизонтальных асимптот нет
- 27. Пример 4. Экстремумы и интервалы монотонности
- 28. Пример 4. Экстремумы и интервалы монотонности
- 29. Пример 4. Экстремумы и интервалы монотонности
- 30. Пример 4. Экстремумы и интервалы монотонности 1 3 5 + + - - т. max т.
- 31. Пример 4. Экстремумы и интервалы монотонности 1 3 5 + + - - т. max т.
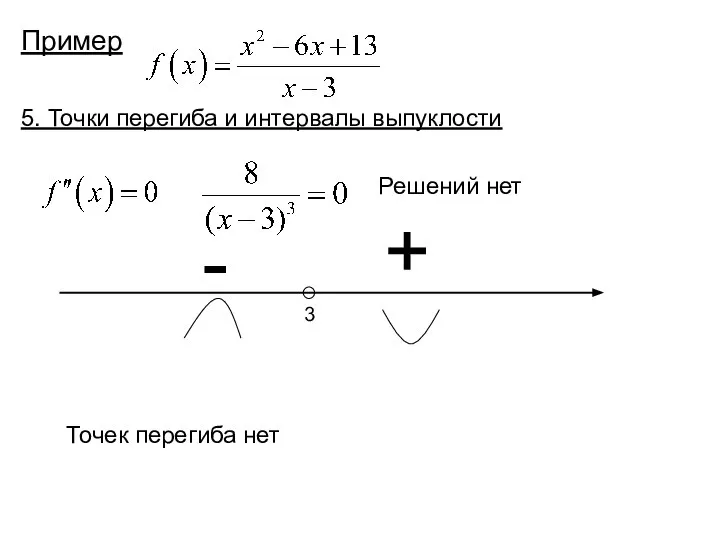
- 32. Пример 5. Точки перегиба и интервалы выпуклости
- 33. Пример 5. Точки перегиба и интервалы выпуклости
- 34. Пример 5. Точки перегиба и интервалы выпуклости 3 + - Решений нет Точек перегиба нет
- 35. Пример 6. Точки пересечения с осями координат. С осью OX y=0
- 36. Пример 6. Точки пересечения с осями координат. С осью OX y=0 Точек пересечения с OX нет
- 37. Пример 6. Точки пересечения с осями координат. С осью OY x=0
- 38. Пример 6. Точки пересечения с осями координат. С осью OY x=0
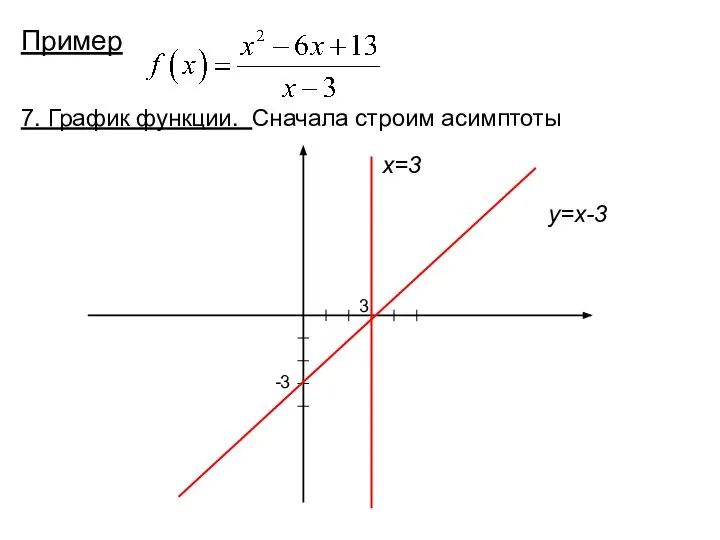
- 39. Пример 7. График функции. Сначала строим асимптоты 3 -3 x=3 y=x-3
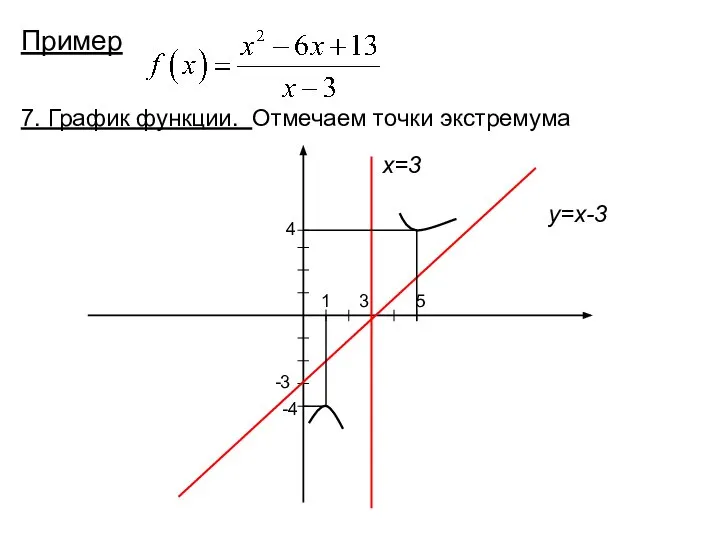
- 40. Пример 7. График функции. Отмечаем точки экстремума 3 -3 x=3 y=x-3 5 1 -4 4
- 42. Скачать презентацию
































 Мысли о ЕГЭ
Мысли о ЕГЭ Высота треугольника
Высота треугольника Роль геометрии в изобразительном искусстве
Роль геометрии в изобразительном искусстве Представление информации. Решение задач на проценты
Представление информации. Решение задач на проценты Влияние математических действий на аликвоты
Влияние математических действий на аликвоты Экстремумы функции (пример)
Экстремумы функции (пример) Параллельность плоскостей
Параллельность плоскостей Математическое описание случайных явлений
Математическое описание случайных явлений Операции над графами
Операции над графами Консультация ДУ
Консультация ДУ Квадратные уравнения
Квадратные уравнения Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Геометрическое место точек. 7 класс
Геометрическое место точек. 7 класс Сантиметр. Линейка
Сантиметр. Линейка Решение задач
Решение задач Вычисление производной
Вычисление производной Сколько раз в день минутная и часовая стрелки образуют прямую линию?
Сколько раз в день минутная и часовая стрелки образуют прямую линию? Сплайн интерполяция. Отчёт по домашней работе №3
Сплайн интерполяция. Отчёт по домашней работе №3 Решение иррациональных уравнений
Решение иррациональных уравнений Презентация по математике "Перестановка слагаемых" -
Презентация по математике "Перестановка слагаемых" -  Критерий Пирсона
Критерий Пирсона К В Н 8 – 9 классы «И прекрасна, и сильна Математика – страна»
К В Н 8 – 9 классы «И прекрасна, и сильна Математика – страна» Понятие функции. Свойства функций
Понятие функции. Свойства функций Неопределённый интеграл
Неопределённый интеграл Графический метод решения систем уравнений
Графический метод решения систем уравнений Построение графика функции с помощью производной
Построение графика функции с помощью производной Использование прикладных программ для оптимизации задач исследования. Контрольная работа
Использование прикладных программ для оптимизации задач исследования. Контрольная работа