Содержание
- 2. Прямая у = 4х + 11 параллельна касательной к графику функции у = х2 + 8х
- 3. Прямая у = 3х + 11 является касательной к графику функции у = x3 − 3x2
- 4. На рисунке изображен график у = f ′(x) – производной функции f(x), определенной на интервале (–10;
- 5. На рисунке изображен график у = f ′(x) – производной функции f(x), определенной на интервале (–8;
- 6. Решение: Заметим, что на интервале (–4; 8) производная в точке хо = 4 обращается в 0
- 7. №6 На рисунке изображен график у = f ′(x) – производной функции f(x), определенной на интервале
- 8. №7 На рисунке изображен график функции у = f(x), определенной на интервале (–6; 5). Определите количество
- 9. 0 у = f(x) –6 6 у х 2 4 6 3 5 1 №8 На
- 10. №9 На рисунке изображен график у = f(x) – производной функции f(x), определенной на интервале (–7;
- 11. 180°− α №10 На рисунке изображен график функции у = f(x), определенной на интервале (–10; 2)
- 12. . На рисунке изображен график производной у = f ′(x) –функции f(x), определенной на интервале (–11;
- 13. Прямая у = 4х – 4 является касательной к графику функции ах2 + 34х + 11.
- 14. Прямая у = – 4х – 5 является касательной к графику функции 9х2 + bх +
- 15. Прямая у = 2х – 6 является касательной к графику функции х2 + 12х + с.
- 16. Материальная точка движется прямолинейно по закону x(t) = 0,5t2 – 2t – 6, где x –
- 17. Материальная точка движется прямолинейно по закону x(t) = 0,5t2 – 2t – 22, где x –
- 18. На рисунке изображен график функции у = f(x), определенной на интервале (–8; 6). Найдите сумму точек
- 19. На рисунке изображен график производной у = f ′(x) – функции f(x), определенной на интервале (–10;
- 21. Скачать презентацию
Слайд 2Прямая у = 4х + 11 параллельна касательной к графику функции у
Прямая у = 4х + 11 параллельна касательной к графику функции у

Найдите абсциссу точки касания.
Решение:
Если прямая параллельна касательной к графику функции в какой-то точке (назовем ее хо), то ее угловой коэффициент (в нашем случае k = 4 из уравнения у = 4х +11) равен значению производной функции в точке хо:
k = f ′(xo) = 4
Производная функции
f ′(x) = (х2 + 8х + 6)′ = 2x + 8.
Значит, для нахождения искомой точки касания необходимо, чтобы 2хo + 8 = 4,
откуда хо = – 2.
Ответ: – 2.
№1
Слайд 3Прямая у = 3х + 11 является касательной к графику
функции у
Прямая у = 3х + 11 является касательной к графику
функции у

Найдите абсциссу точки касания.
Решение:
Заметим, что если прямая является касательной к графику, то ее угловой коэффициент (k = 3) должен быть равен производной функции в точке касания, откуда имеем Зх2 − 6х − 6 = 3, то есть Зх2 − 6х − 9 = 0 или х2 − 2х − 3 = 0. Это квадратное уравнение имеет два корня: −1 и 3. Таким образом есть две точки, в которых касательная к графику функции у = х3 − Зх2 − 6х + 6 имеет угловой коэффициент, равный 3.
Для того чтобы определить, в какой из этих двух точек прямая
у = 3х + 11 касается графика функции, вычислим значения функции в этих точках и проверим, удовлетворяют ли они уравнению касательной.
Значение функции в точке −1 равно у(−1) = −1 − 3 + 6 + 6 = 8,
а значение в точке 3 равно у(3) = 27 − 27 − 18 + 6 = −12. Заметим, что точка с координатами (−1; 8) удовлетворяет уравнению касательной, так как 8 = −3 + 11. А вот точка (3; −12) уравнению касательной не удовлетворяет, так как −12 ≠ 9 + 11.
Значит, искомая абсцисса точки касания равна −1.
Ответ: −1.
№2
Слайд 4На рисунке изображен график у = f ′(x) – производной функции f(x),
На рисунке изображен график у = f ′(x) – производной функции f(x),
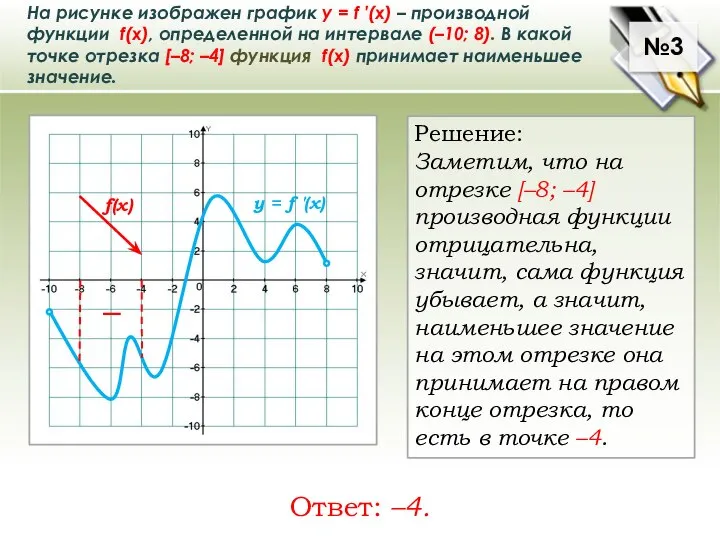
Решение:
Заметим, что на отрезке [–8; –4]
производная функции
отрицательна, значит, сама функция убывает, а значит,
наименьшее значение на этом отрезке она принимает на правом
конце отрезка, то есть в точке –4.
Ответ: –4.
№3
–
у = f ′(x)
f(x)
Слайд 5На рисунке изображен график у = f ′(x) – производной функции f(x), определенной
На рисунке изображен график у = f ′(x) – производной функции f(x), определенной
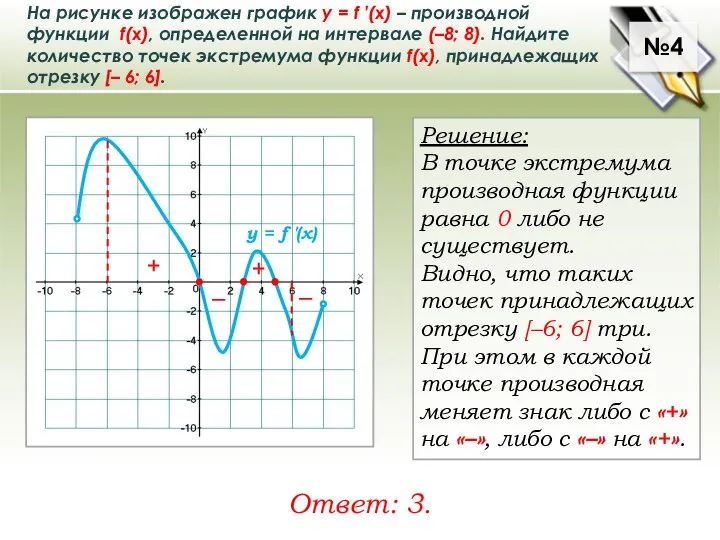
Решение:
В точке экстремума производная функции
равна 0 либо не существует.
Видно, что таких точек принадлежащих отрезку [–6; 6] три. При этом в каждой точке производная меняет знак либо с «+» на «–», либо с «–» на «+».
Ответ: 3.
№4
+
–
–
+
у = f ′(x)
Слайд 6Решение:
Заметим, что на интервале (–4; 8) производная в точке
хо =
Решение:
Заметим, что на интервале (–4; 8) производная в точке
хо =
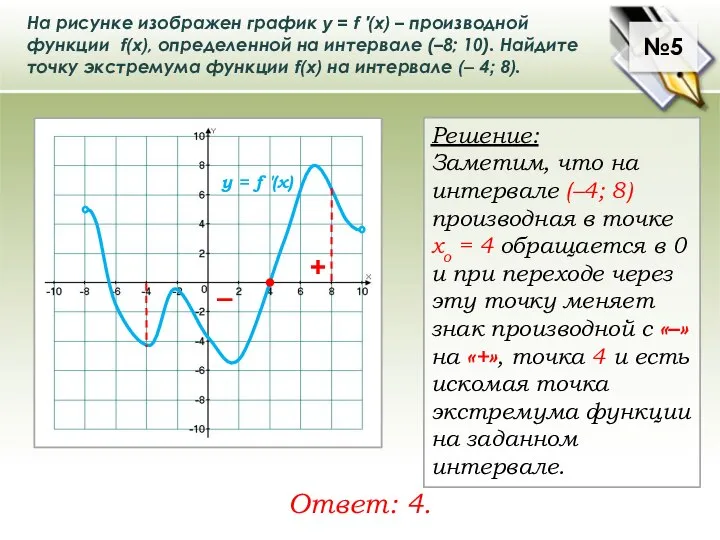
№5
На рисунке изображен график у = f ′(x) – производной функции f(x), определенной на интервале (–8; 10). Найдите точку экстремума функции f(x) на интервале (– 4; 8).
.
Ответ: 4.
–
+
у = f ′(x)
Слайд 7№6
На рисунке изображен график у = f ′(x) – производной функции f(x), определенной
№6
На рисунке изображен график у = f ′(x) – производной функции f(x), определенной
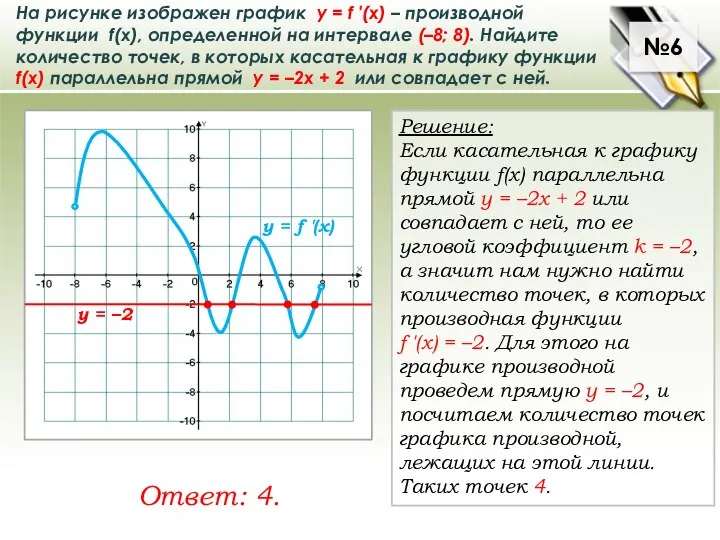
Ответ: 4.
Решение:
Если касательная к графику функции f(x) параллельна прямой у = –2x + 2 или совпадает с ней, то ее угловой коэффициент k = –2, а значит нам нужно найти
количество точек, в которых производная функции
f ′(x) = –2. Для этого на графике производной проведем прямую у = –2, и посчитаем количество точек графика производной, лежащих на этой линии. Таких точек 4.
у = f ′(x)
у = –2
Слайд 8№7
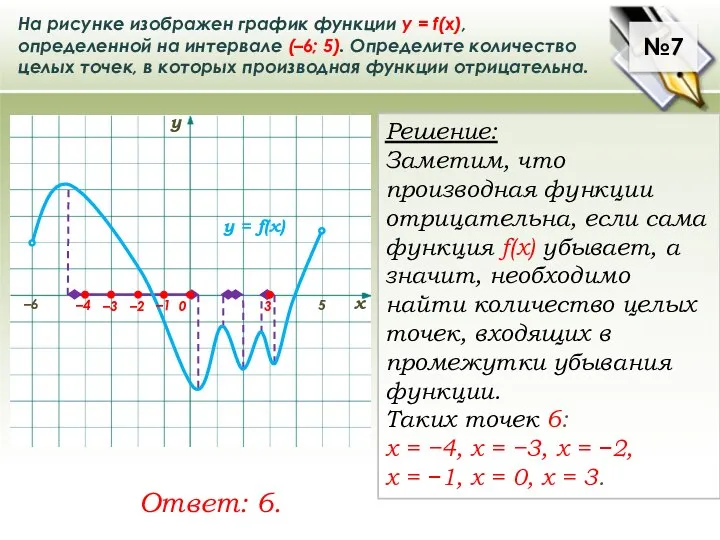
На рисунке изображен график функции у = f(x), определенной на интервале (–6;
№7
На рисунке изображен график функции у = f(x), определенной на интервале (–6;
Ответ: 6.
Решение:
Заметим, что производная функции отрицательна, если сама функция f(x) убывает, а значит, необходимо найти количество целых точек, входящих в промежутки убывания функции.
Таких точек 6:
х = −4, х = −3, х = −2,
х = −1, х = 0, х = 3.
–2
–1
–3
–4
0
3
у = f(x)
–6
5
у
х
Слайд 90
у = f(x)
–6
6
у
х
2
4
6
3
5
1
№8
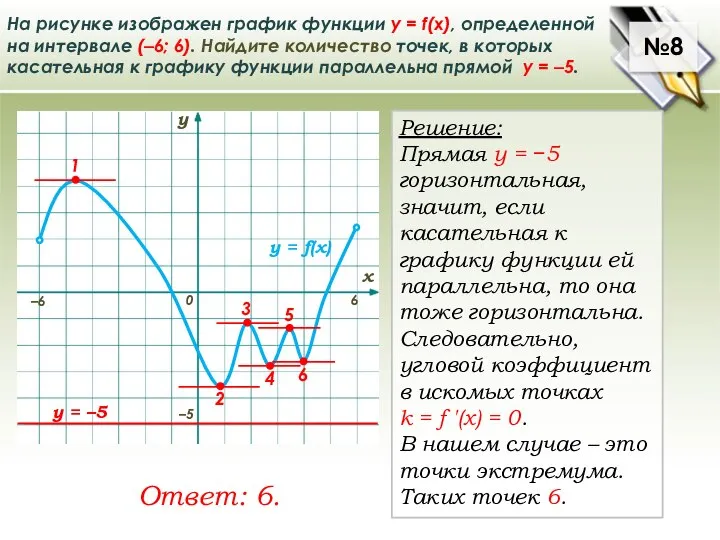
На рисунке изображен график функции у = f(x), определенной
0
у = f(x)
–6
6
у
х
2
4
6
3
5
1
№8
На рисунке изображен график функции у = f(x), определенной
Ответ: 6.
Решение:
Прямая у = −5 горизонтальная, значит, если касательная к графику функции ей параллельна, то она тоже горизонтальна. Следовательно, угловой коэффициент в искомых точках
k = f ′(х) = 0.
В нашем случае – это точки экстремума.
Таких точек 6.
у = –5
–5
Слайд 10№9
На рисунке изображен график у = f(x) – производной функции f(x), определенной на
№9
На рисунке изображен график у = f(x) – производной функции f(x), определенной на
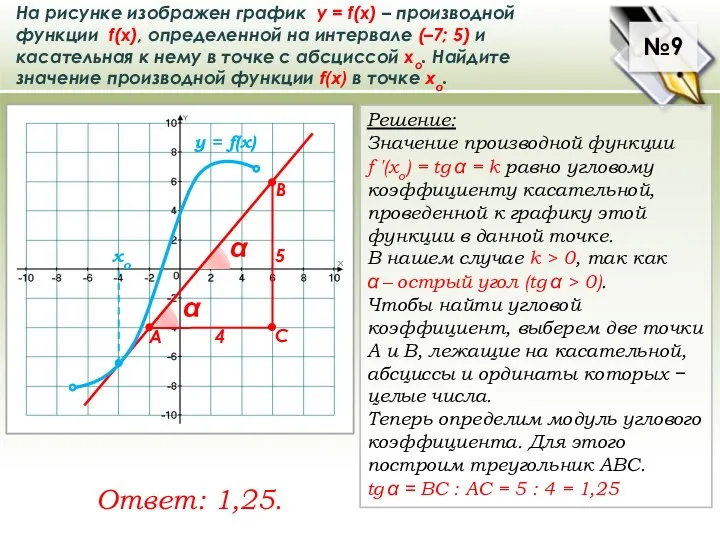
касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(x) в точке хо.
Ответ: 1,25.
Решение:
Значение производной функции
f ′(хo) = tg α = k равно угловому коэффициенту касательной,
проведенной к графику этой функции в данной точке.
В нашем случае k > 0, так как
α – острый угол (tg α > 0).
Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа.
Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC.
tg α = ВС : АС = 5 : 4 = 1,25
у = f(x)
4
А
В
С
5
хо
α
α
Слайд 11180°− α
№10
На рисунке изображен график функции у = f(x), определенной на интервале
180°− α
№10
На рисунке изображен график функции у = f(x), определенной на интервале
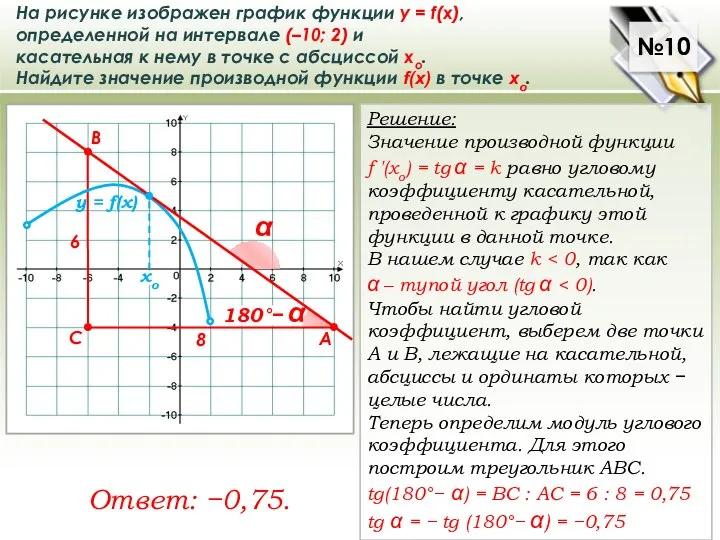
касательная к нему в точке с абсциссой хо.
Найдите значение производной функции f(x) в точке хо.
Ответ: −0,75.
Решение:
Значение производной функции
f ′(хo) = tg α = k равно угловому коэффициенту касательной,
проведенной к графику этой функции в данной точке.
В нашем случае k < 0, так как
α – тупой угол (tg α < 0).
Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа.
Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC.
tg(180°− α) = ВС : АС = 6 : 8 = 0,75
tg α = − tg (180°− α) = −0,75
8
А
В
С
6
хо
α
у = f(x)
Слайд 12.
На рисунке изображен график производной у = f ′(x) –функции f(x), определенной на
.
На рисунке изображен график производной у = f ′(x) –функции f(x), определенной на
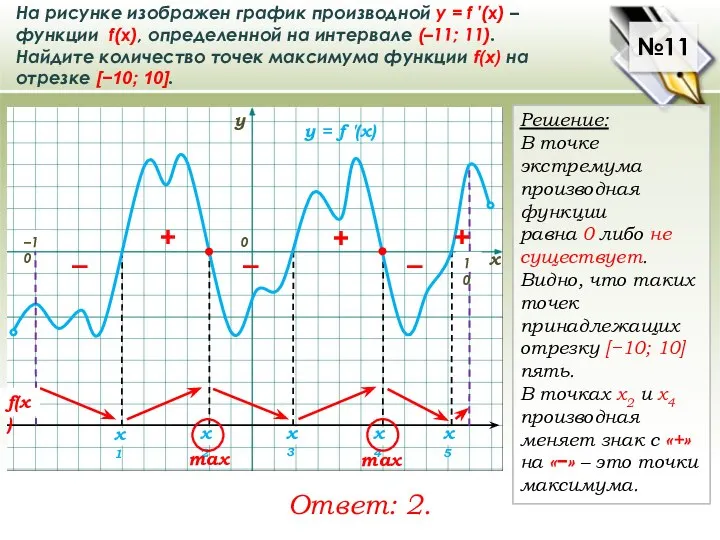
Найдите количество точек максимума функции f(x) на отрезке [−10; 10].
у
х
у = f ′(x)
0
Решение:
В точке экстремума производная функции
равна 0 либо не существует. Видно, что таких точек
принадлежащих отрезку [−10; 10] пять.
В точках х2 и х4 производная меняет знак с «+» на «−» – это точки максимума.
–
+
–
+
–
+
х1
х2
х3
х4
х5
max
max
Ответ: 2.
f(x)
–10
10
№11
Слайд 13Прямая у = 4х – 4 является касательной к графику функции ах2
Прямая у = 4х – 4 является касательной к графику функции ах2

Решение:
Производная функции в точке касания должна совпадать с угловым коэффициентом прямой. Откуда, если за хo принять абсциссу точки касания, имеем: 2ахo + 34 = 4. То есть ахo = –15.
Найдем значение исходной функции в точке касания:
ахo2 + 34хo + 11 = –15xo + 34хo + 11 = 19хo + 11.
Так как прямая у = 4х – 4 – касательная, имеем:
19хo + 11 = 4хo – 4, откуда хo = –1.
А значит a = 15.
Ответ: 15.
№12
Слайд 14Прямая у = – 4х – 5 является касательной к графику функции
Прямая у = – 4х – 5 является касательной к графику функции

Решение.
Если хо – абсцисса точки касания, то 18xo+ b = –4, откуда b = – 4 – 18хо.
Аналогично задаче №12 найдем хо:
9xo2 + (– 4 – 18хо) xo + 20 = – 4хo – 5,
9xo2 – 4xo – 18хо2 + 20 + 4хo + 5 = 0,
– 9xo2 + 25 = 0,
хо2 = 25/9.
Откуда xo = 5/3 или xo = –5/3.
Условию задачи соответствует только положительный корень, значит xo = 5/3, следовательно b = – 4 – 18 ∙ 5/3, имеем b = –34.
Ответ: –34.
№13
Слайд 15Прямая у = 2х – 6 является касательной к графику функции х2
Прямая у = 2х – 6 является касательной к графику функции х2

Решение.
Аналогично предыдущим задачам обозначим абсциссу точки касания хо и приравняем значение производной функции в точке хо угловому коэффициенту касательной.
2хо + 12 = 2, откуда xo = –5.
Значение исходной функции в точке –5 равно:
25 – 60 + с = с – 35, значит с – 35 = 2 ∙ (–5) – 6,
откуда с = 19.
Ответ: 19.
№14
Слайд 16Материальная точка движется прямолинейно по закону
x(t) = 0,5t2 – 2t –
Материальная точка движется прямолинейно по закону
x(t) = 0,5t2 – 2t –

t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с.
Решение.
Так как мгновенная скорость точки в момент времени to, прямолинейного движения, совершаемого по закону х = х(t), равна значению производной функции х npu t = to,
искомая скорость будет равна
x ′(t) = 0,5 ∙ 2t – 2 = t – 2,
x ′(6) = 6 – 2 = 4 м/с.
Ответ: 4.
№15
Слайд 17Материальная точка движется прямолинейно по закону
x(t) = 0,5t2 – 2t –
Материальная точка движется прямолинейно по закону
x(t) = 0,5t2 – 2t –

t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с?
Решение.
Так как мгновенная скорость точки в момент времени to, прямолинейного движения, совершаемого по закону х = х(t), равна значению производной функции х npu t = to,
искомая скорость будет равна
x ′(to) = 0,5 ∙ 2to – 2 = to – 2,
Т.к. по условию, x ′(to) = 4, то to – 2 = 4, откуда
to = 4 + 2 = 6 м/с.
Ответ: 6.
№16
Слайд 18На рисунке изображен график функции у = f(x), определенной на интервале (–8;
На рисунке изображен график функции у = f(x), определенной на интервале (–8;
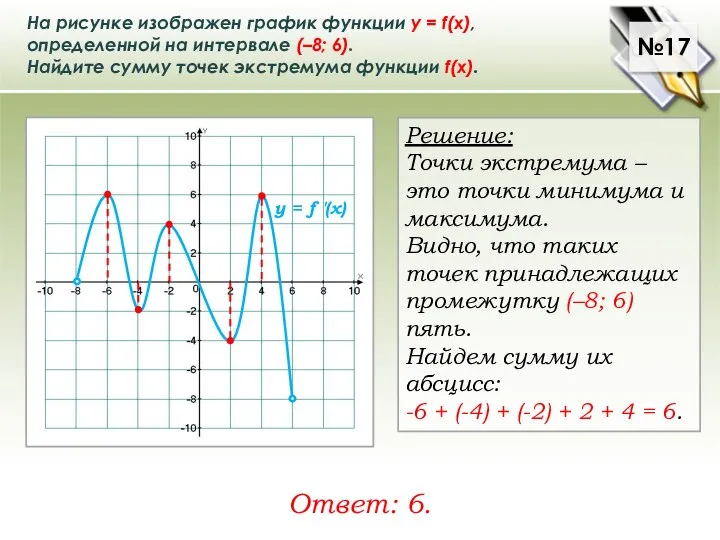
Найдите сумму точек экстремума функции f(x).
Решение:
Точки экстремума – это точки минимума и максимума.
Видно, что таких точек принадлежащих промежутку (–8; 6) пять.
Найдем сумму их абсцисс:
-6 + (-4) + (-2) + 2 + 4 = 6.
Ответ: 6.
№17
у = f ′(x)
Слайд 19На рисунке изображен график производной у = f ′(x) – функции f(x), определенной
На рисунке изображен график производной у = f ′(x) – функции f(x), определенной
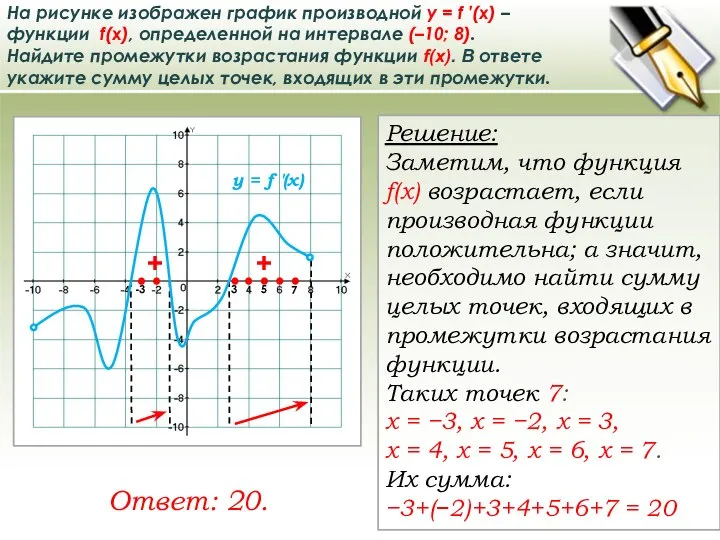
Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
у = f ′(x)
+
+
Решение:
Заметим, что функция f(x) возрастает, если производная функции положительна; а значит, необходимо найти сумму целых точек, входящих в промежутки возрастания функции.
Таких точек 7:
х = −3, х = −2, х = 3,
х = 4, х = 5, х = 6, х = 7.
Их сумма:
−3+(−2)+3+4+5+6+7 = 20
7
5
3
-3
Ответ: 20.
 Признаки параллельности прямых
Признаки параллельности прямых Дифференциальные уравнения
Дифференциальные уравнения Презентация на тему Перпендикулярные прямые (7 класс)
Презентация на тему Перпендикулярные прямые (7 класс)  Разложение на множители с помощью формул квадрата суммы и квадрата разности
Разложение на множители с помощью формул квадрата суммы и квадрата разности Решение задач
Решение задач Дифференциальное исчисление элементарной и сложной функции функции
Дифференциальное исчисление элементарной и сложной функции функции Параллельность прямых
Параллельность прямых Задания по математике (5 класс, часть 3)
Задания по математике (5 класс, часть 3) Задачи на определение ускорения по заданному графику скорости
Задачи на определение ускорения по заданному графику скорости О построении дерева Хаффмана
О построении дерева Хаффмана Множества и отображения
Множества и отображения Obratnye_trigonometricheskie_funktsii (1)
Obratnye_trigonometricheskie_funktsii (1) Тренажер Вычисление производных
Тренажер Вычисление производных История дробей
История дробей Задачи о вкладах и кредитовании (банковских процентах)
Задачи о вкладах и кредитовании (банковских процентах) Влияние математических действий на аликвоты
Влияние математических действий на аликвоты Диференціальні рівняння
Диференціальні рівняння Наибольшее наименьшее значение функции на промежутке. Примеры использования производной для нахождения наилучшего решения
Наибольшее наименьшее значение функции на промежутке. Примеры использования производной для нахождения наилучшего решения Види кутів
Види кутів Алгебраические уравнения. (Лекция 1)
Алгебраические уравнения. (Лекция 1) Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед
Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед Числа 6 и 7. Письмо цифры 6
Числа 6 и 7. Письмо цифры 6 Метод рационализации в логарифмических неравенствах
Метод рационализации в логарифмических неравенствах Презентация на тему Понятие движения
Презентация на тему Понятие движения  Признаки подобия треугольников
Признаки подобия треугольников Многовариантные планиметрические задачи: взаимное расположение фигур
Многовариантные планиметрические задачи: взаимное расположение фигур Устный счёт
Устный счёт Занимательная математика
Занимательная математика