Слайд 2Понятие БО
БО – всякое подмножество прямого произведения А × В
ПРИМЕР. Пусть

А = {2; 3}, B = {3; 4; 5; 6},
тогда А × В = {(2; 3); (2; 4); (2; 5); (2; 6); (3; 3); (3; 4); (3; 5); (3; 6)}
Рассмотрим БО R – «быть делителем»
R = {(2; 4); (2; 6); (3; 3); (3; 6)}
• Dom R – область определения
{2; 3} – подмножество А
• Im R – область значений
{3; 4; 6} – подмножество В
Слайд 3Основные способы задания БО
Перечислением элементов R = {(2; 4); (2; 6); (3;

3); (3; 6)}
Указанием характеристического свойства R = {(a; b)| a - делитель b}
Слайд 4Операции над БО
Обращение отношения (инверсия)
Переход от R к R-1 осуществляется

взаимной перестановкой координат каждой упорядоченной пары. При этом область определения становится областью значений и наоборот.



 Скалярное прозведение векторов
Скалярное прозведение векторов Решение задач
Решение задач Преобразования графиков функций. 8 класс
Преобразования графиков функций. 8 класс Признаки параллельности прямых. Тест
Признаки параллельности прямых. Тест Лекция_04
Лекция_04 Среднее арифметическое
Среднее арифметическое Квадратичная зависимость
Квадратичная зависимость Логарифмы вокруг нас
Логарифмы вокруг нас Диофантово уравнение
Диофантово уравнение Проценты
Проценты Задачи на построение сечений
Задачи на построение сечений Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Интегралы. Введение в математический анализ
Интегралы. Введение в математический анализ Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Названия чисел в записях действий
Названия чисел в записях действий Основные формулы
Основные формулы Задачи на совместную работу
Задачи на совместную работу Проверка деления
Проверка деления Презентация на тему Треугольники. Третий признак равенства
Презентация на тему Треугольники. Третий признак равенства  Математическая статистика 2
Математическая статистика 2 Факториал. Задача со стульями
Факториал. Задача со стульями Геометричне моделювання організаційних кластерних сруктур
Геометричне моделювання організаційних кластерних сруктур Логарифмы. Возведение в степень. Логарифмирование
Логарифмы. Возведение в степень. Логарифмирование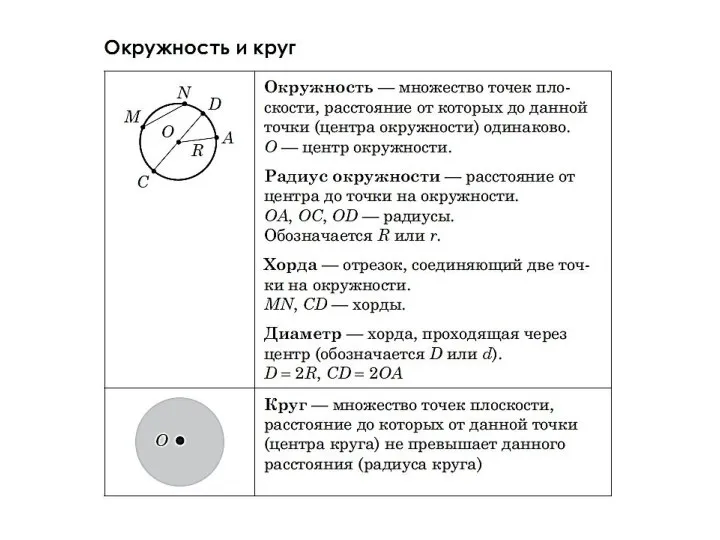 Окружность и круг
Окружность и круг Презентация на тему Решение систем линейных уравнений 7 класс для учителя
Презентация на тему Решение систем линейных уравнений 7 класс для учителя  Метод Крамера
Метод Крамера Презентация на тему Зарождение и история геометрии
Презентация на тему Зарождение и история геометрии