Числа. Комплексные числа

Конец

Натуральные N
— это числа, которые используют при счете предметов.
Пример: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11 и т.д.
Свойства

Схема

1. Сумма целых чисел.
Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.
Пример: (+2) + (+5) = +7.
2. Вычитание целых чисел.
Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.
Пример: (–2) + (+5) = +3.
3. Умножение целых чисел.
Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.
Пример:(+2) ∙ (–3) = –6.
Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.
Пример: (–2) ∙ (+3) ∙ (–5) ∙ (–3) ∙ (+4) = –360 (3 неположительных сомножителя).
4. Деление целых чисел.
Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, – если разные.
Пример: (–12) : (+6) = –2.
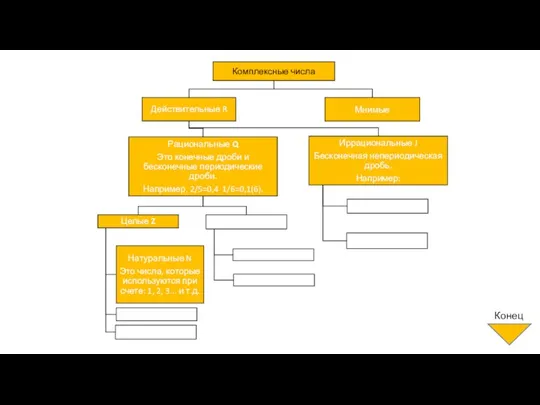
Схема

Рациональное число Q
Представление

Любое рациональное число можно представить в виде десятичной дроби, либо в виде периодической десятичной дроби
Свойства

Распределительное свойство умножения относительно сложения
Схема
Распределительное свойство умножения справедливо и в обратную сторону.
Такое преобразование выражения называют вынесением общего множителя за скобки.