Содержание
- 2. Метод Гаусса решения систем линейных уравнений Рассмотрим задачу решения системы линейных уравнений размерностью (m x n).
- 3. Метод Гаусса решения систем линейных уравнений Следующие действия над расширенной матрицей системы называются элементарными преобразованиями. Умножение
- 4. Метод Гаусса решения систем линейных уравнений Запишем расширенную матрицу системы К первой строке прибавим вторую строку,
- 6. Скачать презентацию



 Разделите выражения на группы
Разделите выражения на группы Решение заданий повышенной сложности
Решение заданий повышенной сложности Тригонометрические уравнения
Тригонометрические уравнения Измерение массы (для детей 6 лет)
Измерение массы (для детей 6 лет) Вычисление дробей. Устная работа
Вычисление дробей. Устная работа УК Теория и примеры типовых задач. Проверка (испытание) гипотез
УК Теория и примеры типовых задач. Проверка (испытание) гипотез Методы решения типовых задач по специальной теории относительности
Методы решения типовых задач по специальной теории относительности Множества
Множества Вписанная и описанная окружность
Вписанная и описанная окружность Презентация на тему Правила вычисления производных
Презентация на тему Правила вычисления производных  Точка. Кривая линия. Прямая линия. Отрезок. Луч. Ломаная линия
Точка. Кривая линия. Прямая линия. Отрезок. Луч. Ломаная линия Геометрия вокруг нас
Геометрия вокруг нас Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Преобразование графиков
Преобразование графиков Множества натуральных чисел
Множества натуральных чисел Презентация на тему Н.И. Лобачевский и проблемы образования
Презентация на тему Н.И. Лобачевский и проблемы образования  Тригонометрия. Измерение угловых величин
Тригонометрия. Измерение угловых величин Конус
Конус Логические задачки для дошкольников
Логические задачки для дошкольников Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Площадь параллелограмма
Площадь параллелограмма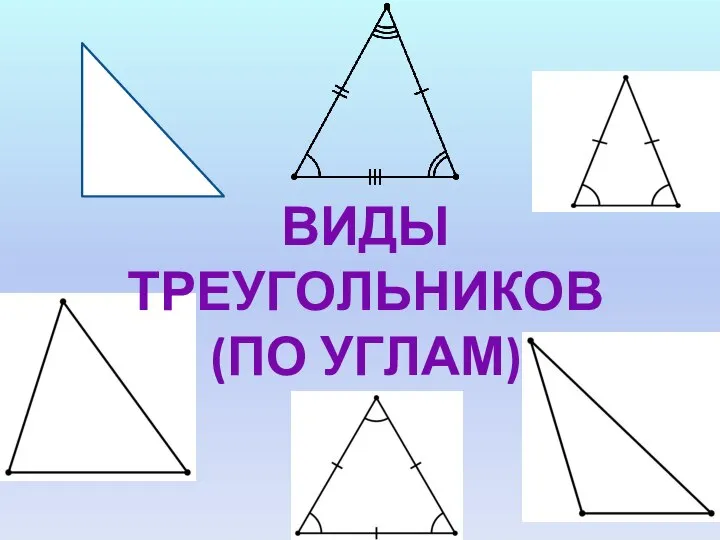 Виды треугольников по углам
Виды треугольников по углам Презентация на тему В царстве квадратных корней
Презентация на тему В царстве квадратных корней  Презентация на тему Длина окружности. Площадь круга
Презентация на тему Длина окружности. Площадь круга  Презентация по математике "Чтение и запись натуральных чисел. Разряд" -
Презентация по математике "Чтение и запись натуральных чисел. Разряд" -  Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ  Понятие и чертёж, элементы призмы
Понятие и чертёж, элементы призмы