Содержание
- 2. Цель лекции: 1. Сформулировать основные определения. 2. Изучить законы распределения случайных вели-чин и случайных процессов. 3.
- 4. Законы распределения полностью характеризуют слу-чайную величину с вероятностной точки зрения. Зная закон распределения, можно указать возможные
- 5. 3. Имеются законы распределения, которые характери-зуются несколькими параметрами. Знание этих парамет-ров достаточно, чтобы определить закон распределения.
- 6. 2.1. Математическое ожидание Математическое ожидание является важнейшей хара-ктеристикой случайной величины. Ее еще называют сред-ним значением случайной
- 8. 1. Математическое ожидание дискретной случайной величины где xi − i-ое значение случайной величины ; Pi −
- 9. 3. Если случайная величина Y является функцией слу-чайной величины X, т.е. y = f(x), то математическое
- 10. 2. Дисперсия непрерывной случайной величины 3. Если случайная величина Y является функцией слу-чайной величины X, т.е.
- 11. 2.3. Моменты случайной величины На практике применяют моменты двух видов: началь-ные моменты и центральные моменты. Таким
- 12. Начальным моментом k-го порядка непрерывной слу-чайной величины X называется математическое ожидание случайной величины Y, значения которой
- 13. Очевидно, что центральный момент первого порядка равен нулю: В свою очередь, центральный момент второго порядка есть
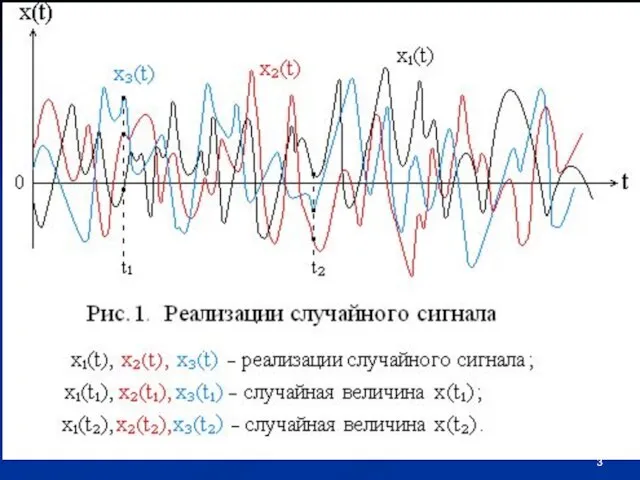
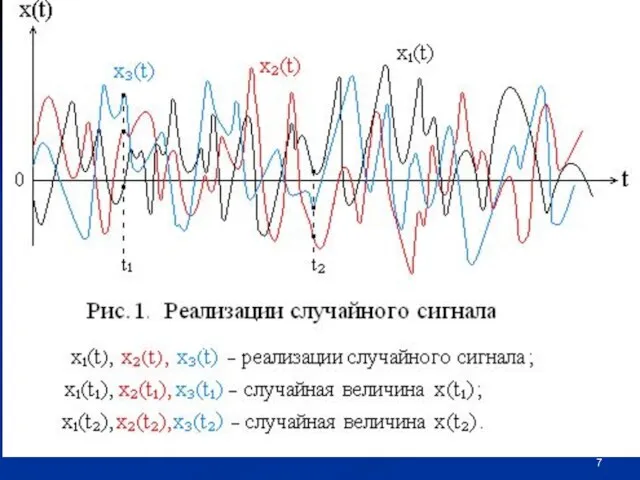
- 14. 3. Числовые характеристики случайных сигналов Прежде чем рассматривать числовые характеристики случайных сигналов, необходимо определить разновидно-сти случайных
- 15. 3.1. Стационарные случайные процессы Стационарные случайные процессы – это важнейший класс случайных процессов, которые являются матема-тической
- 16. Другими словами, у стационарного в узком смысле слу-чайного процесса n-мерные плотности вероятности при всех n инвариантны
- 17. Приведем формулы для числовых характеристик неста-ционарного и стационарного случайных процессов. а. Нестационарный случайный процесс Дисперсия Ковариационная
- 18. Дисперсия Ковариационная функция Корреляционная функция Математическое ожидание б. Стационарный случайный процесс
- 19. Для стационарных случайных сигналов можно выдели-ть следующие свойства числовых характеристик. 1. Корреляционная функция стационарного процесса четная,
- 20. Докажем это. Определим математическое ожидание полагая, что mx = 0. Таким образом,
- 21. Большинство стационарных случайных процессов обла-дают очень важным для практики свойством эргодично-сти. Суть этого свойства заключается в
- 22. Стационарный случайный процесс называется эргоди-ческим, если при определении его статистических харак-теристик усреднение по множеству реализаций эквива-лентно
- 23. Дисперсия Ковариационная функция Корреляционная функция Математическое ожидание
- 24. 3.3. Взаимная корреляционная функция Пусть x(t) и y(t) стационарные и стационарно связанные случайные процессы. Взаимные ковариационная
- 25. Рассмотрим два эргодических случайных процесса x(t) и y(t) с математическими ожиданиями, равными 0. Корре-ляционная функция случайного
- 26. Выводы. 1. Обоснована необходимость определения числовых характеристик случайных величин и случайных процес-сов. 2. Дано определение стационарных
- 27. 2.4. Корреляционные моменты двух случайных величин Для количественной меры статистических связей двух случайных величин применяют смешанный
- 29. Простейшие преобразования позволяют установить сле-дующую связь между Bxy и Rxy. Свойства корреляционного момента. 1. Корреляционный момент
- 30. Тогда 2. При Rxy 0 ) между величинами X и Y су-ществует отрицательная (положительная) корреляционная зависимость,
- 32. Скачать презентацию
























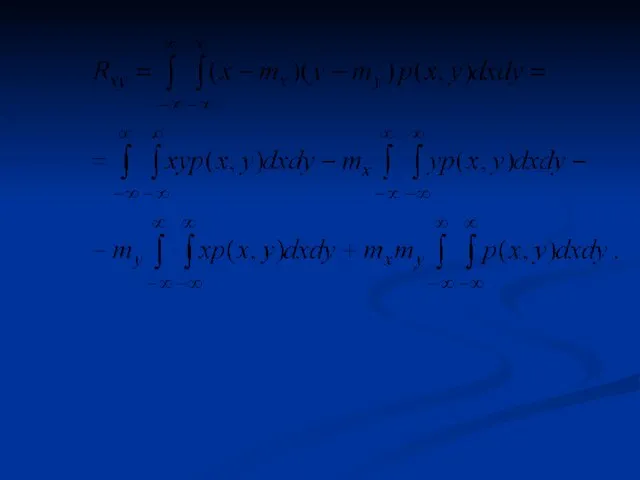


 Technologia informacyjna
Technologia informacyjna Нахождение дроби от числа и числа по его дроби. Ответь на вопросы
Нахождение дроби от числа и числа по его дроби. Ответь на вопросы Вычисление производной
Вычисление производной Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Виды треугольников
Виды треугольников Задача на внимание. 5 класс
Задача на внимание. 5 класс Угол. Виды углов
Угол. Виды углов Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Теоремы синусов и косинусов. Тест
Теоремы синусов и косинусов. Тест Смежные и вертикальные углы
Смежные и вертикальные углы Диагностическая работа по математике (октябрь)
Диагностическая работа по математике (октябрь) Презентация на тему Квадратный корень. Арифметический квадратный корень
Презентация на тему Квадратный корень. Арифметический квадратный корень  Презентация на тему Признаки параллельности прямых
Презентация на тему Признаки параллельности прямых  Третий признак равенства треугольников
Третий признак равенства треугольников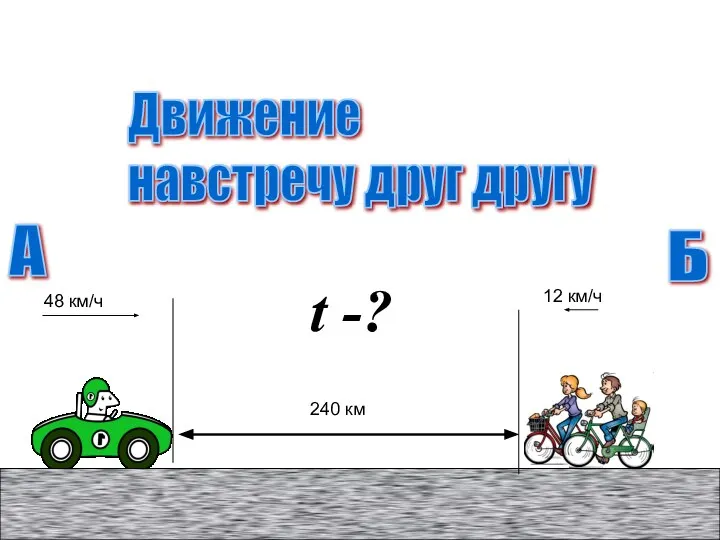 Задачи на движение
Задачи на движение Фундаментальная система решений (ФСР)
Фундаментальная система решений (ФСР) Обобщение и систематизация знаний по главе 10. Метапредмет – задача
Обобщение и систематизация знаний по главе 10. Метапредмет – задача Дроби
Дроби Логика Закон тождества
Логика Закон тождества Тени основных геометрических фигур (по одной проекции)
Тени основных геометрических фигур (по одной проекции) Осевая симметрия
Осевая симметрия Презентация на тему Нумерация многозначных чисел (4 класс)
Презентация на тему Нумерация многозначных чисел (4 класс)  Использование прикладных программ для оптимизации задач исследования. Контрольная работа
Использование прикладных программ для оптимизации задач исследования. Контрольная работа Деление с остатком
Деление с остатком Подготовка к контрольной работе №4. 5 класс
Подготовка к контрольной работе №4. 5 класс Игра Что? Где? Почему?
Игра Что? Где? Почему? Выбор рационального пути решения задач
Выбор рационального пути решения задач Математика в нашей жизни
Математика в нашей жизни