Чётность и нечётность, периодичность тригонометрических функций с изменениями

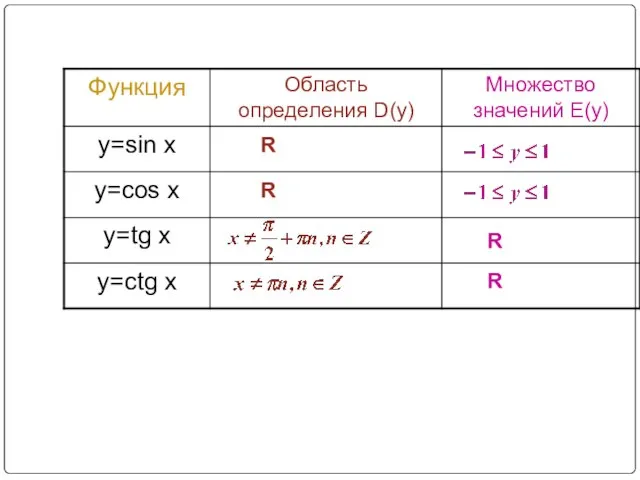
Новый материал
R
R
R
R

Решение упражнений
1. Найдите область определения функции:

Решение упражнений
3. Найдите область определения функции:
Решение
•
-1
°
0
0
π

Решение упражнений
3. Найдите область определения функции:

11 класс
Четность и нечетность тригонометрических функций

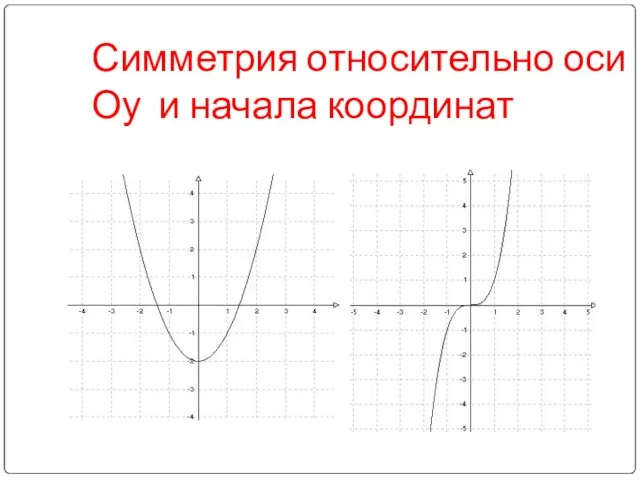
Симметрия относительно оси Оу и начала координат

Четные функции
Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x).
Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную(–x).

Четные функции
Например: является ли четной функция f(x) = 3x2 + 2
f(-x) = 3(-x)2 + 2 = 3x2 + 2 = f(x) – функция четная

Четные функции
f(x) = 2x4 - 3x2
f(x) = x3 - 2x2
f(-x) = 2(-x)4 – 3(-x)2 = 2x4 - 3x2 - четная
f(-x) = (-x)3 – 2(-x)2 = – x3 – 2x2 Не является четной
Проверим являются ли данные функции четными

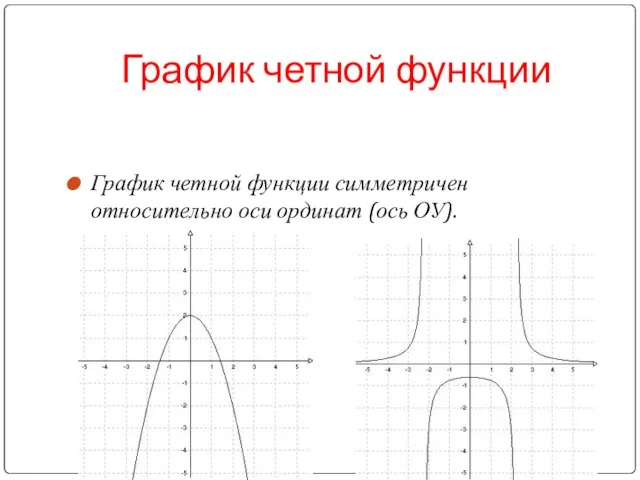
График четной функции
График четной функции симметричен относительно оси ординат (ось ОУ).

Нечетные функции
Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство
f(-x) = - f(x).
чтобы узнать является ли функция нечетной нужно в функцию f(x) вместо переменной х поставить переменную (–x) и получить первоначальную функцию с противоположными знаками.

Нечетные функции
Например: является ли нечетной функция f(x) = 3x3 + х
f(-x) = 3(-x)3 + (-х) = -3x3 - х = -(3x3 + х)=
= - f(x) – функция нечетная

Нечетные функции
f(x) = 2x4 + 3x
f(x) = x3 - 2x
f(-x) = 2(-x)4 + 3(-x) = =2x4 - 3x - не является нечетной
f(-x) = (-x)3 – 2(-x) = – x3 + 2x нечетная
Проверим являются ли данные функции нечетными

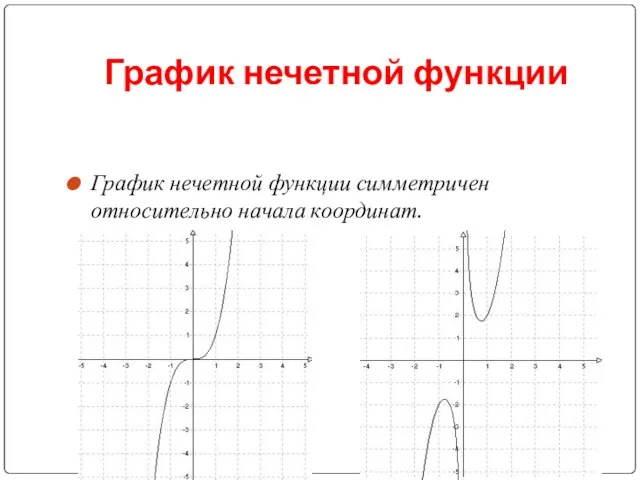
График нечетной функции
График нечетной функции симметричен относительно начала координат.

Четные и нечетные функции
Функции могут быть как четными, нечетными, так и ни четными, ни нечетными.
Пример: y(x) = x2 + 2x
y(-x) = (-x)2 + 2(-x) = x2 - 2x

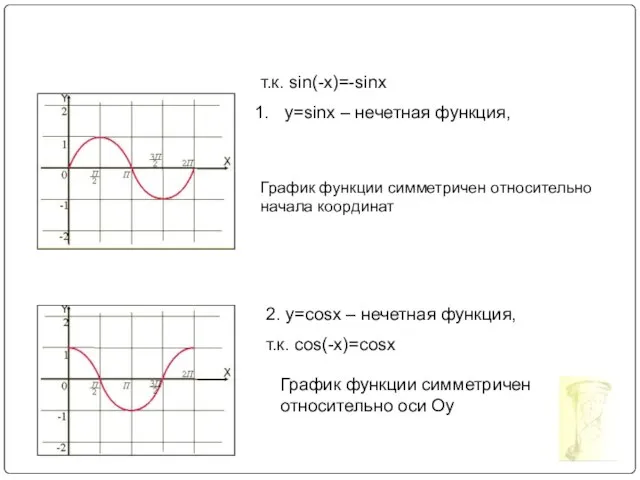
Для любого значения x верны равенства:
Sin(-x) = -Sin x
Cos(-x) = Cos x
Следовательно:
y= Sin x – нечетная функция
y= Cos x – четная функция
Четность и нечетность

т.к. sin(-x)=-sinx
y=sinx – нечетная функция,
График функции симметричен относительно начала координат
2. y=cosx – нечетная функция,
т.к. cos(-x)=cosx
График функции симметричен относительно оси Оу

Так как для любого значения x из области определения функции
y = tg x верно равенство
tg(-x) = -tg x,
то y = tg x – нечетная функция.

Пример
Выяснить, является ли функция
y = 2 + Sin2 x четной или нечетной.
Решение:
y(-x) = 2 + Sin2(-x) = 2 + (-Sin x)2 =
=2 + Sin2x = y(x) ?
?y = 2 + Sin2x – четная функция.

Пример: определите, является ли данная функция четной или нечетной
Решение:

Работа в тетрадях
Определите, являются ли данные функции четными или нечетными:

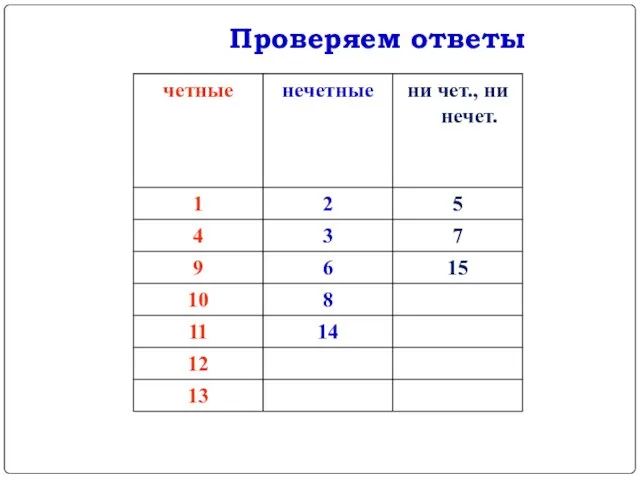
Разбейте функции на три группы:
четные
нечетные
не являются ни четными, ни нечетными

Проверяем ответы

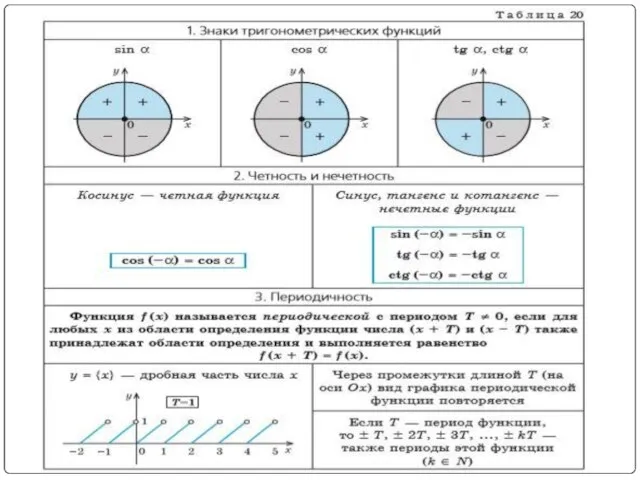
Функция f(x) называется периодической, если существует такое число T ≠ 0, что для любого x из области определения этой функции выполняется равенство
f(x – T) = f(x) = f(x + T).
Число T называется периодом функции f(x).
!Определение!

Для любого значения x верны равенства:
Sin (x + 2π) = Sin x
Cos (x + 2π) = Cos х
Следовательно, значения Sin и Cos периодически повторяются при изменении аргумента на 2π.
Такие функции называются периодическими с периодом 2π.
Периодичность

Покажем, что число 2π является наименьшим положительным периодом функции y = Cos x.
Пусть Т › 0 – период косинуса, т.е. для любого x выполняется равенство
Cos (x + T) = Cos x. Положив x = 0, получим Cos T = 1. Отсюда T = 2πk, k є Ζ. Так как Т › 0, то Т может принимать значения 2π, 4π, 6π, …, и поэтому период не может быть меньше 2π.

Аналогично можно доказать, что наименьший положительный период функции y = Sin x также равен 2π
Пример:
Доказать, что f(x) = Sin 3x – периодическая функция с периодом (2π)/3.
Доказательство:
Данная функция определена для всех x є R, поэтому достаточно показать, что для любого x верно равенство f(x + T) = f(x).
f(x + (2π)/3) = Sin 3(x + (2π)/3) =
= Sin (3x + 2π) = Sin 3x = f(x)

Покажем, что функция y= tg x является периодической с периодом π.
Если x принадлежит области определения этой функции, т.е. x ≠ -π/2 + πn, n є Ζ, то по формулам приведения получаем
tg(x – π) = -tg(π – x) = -(-tg x) = tg x
tg(x + π) = tg x
Таким обтазом, tg(x – π) = tg x = tg(x + π). Следовательно, π – период функции у = tg x.

Покажем, что π – наименьший положительный период функции y = tg x.
Пусть Т – период тангенса, тогда tg(x + T) = tg x, откуда при x = 0 получаем tg T = 0, T = kπ, k є Ζ. Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции y = tg x.