Содержание
- 2. Многочлен ax2+bx+c называют квадратным трехчленом а – первый (старший) коэффициент b – второй коэффициент (коэффициент при
- 3. - неприведенное квадратное уравнение. - приведенное квадратное уравнение. Определение 3: Полное квадратное уравнение – это квадратное
- 4. Определение 4: Корнем квадратного уравнения ax2+bx+c=0 называют всякое значение переменной х, при котором квадратный трехчлен ax2+bx+c
- 5. Пример 1: Решить неполное квадратное уравнение Если произведение равно нулю, то среди множителей есть хотя бы
- 6. Определение Полным квадратным уравнением называется Числа а, в, с – это коэффициенты квадратного уравнения а –
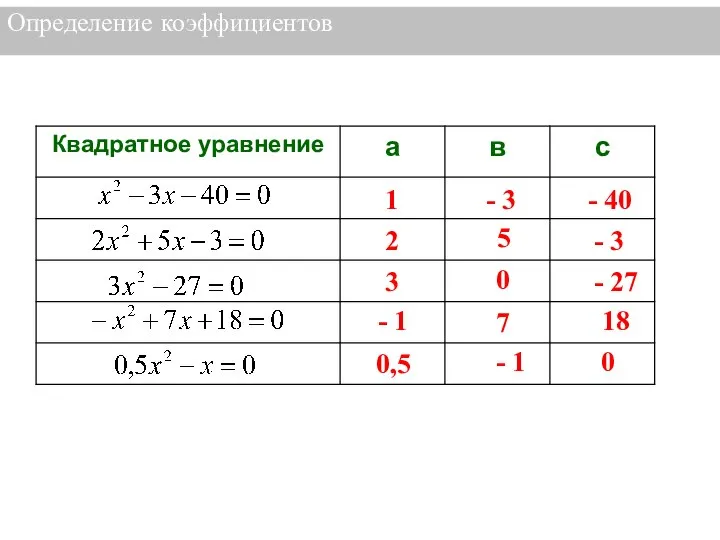
- 7. Определение коэффициентов 1 - 3 - 40 2 5 - 3 3 0 - 27 -
- 8. Решение квадратного уравнения по формуле Алгоритм решения квадратного уравнения вида , где по формуле Находят дискриминант
- 9. Пример: Решить уравнение 3х2+8х-11=0. Решение:
- 10. Примеры: Решить уравнение: Решение:
- 11. Уравнение корней не имеет Пример: Решить уравнение:
- 12. - КОРНЕЙ НЕТ - ОДИН КОРЕНЬ - ДВА КОРНЯ
- 13. Решение квадратного уравнения по свойству коэффициентов: 1 – 2013 : 3 = – 671
- 14. Решение по формуле Решение: а = 3, в = 2010, с = - 2013 Ответ:
- 15. Решите устно квадратные уравнения, используя свойство коэффициентов: Решение квадратного уравнения по свойству коэффициентов:
- 17. Скачать презентацию













 Ступени
Ступени Алгебра высказываний
Алгебра высказываний Интегрированный урок: Многогранники вокруг нас
Интегрированный урок: Многогранники вокруг нас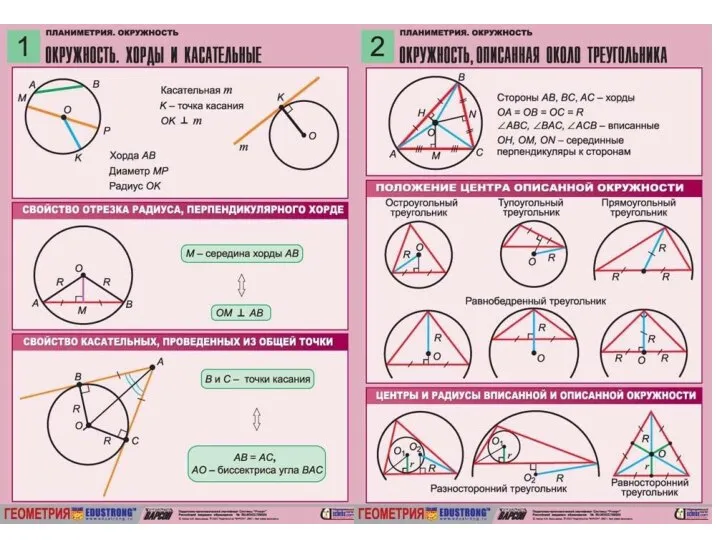 Геометрия. Конспекты
Геометрия. Конспекты Координатные векторы
Координатные векторы Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами Векторы. Задания
Векторы. Задания Усный счет
Усный счет Построение сечений
Построение сечений Квадратичная функция. Урок алгебры в 8 классе
Квадратичная функция. Урок алгебры в 8 классе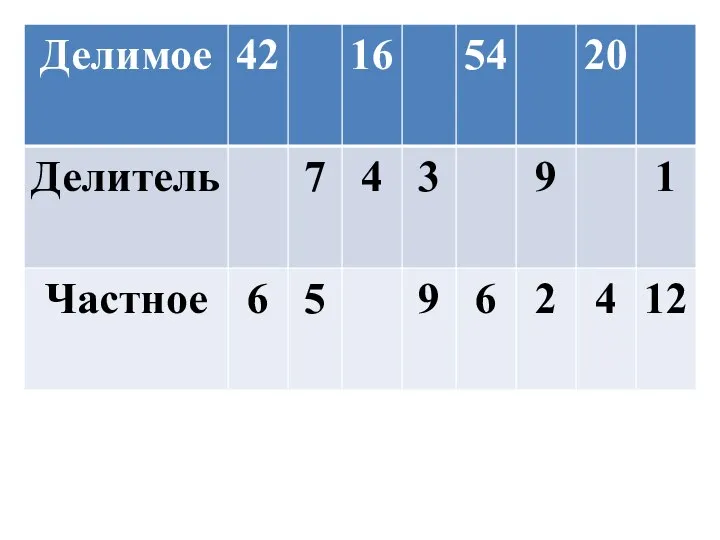 Таблица умножения и деления
Таблица умножения и деления Куб. Формулы для куба
Куб. Формулы для куба Задачки со всего света. Проект Секреты чисел. Команда Искорка
Задачки со всего света. Проект Секреты чисел. Команда Искорка Алгебра в нашей жизни
Алгебра в нашей жизни Свойства числовых функций
Свойства числовых функций Проценты
Проценты Решение задач по теме: Прямоугольник. Ромб. Квадрат
Решение задач по теме: Прямоугольник. Ромб. Квадрат Математическое моделирование
Математическое моделирование Софт- портфель учителя
Софт- портфель учителя Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Сложение в пределах 20. Тренажёр
Сложение в пределах 20. Тренажёр Игра по станциям математический турнир. 7 класс
Игра по станциям математический турнир. 7 класс Решение квадратных уравнений
Решение квадратных уравнений Вычитание двузначных чисел с переходом в другой разряд
Вычитание двузначных чисел с переходом в другой разряд Дифференцирование показательной и логарифмической функций
Дифференцирование показательной и логарифмической функций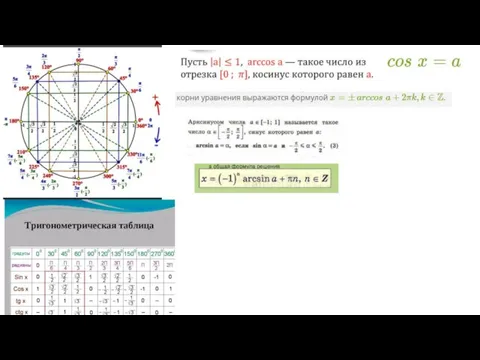 Тригонометрические неравенства
Тригонометрические неравенства Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости