d9d859ec9ada2cfd333ac86c8bdd6908

1.Выявить свойства чисел, входящих в состав треугольника Паскаля
2. Определить применение свойств чисел треугольника Паскаля
3. Сформулировать вывод и итоги исследования
ЗАДАЧИ ИССЛЕДОВАНИЯ

Привести достаточное количество
примеров свойств чисел треугольника
Паскаля и примеров применения
треугольника для доказательства
гипотезы.
ЦЕЛЬ ИССЛЕДОВАНИЯ

Если числа
треугольника Паскаля
обладают особыми
свойствами,
то его
можно считать
волшебным.
ГИПОТЕЗА

ХОД ИССЛЕДОВАНИЯ
Собрать первоначальные сведения о треугольнике в энциклопедической и учебно-научной литературе.
Выяснить, что высказывали о треугольнике Паскаля ученые или математики.

Мартин Гарднер
"Математические новеллы"
1974
"Треугольник Паскаля так прост,
что выписать его сможет даже
десятилетний ребенок.
В тоже время он таит в себе
неисчерпаемые сокровища и связывает
воедино различные аспекты математики,
не имеющие на первый взгляд между
собой ничего общего.
Столь необычные свойства позволяют
считать треугольник Паскаля одной из
наиболее изящных схем
во всей математике".

ТРЕУГОЛЬНИК ПАСКАЛЯ
—это бесконечная числовая таблица
"треугольной формы", в которой по боковым
сторонам стоят единицы и всякое число,
кроме этих боковых единиц.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
. . . . . . . . . . . . . . .
ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА

ХОД ИССЛЕДОВАНИЯ
Выявить самые «Волшебные» свойства чисел треугольника
Выяснить, какими еще свойствами обладает треугольник Паскаля

Каждое число
равно сумме двух
расположенных
над ним чисел.
САМЫЕ ВОЛШЕБНЫЕ СВОЙСТВА
Треугольник можно продолжать неограниченно.

Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А.
ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА
Свойство 2: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются).

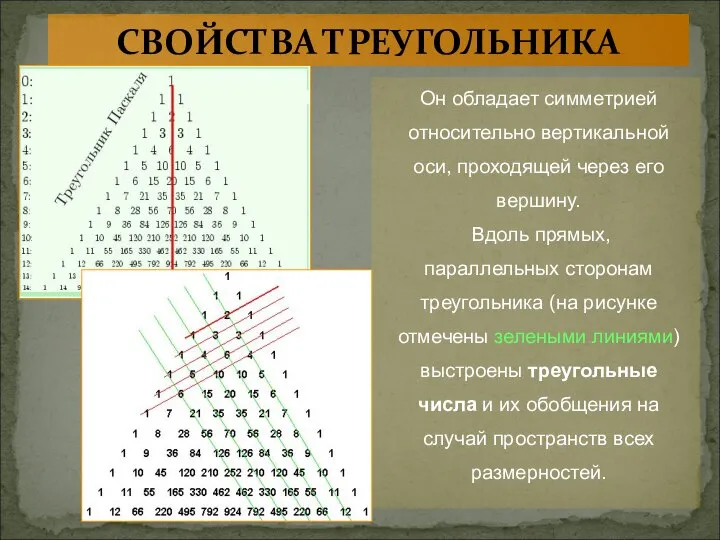
Он обладает симметрией
относительно вертикальной
оси, проходящей через его
вершину.
Вдоль прямых,
параллельных сторонам
треугольника (на рисунке
отмечены зелеными линиями)
выстроены треугольные
числа и их обобщения на
случай пространств всех
размерностей.
СВОЙСТВА ТРЕУГОЛЬНИКА

Треугольные числа показывают, сколько касающихся кружков можно расположить в виде треугольника
СВОЙСТВА ТРЕУГОЛЬНИКА
Классический пример начальная расстановка шаров в бильярде.
Треугольник Паскаля

Следующая зеленая
линия покажет нам
тетраэдральные числа
- один шар мы можем
положить на три –
итого четыре, под три
подложим шесть
итого десять, и так
далее.
СВОЙСТВА ТРЕУГОЛЬНИКА

Следующая зеленая
линия продемонстрирует
попытку выкладывания
гипертетраэдра в
четырехмерном
пространстве - один шар
касается четырех, а
те, в свою очередь,
десяти...
СВОЙСТВА ТРЕУГОЛЬНИКА

Хотя… Попробуйте с вишнями или яблоками одинакового размера, только не пытайтесь выйти с ними в четвертое измерение, они могут
В нашем мире такое невозможно, только в
четырехмерном, виртуальном. И тем более
пятимерный тетраэдр, о котором
свидетельствует
следующая зеленая линия, он может существовать только в рассуждениях
топологов… или фантастов.
ЗАМЕЧАНИЕ АВТОРА
исчезнуть.

Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии - сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц - это тоже треугольные числа в нульмерном пространстве - сколько бы шаров мы не взяли - больше одного расположить не сможем, ибо просто негде - нет ни длины, ни ширины, ни высоты.
НАВЕРНОЕ ВЫ ХОТИТЕ СПРОСИТЬ…
А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда?

Заменим каждое число в
треугольнике Паскаля точкой.
Причем, нечетные точки
выведем контрастным цветом,
а четные - прозрачным, или
цветом фона.
Результат
окажется непредсказуемо-
удивительным: треугольник
Паскаля разобьется на более
мелкие треугольники,
образующие изящный узор.
Удивительное свойство треугольника Паскаля

ХОД ИССЛЕДОВАНИЯ
Изучить возможности применения треугольника Паскаля
Продемонстрировать примеры

ПРИМЕНЕНИЕ
Пусть, например, мы хотим
вычислить сумму чисел
натурального ряда от 1 до 9.
"Спустившись" по диагонали
До числа 9, мы увидим слева
снизу от него число 45.
Оно то и дает искомую сумму.

ПРИМЕНЕНИЕ
Биномиальные коэффициенты есть
коэффициэнты разложения многочлена
по степеням x и y

Предположим , что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен. Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35.
ПРИМЕНЕНИЕ
Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться!

ХОД ИССЛЕДОВАНИЯ
Формулируем итоги и выводы