Содержание
- 2. Три пути ведут к знанию: -Путь размышления самый благородный, -Путь подражания самый легкий -И путь опыта
- 3. ВОПРОС -ОТВЕТ Что называют одночленом? Какие слагаемые называются подобными? Что называют многочленом? Как умножить степени с
- 4. (a + b)2=a2+2ab+b2 (a - b)2=a2-2ab+b2
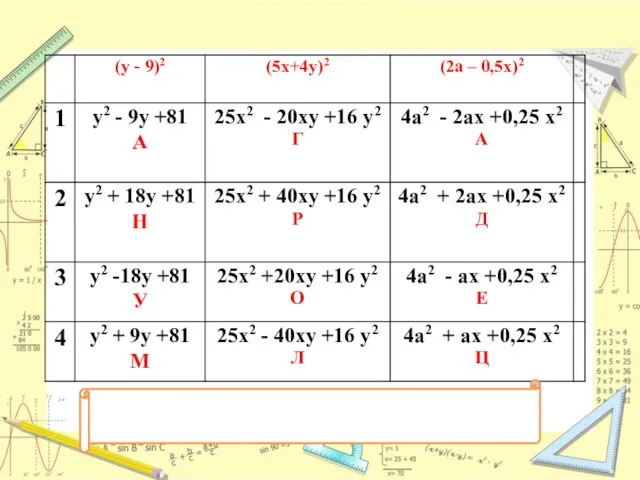
- 5. У Р А
- 6. Представить в виде многочлена:
- 7. Представить в виде многочлена:
- 8. Разность квадратов двух выражений Левую и правую части можно поменять местами, тогда получаем: Формула «разность квадратов»
- 9. Первичное закрепление нового материала Разложи на множители: 1) b² - d² 2) х² - 1 3)
- 10. Первичное закрепление нового материала Разложите на множители, пользуясь формулой разности квадратов : а) (х+2)²-49 = б)
- 11. Выполните умножение многочленов, используя формулу разности квадратов: а) (x+2)(x-2) б) (y+3)(y-3) в) (2x-3y)(2x+3y) г) (3a-5b)(3a+5b) д)
- 12. Домашнее задание а) (x+2)(x-2) б) (y+3)(y-3) в) (2x-3y)(2x+3y) г) (3a-5b)(3a+5b) д) (a²-5)(5+a²) е) (b²+4)(4-b²) Выполните умножение
- 13. Мало иметь хороший ум, главное – уметь его применять Рене Декарт — (1596-1650) — французский философ,
- 15. Скачать презентацию









 Задачи на смеси
Задачи на смеси Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Тест. Свойство простейших фигур
Тест. Свойство простейших фигур Умножение и деление десятичных дробей на двузначное число
Умножение и деление десятичных дробей на двузначное число Построение таблиц истинности
Построение таблиц истинности Провешивание прямой на местности
Провешивание прямой на местности Эти годы позабыть нельзя. Интегрированный урок
Эти годы позабыть нельзя. Интегрированный урок Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Линейное пространство. N-мерные векторы и действия над ними. Тема 1
Линейное пространство. N-мерные векторы и действия над ними. Тема 1 Сопоставимость показателей. Лекция 2
Сопоставимость показателей. Лекция 2 Презентация на тему Изображение пространственных фигур
Презентация на тему Изображение пространственных фигур  Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Деление дробей. Делимое. Взаимо обратные
Деление дробей. Делимое. Взаимо обратные Переместительный закон умножения
Переместительный закон умножения Векторы. Понятие вектора
Векторы. Понятие вектора Счёт до 9. Состав числа 9
Счёт до 9. Состав числа 9 Задачи приводящие к понятию производной
Задачи приводящие к понятию производной Использование параллелограмма в жизни
Использование параллелограмма в жизни Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями
Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями Презентация на тему Деление суммы на число (3 класс)
Презентация на тему Деление суммы на число (3 класс)  Целое уравнение
Целое уравнение II АПТА Практикалық сабаққа тапсырмалар
II АПТА Практикалық сабаққа тапсырмалар Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление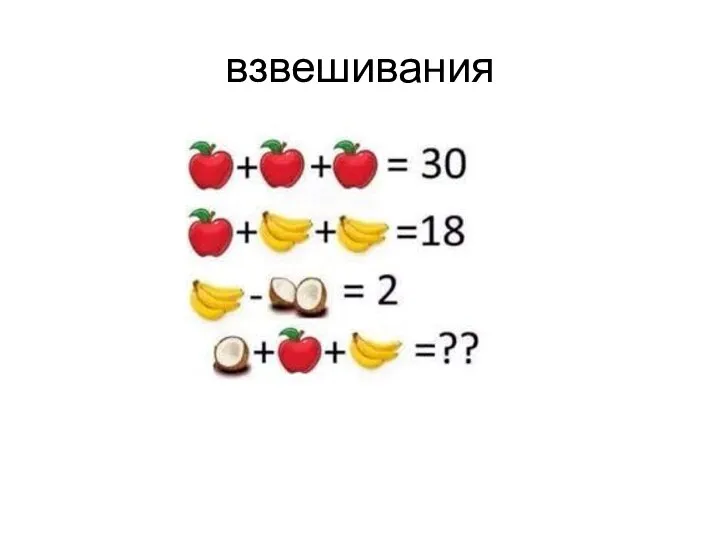 Взвешивания. Домашнее задание 1 класс
Взвешивания. Домашнее задание 1 класс Задачи на кратное сравнение
Задачи на кратное сравнение Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов Функция y = хх и её график
Функция y = хх и её график Понятия много и один. Число и цифра 1
Понятия много и один. Число и цифра 1