consideră:
P – o problemă de calcul;
D – set de date de intrare exacte;
D* - set de date de intrare uşor perturbate faţă de setul de date D;
P(D) – soluţia matematică exactă, obţinută lucrând cu datele exacte D;
P(D*) - soluţia matematică exactă, obţinută lucrând cu datele perturbate D*.
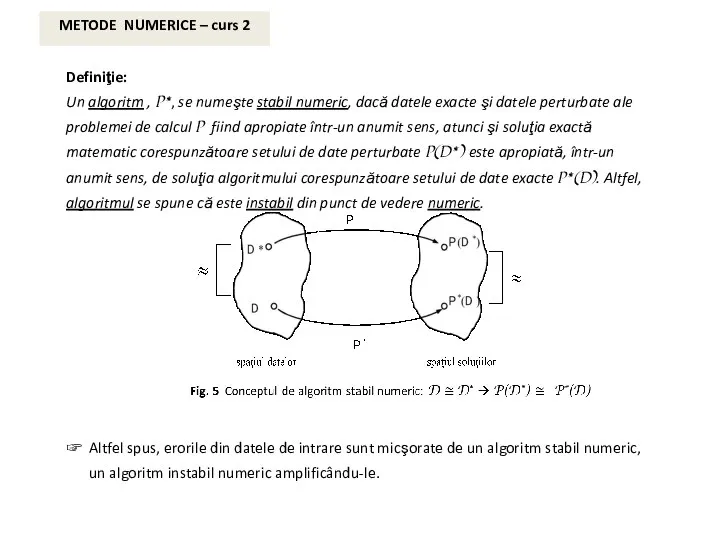
Definiţie:
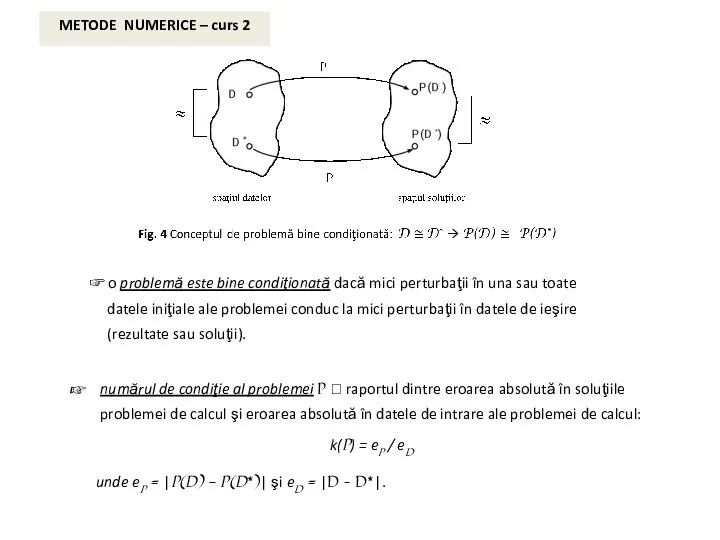
Problema de calcul, P, se spune că este bine condiţionată dacă datele exacte ale problemei, D, şi datele perturbate ale problemei, D*, fiind apropiate într-un anumit sens, atunci şi soluţia exactă matematic a problemei de calcul corespunzătoare datelor exacte, P(D) este apropiată, într-un anumit sens de soluţia exactă matenatic a problemei de calcul corespunzătoare datelor perturbate. Altfel, se spune că problema de calcul este prost (rău) condiţionată.
METODE NUMERICE – curs 2











 Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Операции над множествами
Операции над множествами Площадь трапеции
Площадь трапеции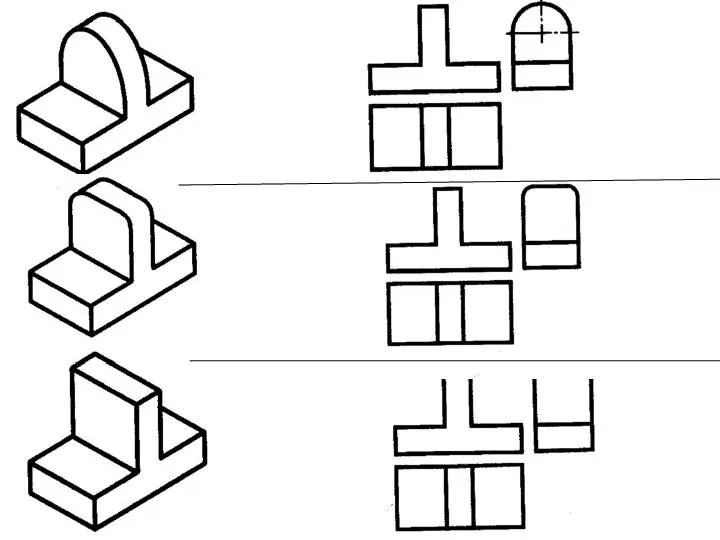 Проецирование на три взаимно перпендикулярные плоскости проекций
Проецирование на три взаимно перпендикулярные плоскости проекций Математика
Математика Вычислительная сложность алгоритма
Вычислительная сложность алгоритма Доли. 3 класс
Доли. 3 класс Задачі на проценти
Задачі на проценти 08.09
08.09 Разряды и классы чисел
Разряды и классы чисел тригонометрические неравенства (1)
тригонометрические неравенства (1)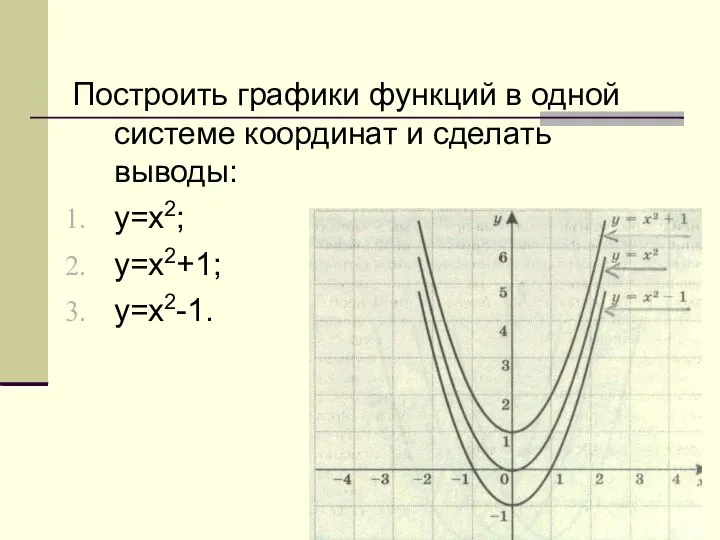 Графики функций в одной системе координат
Графики функций в одной системе координат Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс ЕГЭ. Математика. Задание № 5. Решение простейших тригонометрических уравнений
ЕГЭ. Математика. Задание № 5. Решение простейших тригонометрических уравнений Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Ukazania_k_vypolneniyu_raboty_5
Ukazania_k_vypolneniyu_raboty_5 Сложение и вычитание смешанных чисел. Подготовка к контрольной работе
Сложение и вычитание смешанных чисел. Подготовка к контрольной работе Площадь треугольника
Площадь треугольника Начала теории вероятности
Начала теории вероятности Положительные и отрицательные числа (6 класс)
Положительные и отрицательные числа (6 класс) Решение задач
Решение задач Презентация на тему Многообразие и происхождение культурных растений
Презентация на тему Многообразие и происхождение культурных растений  Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Виды углов.Измерение углов
Виды углов.Измерение углов Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Решение задач
Решение задач Наименьшее значение выражения
Наименьшее значение выражения