Содержание
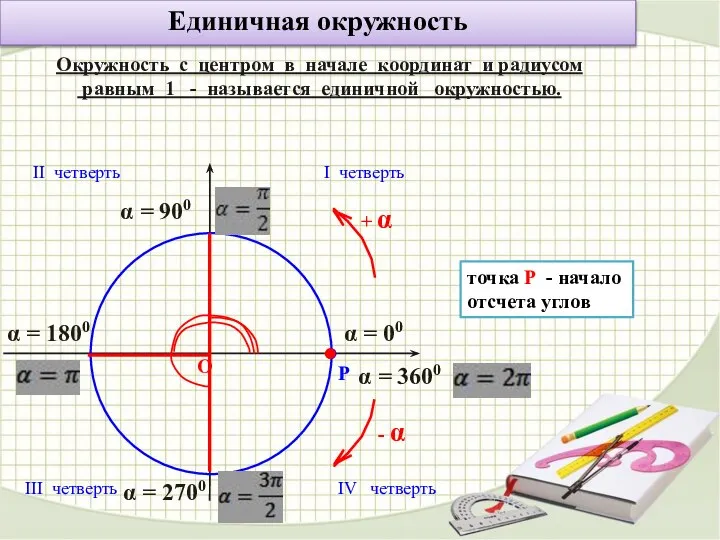
- 2. Единичная окружность Окружность с центром в начале координат и радиусом равным 1 - называется единичной окружностью.
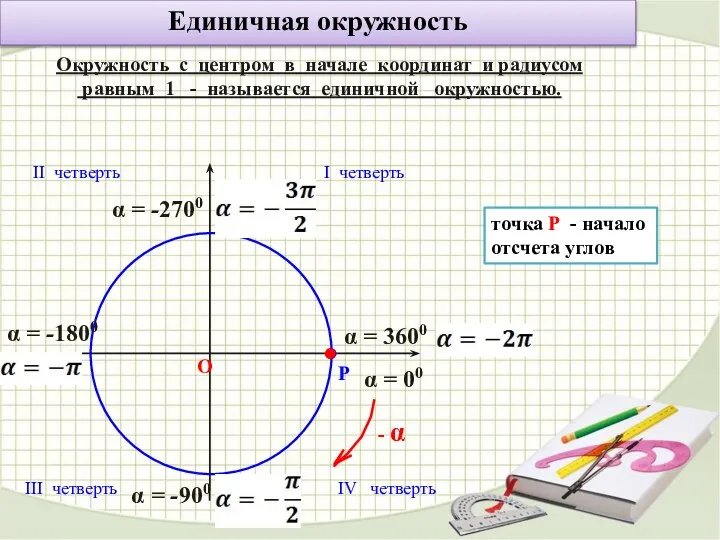
- 3. Единичная окружность Окружность с центром в начале координат и радиусом равным 1 - называется единичной окружностью.
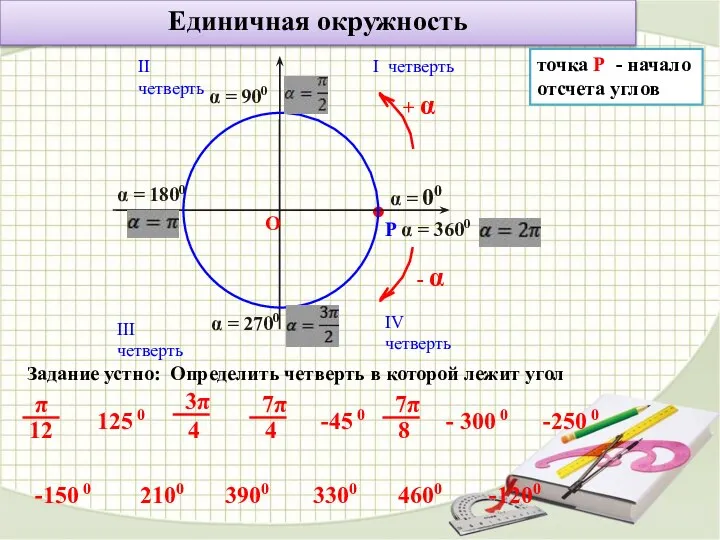
- 4. Единичная окружность точка Р - начало отсчета углов Задание устно: Определить четверть в которой лежит угол
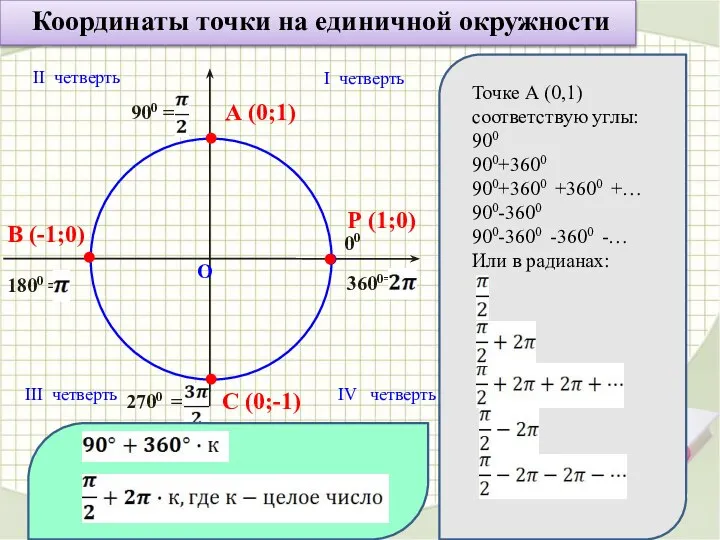
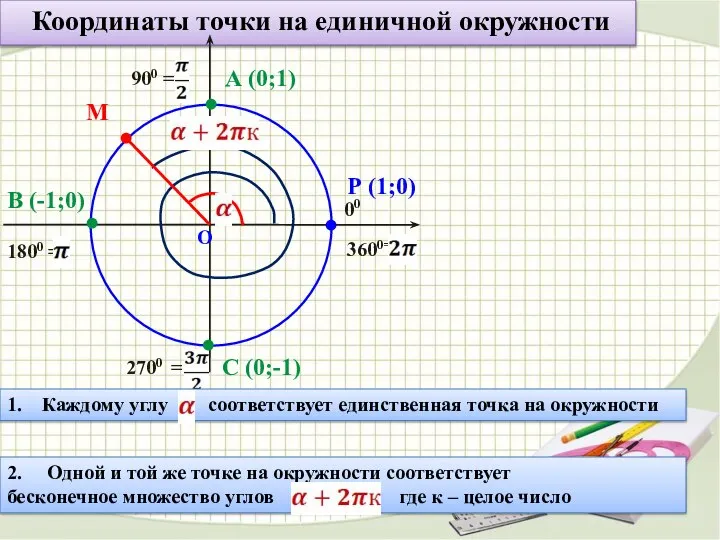
- 5. Координаты точки на единичной окружности О Р (1;0) I четверть II четверть III четверть IV четверть
- 6. Координаты точки на единичной окружности О Р (1;0) 00 900 = 1800 = 2700 = 3600=
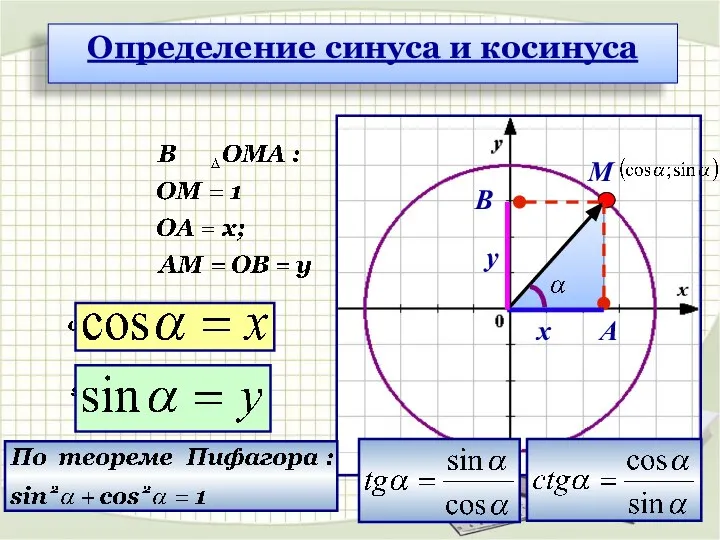
- 7. x y A B M Определение синуса и косинуса
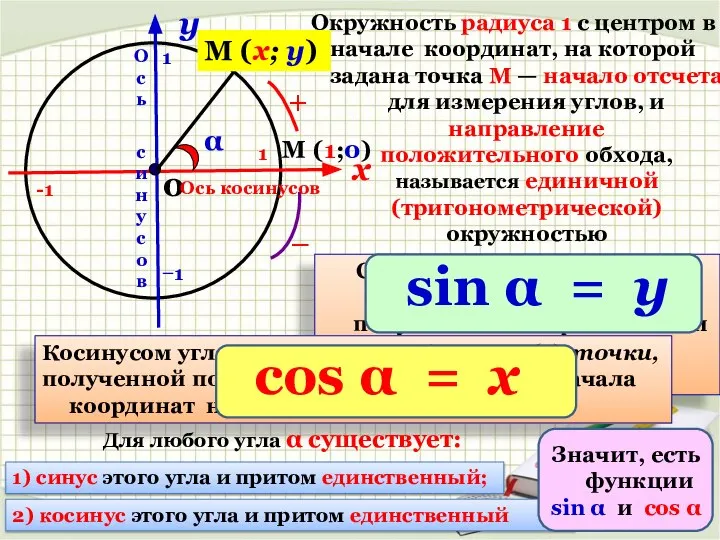
- 8. х у 0 Окружность радиуса 1 с центром в начале координат, на которой задана точка М
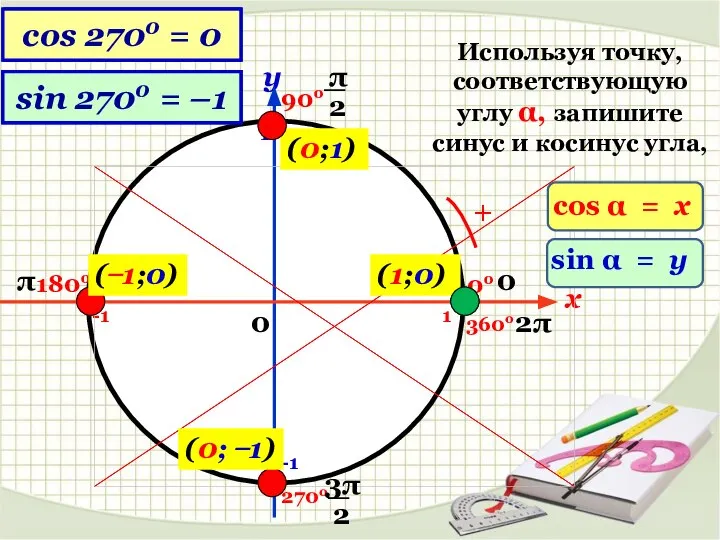
- 9. x y 1 -1 1 -1 0 (1;0) (0;1) ( ̶ 1;0) (0; ̶ 1) Используя
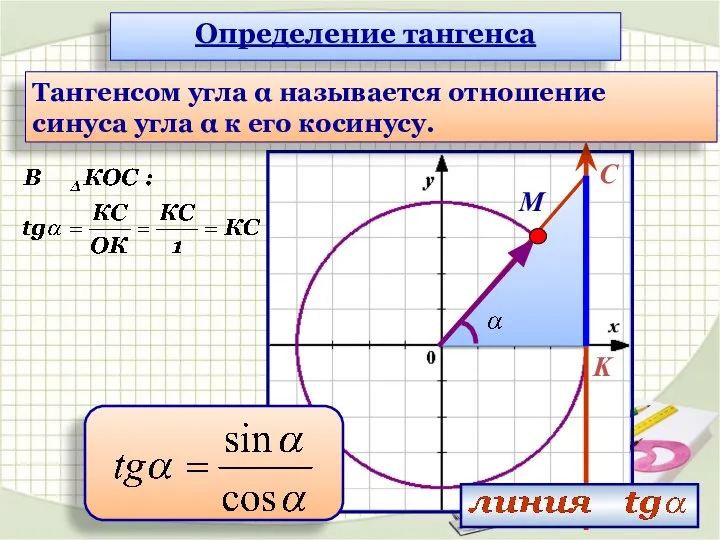
- 10. M C K Определение тангенса Тангенсом угла α называется отношение синуса угла α к его косинусу.
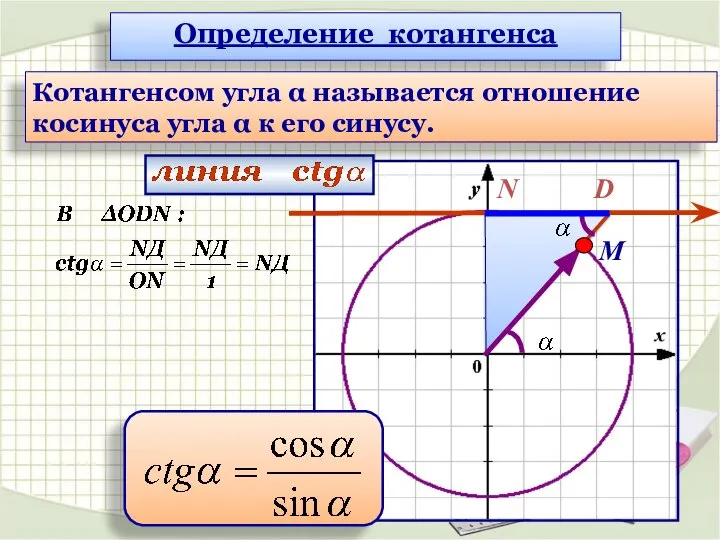
- 11. M D N Определение котангенса Котангенсом угла α называется отношение косинуса угла α к его синусу.
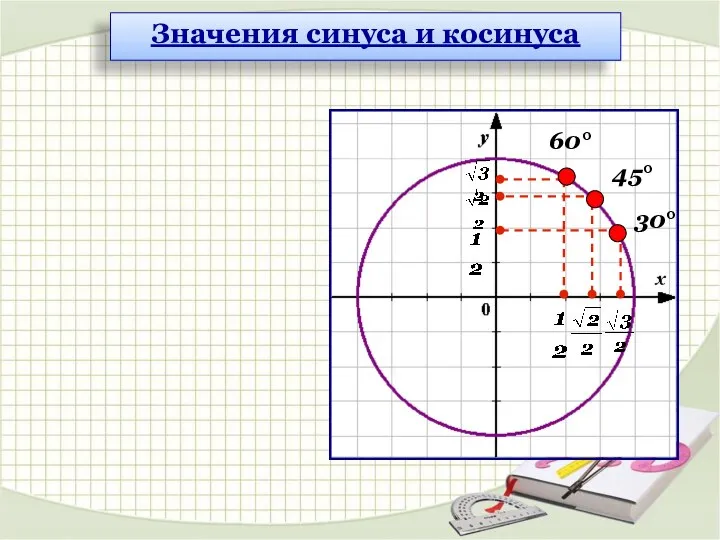
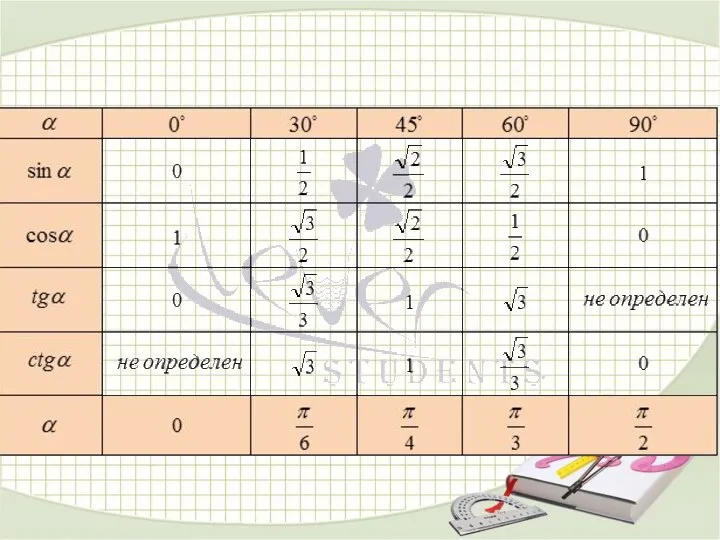
- 12. 30° 45° 60° Значения синуса и косинуса
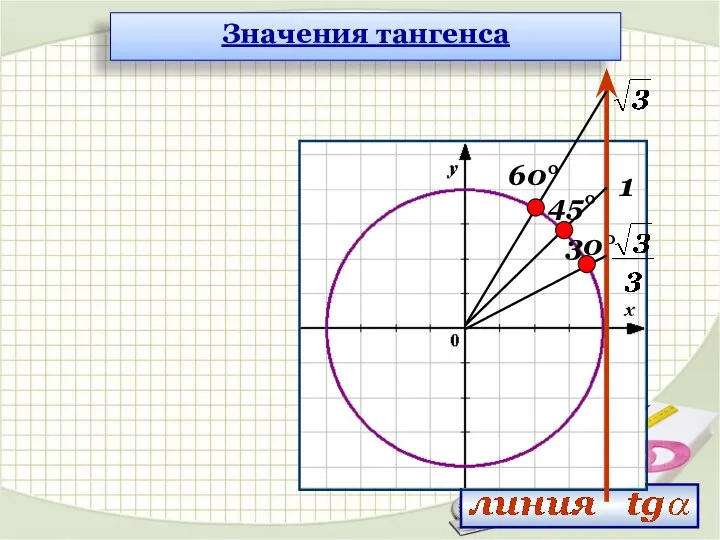
- 14. 30° 45° 60° 1 Значения тангенса
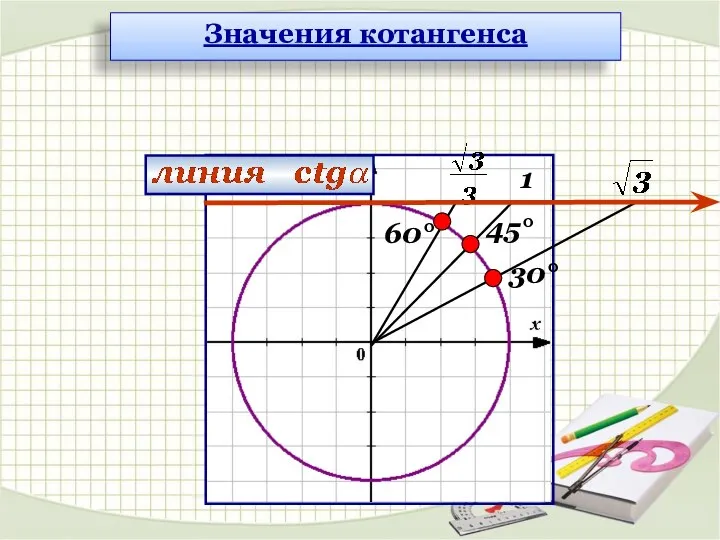
- 15. 30° 45° 60° 1 Значения котангенса
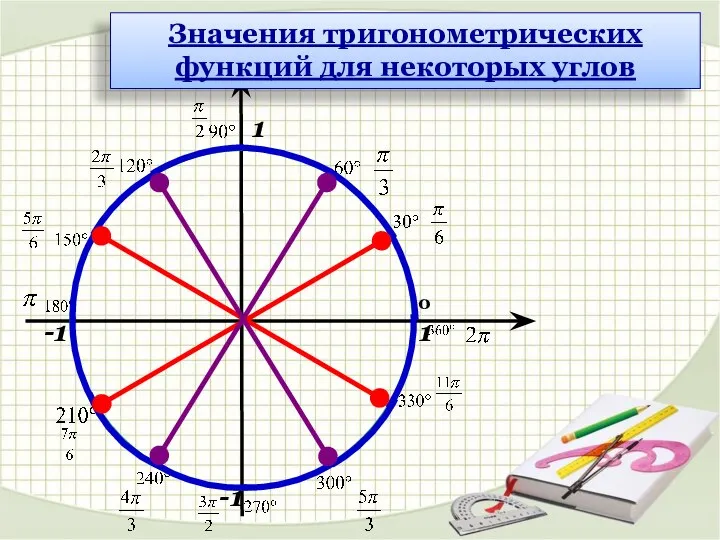
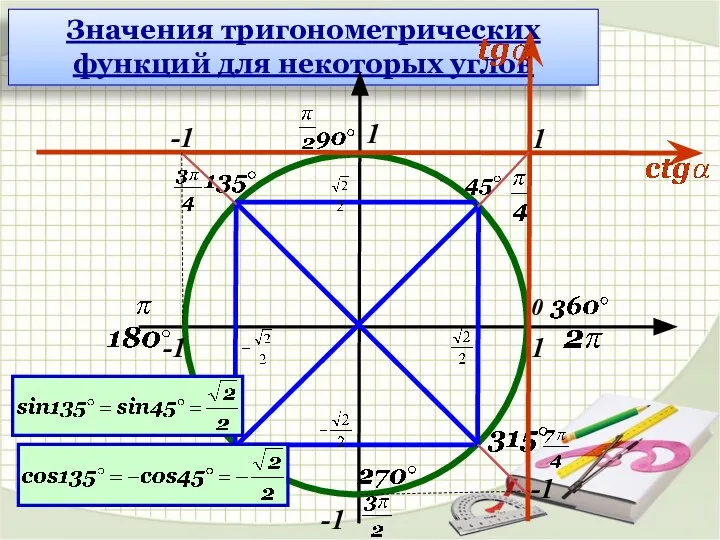
- 16. 1 1 -1 -1 0 Значения тригонометрических функций для некоторых углов
- 17. Значения тригонометрических функций для некоторых углов 1 1 -1 -1 0
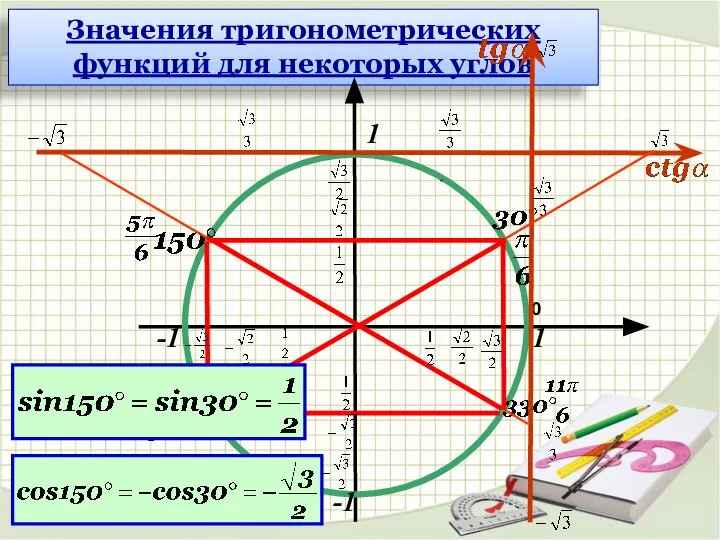
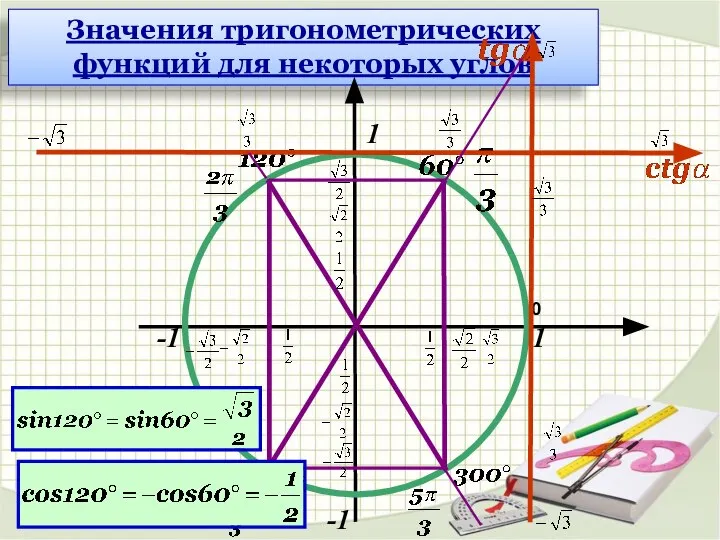
- 18. Значения тригонометрических функций для некоторых углов 1 1 -1 -1 0
- 19. Значения тригонометрических функций для некоторых углов 1 1 -1 -1 0 1 -1 -1
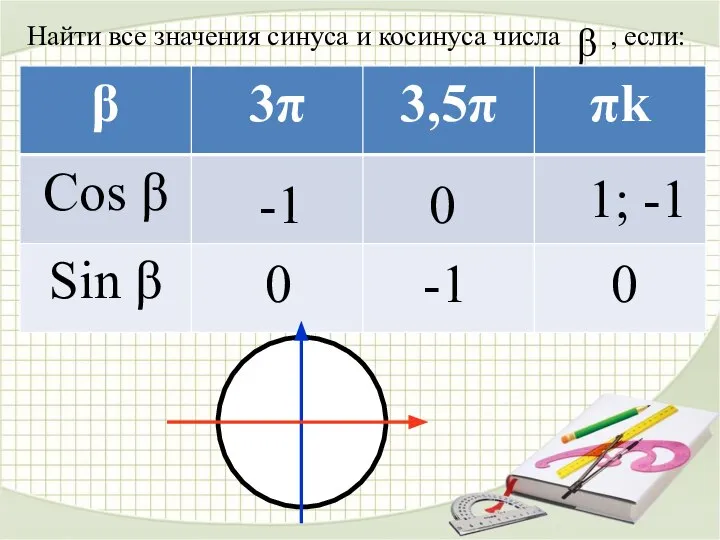
- 21. Найти все значения синуса и косинуса числа , если: β -1 -1 1; -1 0 0
- 23. Скачать презентацию

 Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1) Аттестационная работа. Элективный кружок, как элемент проектной деятельности
Аттестационная работа. Элективный кружок, как элемент проектной деятельности Углы, образованные хордами, секущими, касательными. Свойство отрезков хорд и касательных
Углы, образованные хордами, секущими, касательными. Свойство отрезков хорд и касательных Параллельность прямой и плоскости
Параллельность прямой и плоскости Тела вращения. Цилиндр
Тела вращения. Цилиндр Функция. Свойства функции. График функции
Функция. Свойства функции. График функции Свойства корня п- ой степени
Свойства корня п- ой степени Производные тригонометрических функций. 10 класс
Производные тригонометрических функций. 10 класс Параллелограмм. Свойства параллельных прямых
Параллелограмм. Свойства параллельных прямых Презентация на тему Игра по теме "Степень и ее свойства"
Презентация на тему Игра по теме "Степень и ее свойства"  Решение тригонометрических уравнений
Решение тригонометрических уравнений Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 16
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 16 Парная регрессия и корреляция. Тема 2
Парная регрессия и корреляция. Тема 2 Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Рюкзак. Восстановление ответа
Рюкзак. Восстановление ответа Римские цифры
Римские цифры Свойство противоположных сторон четырехугольника
Свойство противоположных сторон четырехугольника Пирамида
Пирамида С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике Элементы теории обобщенных функций
Элементы теории обобщенных функций Соответствия. Отношения и функции
Соответствия. Отношения и функции Практика. Дискретная математика
Практика. Дискретная математика Деление окружности на равные части
Деление окружности на равные части Наглядная геометрия. Деление области с помощью линий1 класс
Наглядная геометрия. Деление области с помощью линий1 класс Преобразование функций и действия над ними
Преобразование функций и действия над ними Математические основы информатики. Элементы комбинаторики. (Тема 1)
Математические основы информатики. Элементы комбинаторики. (Тема 1) Полное исследование функций и построение их графиков
Полное исследование функций и построение их графиков Нелинейная парная регрессия
Нелинейная парная регрессия