Содержание
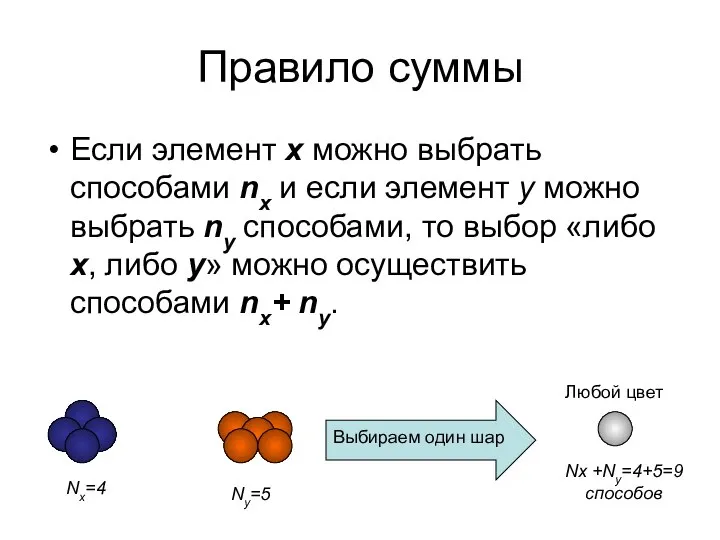
- 3. Правило суммы Если элемент x можно выбрать способами nx и если элемент y можно выбрать ny
- 4. Пример 1 В коробке 10 тетрадей в клетку и 5 тетрадей в линию. Сколькими способами можно
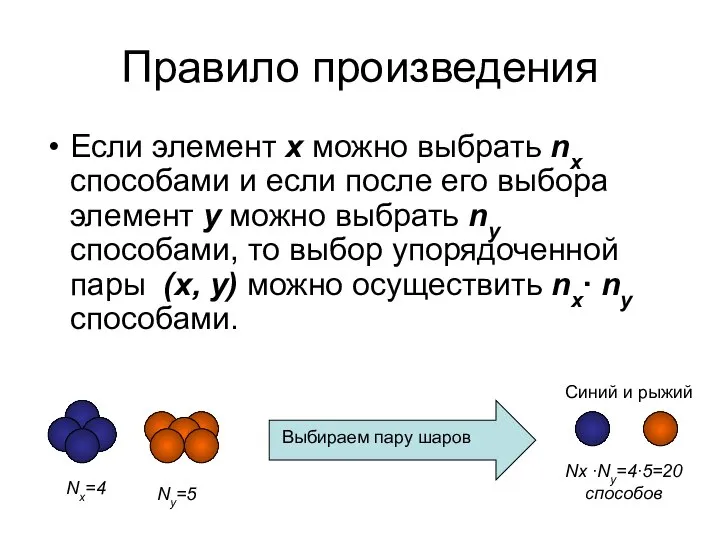
- 5. Правило произведения Если элемент x можно выбрать nx способами и если после его выбора элемент y
- 6. Пример 2 В магазине "Все для чая'' есть 5 разных чашек и 3 разных блюдца. Сколькими
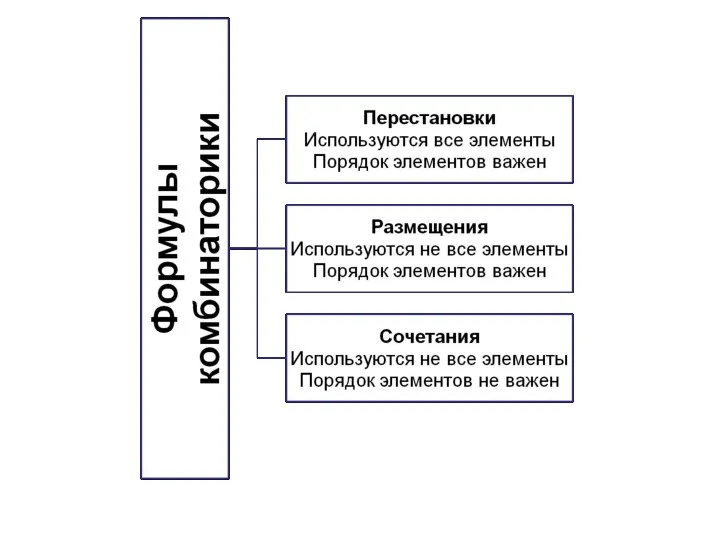
- 7. Перестановки
- 8. Перестановки без повторений Перестановками без повторений из n различных элементов называются все возможные последовательности этих n
- 9. Перестановки без повторений 6 различных перестановок
- 10. Пример 3 Сколько различных гирлянд можно сделать из 10 светодиодов разного цвета?
- 11. Перестановки с повторениями Перестановки с повторением из n элементов k типов число элементов 1-го типа n1;
- 12. Перестановки с повторениями n1=2 n2=1 n=n1+n2=2+1=3 3 различные перестановки
- 13. Пример 4 Дворовая футбольная команда выбирает капитана и его заместителя. Сколькими способами это можно сделать, если
- 14. Пример 5 Сколько различных гирлянд можно сделать, если у нас 5 красных, 7 синих и 4
- 15. Размещения (выборки)
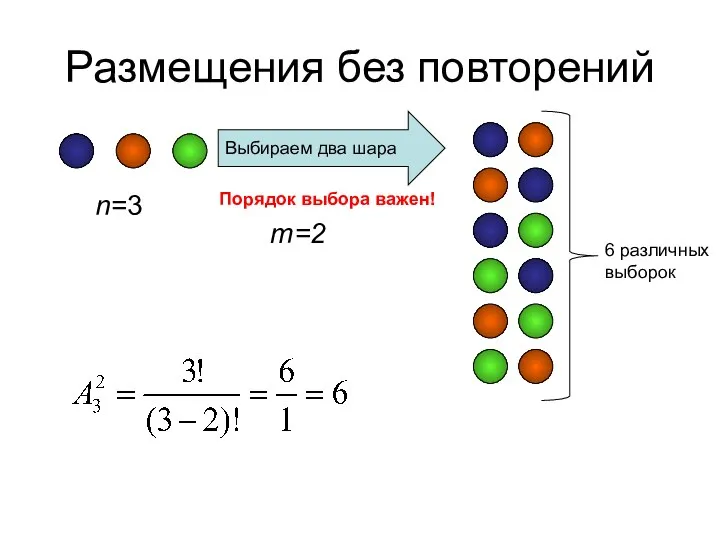
- 16. Размещения без повторений Размещениями без повторений из n различных элементов по m элементов называются все такие
- 17. Размещения без повторений n=3 Выбираем два шара m=2 Порядок выбора важен! 6 различных выборок
- 18. Пример 6 Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные
- 19. Пример 7 Из группы в 15 человек выбирается 4 участника эстафеты 800+400+200+100. Сколькими способами можно расставить
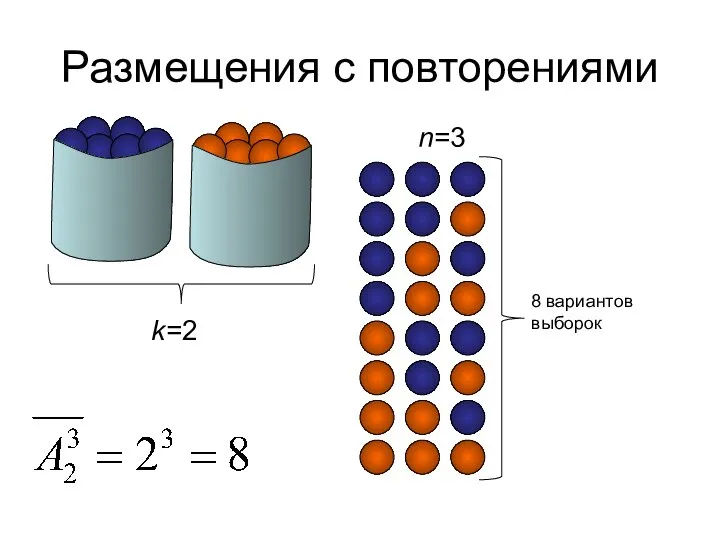
- 20. Размещения с повторениями Размещения с повторениями из элементов k типов по m элементов (k и m
- 21. Размещения с повторениями k=2 n=3 8 вариантов выборок
- 22. Пример 8 Назовем натуральное число "симпатичным", если в его записи встречаются только нечетные цифры. Сколько существует
- 23. Сочетания
- 24. Сочетания без повторений Сочетаниями без повторений из n различных элементов по m элементов называются все такие
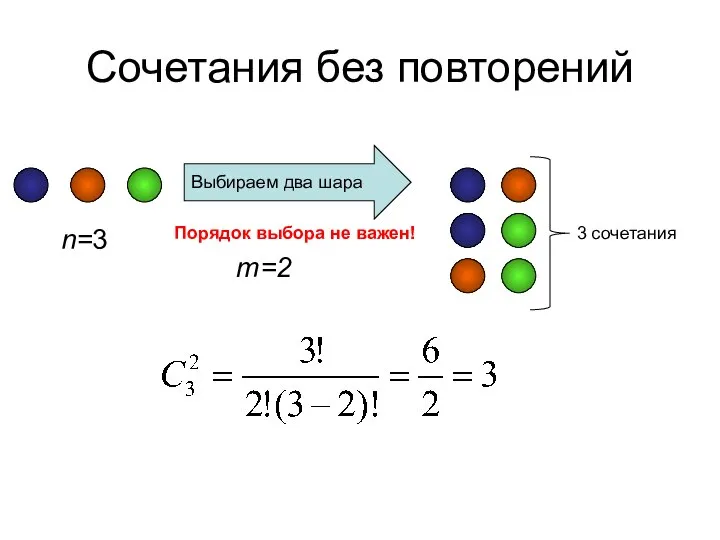
- 25. Сочетания без повторений n=3 Выбираем два шара m=2 Порядок выбора не важен! 3 сочетания
- 26. Пример 9 Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
- 27. Сочетания с повторениями Сочетаниями с повторениями из элементов k типов по m элементов (m и k
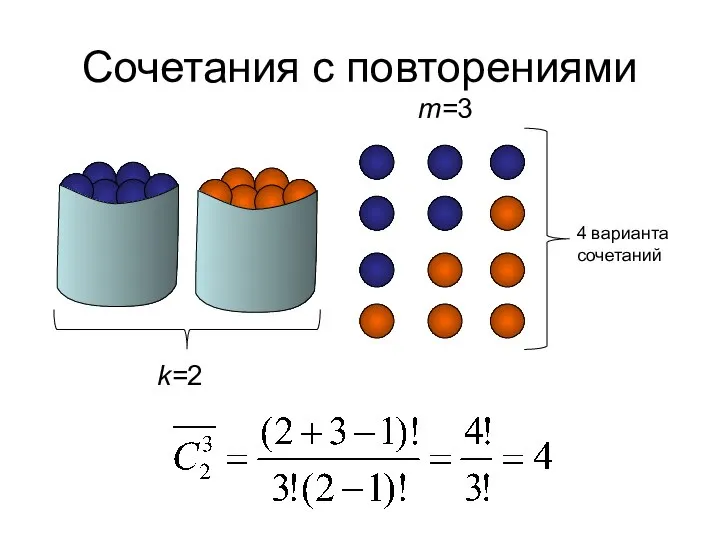
- 28. Сочетания с повторениями k=2 m=3 4 варианта сочетаний
- 29. Пример 10 В вазе стоят 10 красных и 4 розовых гвоздики. Все цветы на внешний вид
- 31. Один выбор (анализ) элементов или несколько? Если один, то см. п.3 Каким союзом варианты выбора (анализа)
- 32. Пример 11 Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний
- 33. Пример 12 У людоеда в подвале томятся 25 пленников. а) Сколькими способами он может выбрать трех
- 34. Пример 13 Волонтеры разделились на две равные группы для розыска заблудившегося ребенка. Среди них только 4
- 35. Пример 14 Сколько существует натуральных чисел, меньших 25610, таких, что в записи каждого числа в двоичной
- 37. Скачать презентацию



























 действительные числа
действительные числа Последние цифры степеней
Последние цифры степеней Черчение геометрических фигур не отрывая карандаш от бумаги
Черчение геометрических фигур не отрывая карандаш от бумаги Животные в мире математики
Животные в мире математики Пирамида. Творческая групповая работа 11класс
Пирамида. Творческая групповая работа 11класс Криволинейная трапеция
Криволинейная трапеция Задачи на готовых чертежах по теме Подобие
Задачи на готовых чертежах по теме Подобие Случаи сложения вида +5
Случаи сложения вида +5 بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی
بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی Умножение на двузначные и трёхзначные числа
Умножение на двузначные и трёхзначные числа Дифференциальные уравнения в частных производных. Лекция1
Дифференциальные уравнения в частных производных. Лекция1 Определение.Модуль числа а
Определение.Модуль числа а Фронтовой теугольник
Фронтовой теугольник Лабораторная работа № 1
Лабораторная работа № 1 Функция у = √х, ее свойства и график
Функция у = √х, ее свойства и график Предметы геометрической формы. Логические задания
Предметы геометрической формы. Логические задания Преобразования графиков
Преобразования графиков Вычитание дроби из целого числа (урок 116)
Вычитание дроби из целого числа (урок 116) Объемы многогранников
Объемы многогранников Теорема Пифагора
Теорема Пифагора Математика и театр
Математика и театр Мир функций и графиков. Урок - аукцион
Мир функций и графиков. Урок - аукцион Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента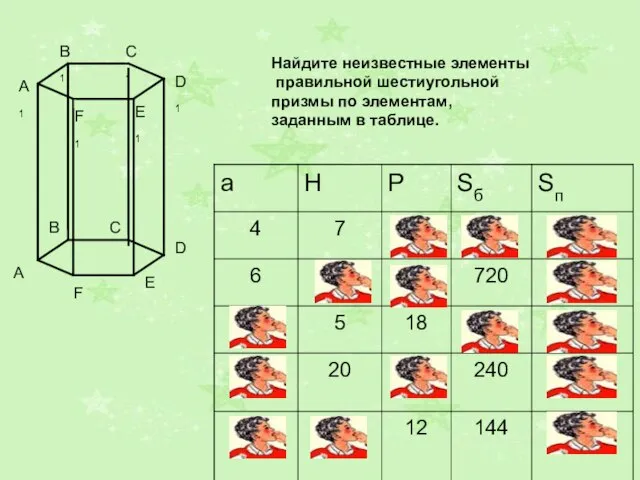 Задачи по призме
Задачи по призме Умножение дробей. Анаграммы
Умножение дробей. Анаграммы Движение, 9 класс
Движение, 9 класс Таблица сложения
Таблица сложения Призма. Построение сечений призмы плоскостями
Призма. Построение сечений призмы плоскостями