Содержание
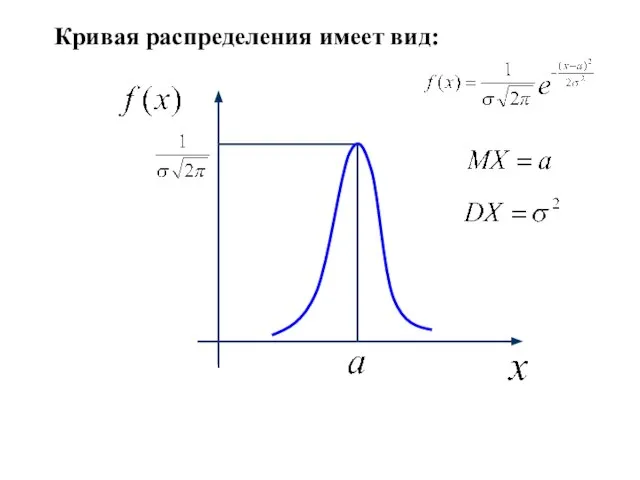
- 2. Кривая распределения имеет вид:
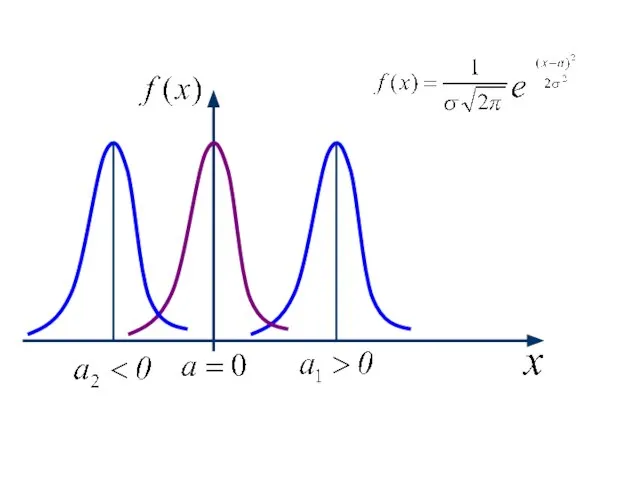
- 3. Если изменять параметр a , кривая распределения будет смещаться вдоль оси абсцисс, не изменяя при этом
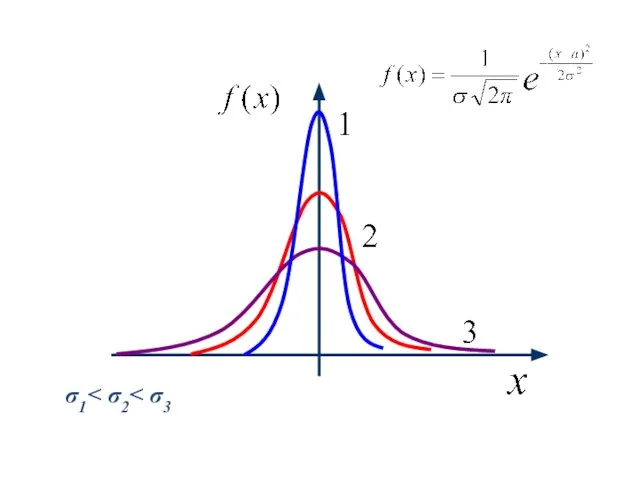
- 5. Параметр σ характеризует форму кривой распределения. При его увеличении кривая распределения становится более плоской, и наоборот.
- 6. σ1
- 7. То, что случайная величина Х распределена по нормальному закону с параметрами a, σ>0 , обозначается
- 10. Интеграл аналитически не вычисляется!
- 11. 1 способ (при вычислении в Excel) функция нормального Распределения, для вычисления Которой используется функция НОРМРАСП(x;a;σ;1)
- 12. 1 способ (при вычислении в Excel) Например, если Х имеет нормальное распределение со средним a=4 и
- 13. Например, если Х имеет нормальное распределение со средним a=4 и среднеквадратичным отклонением σ=2, то для вычисления
- 15. Например, если Х имеет нормальное распределение со средним a=4 и среднеквадратичным отклонением σ=2, то для вычисления
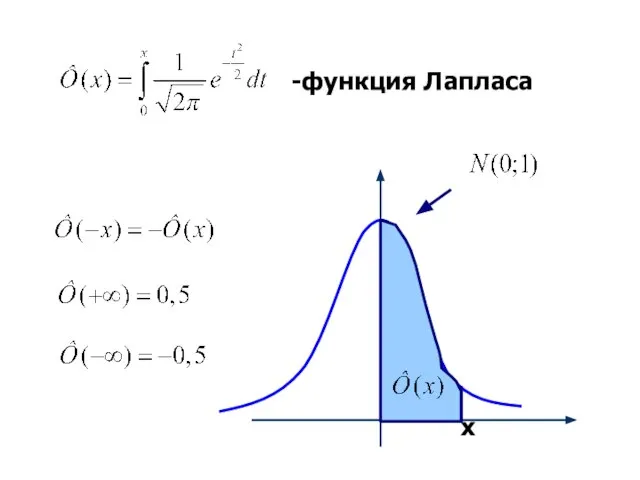
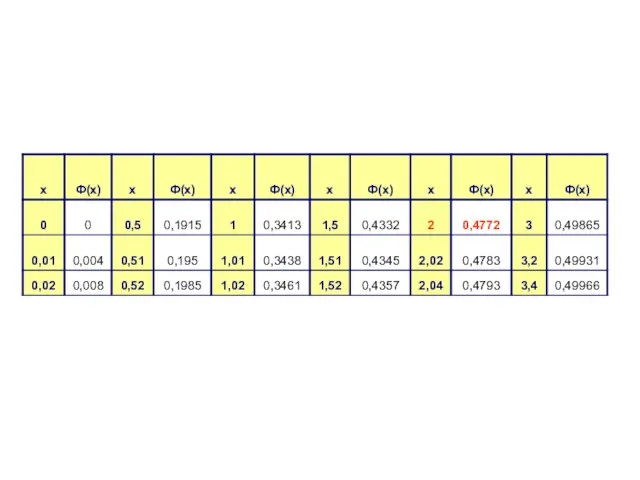
- 16. 2 способ (при вычислении вручную) Ф(x) – табличная функция Лапласа
- 17. -функция Лапласа х
- 21. Пусть случайная величина Х - рост наугад выбранного студента подчиняется нормальному распределению с параметром a=174 см.
- 22. РЕШЕНИЕ. В Excel пишем =НОРМРАСП(190;174;6;1) Вручную Находим в таблице Лапласа
- 23. РЕШЕНИЕ. В Excel пишем =1-НОРМРАСП(180;174;6;1) Вручную
- 24. В Excel пишем =НОРМРАСП(190;174;6;1)- НОРМРАСП(160;174;6;1) Вручную Находим в таблице Лапласа
- 25. Пусть Х - нормально распределенная случайная величина с параметрами a, σ. Тогда ПРАВИЛО ТРЕХ СИГМ
- 26. Действительно,
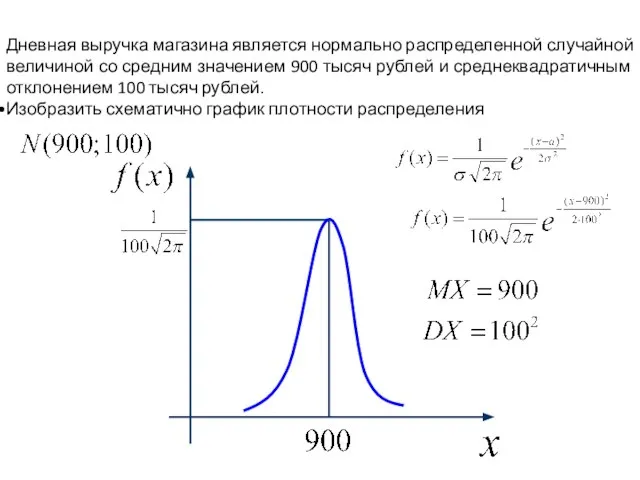
- 27. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 900 тысяч рублей и среднеквадратичным
- 28. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 900 тысяч рублей и среднеквадратичным
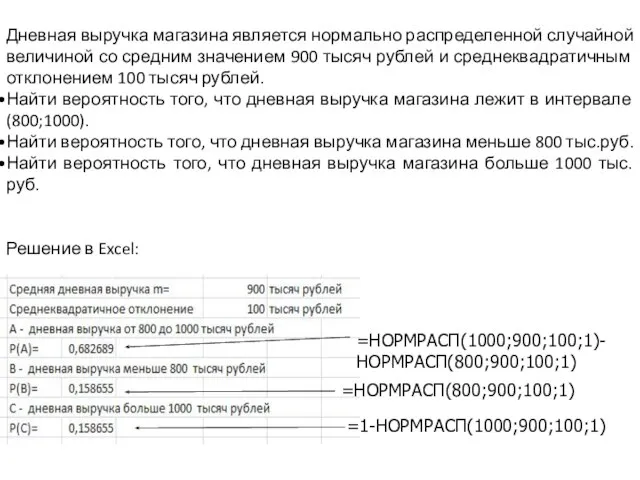
- 29. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 900 тысяч рублей и среднеквадратичным
- 30. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 900 тысяч рублей и среднеквадратичным
- 31. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 900 тысяч рублей и среднеквадратичным
- 32. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 900 тысяч рублей и среднеквадратичным
- 34. Скачать презентацию



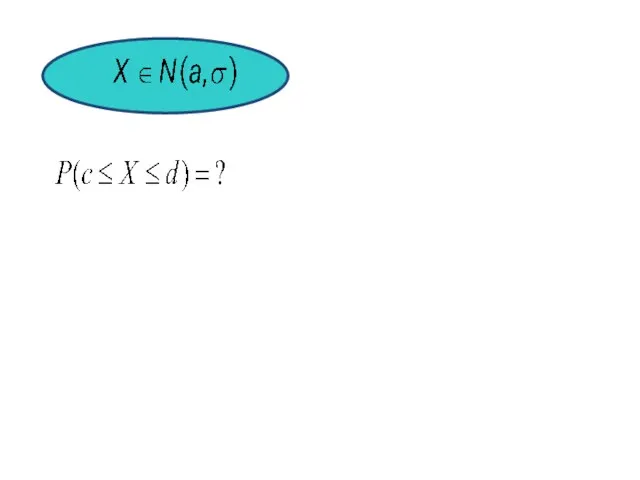
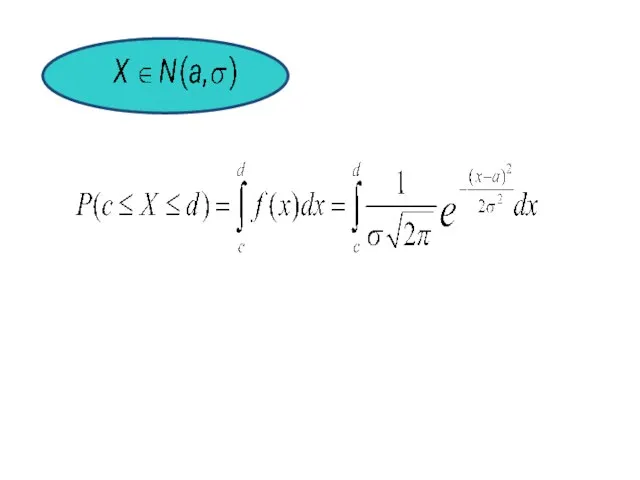




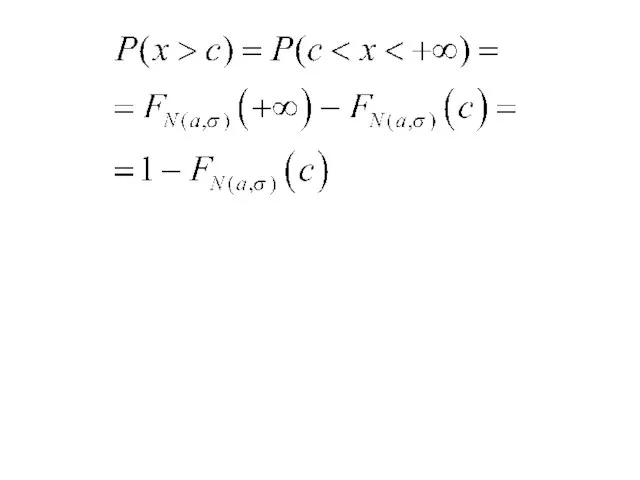


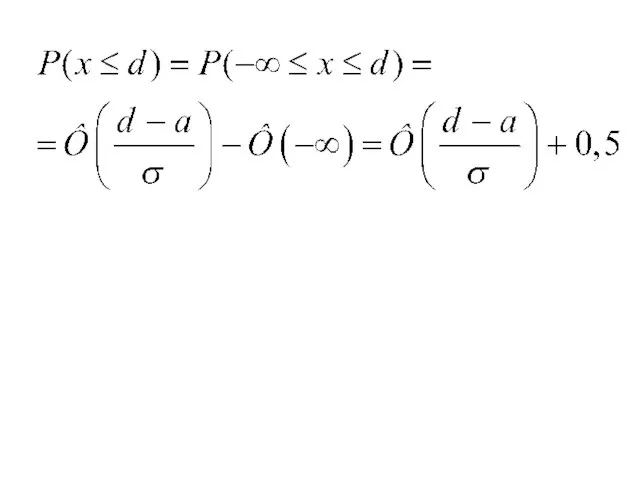
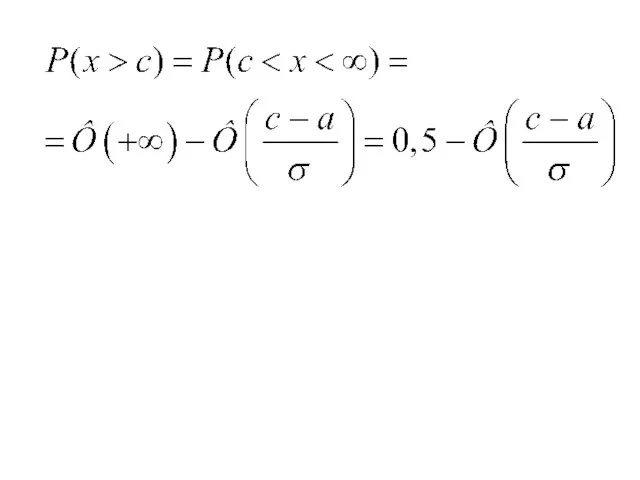










 Число 10
Число 10 Сумма углов в треугольнике
Сумма углов в треугольнике Перестановочные тесты и бутстреп анализ
Перестановочные тесты и бутстреп анализ Старинные меры длины на Руси
Старинные меры длины на Руси Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Устный счёт для дошкольников
Устный счёт для дошкольников Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности
Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности Графическое решение уравнений
Графическое решение уравнений Презентация на тему Типы параллелепипеда
Презентация на тему Типы параллелепипеда  Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Трапеция. Задачи по готовым чертежам
Трапеция. Задачи по готовым чертежам Морфизмы алгебр
Морфизмы алгебр Дополни до 10
Дополни до 10 Решение уравнений (2 класс)
Решение уравнений (2 класс) Задачи. вариант 3
Задачи. вариант 3 Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Стереометрические задачи повышенной сложности
Стереометрические задачи повышенной сложности Векторы
Векторы Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Взаимное пересечение двух поверхностей. Лекция 9
Взаимное пересечение двух поверхностей. Лекция 9 Начальные понятия геометрии
Начальные понятия геометрии Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни
Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни Преобразование обыкновенных дробей в десятичные
Преобразование обыкновенных дробей в десятичные Числа 1,2. Цифры 1,2
Числа 1,2. Цифры 1,2 Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Презентация на тему Арифметические действия с десятичными дробями
Презентация на тему Арифметические действия с десятичными дробями  Деление дробей
Деление дробей