Содержание
- 2. Будем обозначать случайные величины Х, а их возможные значения х. Например, пусть Х - число очков,
- 3. Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е. все возможные значения можно пронумеровать
- 4. Дискретная случайная величина полностью определяется своим рядом распределения. Ряд распределения представляет собой таблицу, в которой указаны
- 6. ПРИМЕР. Игральный кубик бросается 1 раз. Пусть случайная величина Х - число выпавших очков. Составим для
- 7. Многоугольник распределения – ломаная, которая соединяет точки, абсциссы которых содержит первая строка ряда распределения (значения случайной
- 8. ПРИМЕР. В лотерее 100 билетов, из которых 2 выигрышных по 110 руб. и 10 выигрышных по
- 9. ПРИМЕР. Студент в сессию должен сдать 3 экзамена, причем известно, что положительную оценку он может получить
- 10. ПРИМЕР. Пусть Х – число мальчиков в случайно взятой семье с тремя детьми. Построить ряд распределения
- 12. Скачать презентацию









 Кратные интегралы
Кратные интегралы Прямоугольный треугольник
Прямоугольный треугольник Окружность и круг
Окружность и круг Сравнение отрезков и углов
Сравнение отрезков и углов Сумма углов треугольника
Сумма углов треугольника Закрепление пройденного материала. 1 класс
Закрепление пройденного материала. 1 класс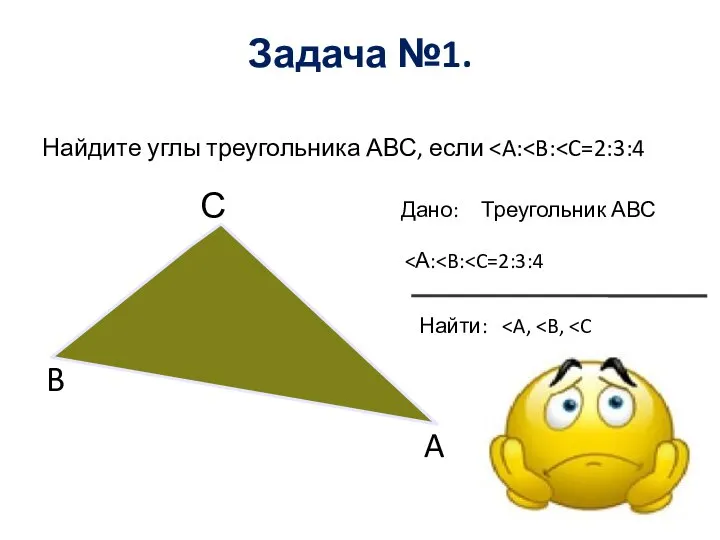 Решение задач по геометрии
Решение задач по геометрии Тригонометрические функции двойного угла
Тригонометрические функции двойного угла Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников окружность — повторение
окружность — повторение Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Геометрический тренинг
Геометрический тренинг Понятие функции
Понятие функции Разложение суммы тригонометрических функций в произведение и наоборот
Разложение суммы тригонометрических функций в произведение и наоборот Математический КВН
Математический КВН Построение графиков функций
Построение графиков функций Правильные многогранники в представлении пяти стихий
Правильные многогранники в представлении пяти стихий Подготовка к ЕГЭ 2013 год. В9. Тема: Расстояние в пространстве
Подготовка к ЕГЭ 2013 год. В9. Тема: Расстояние в пространстве Презентация на тему Параллелограмм. Свойства параллелограмма
Презентация на тему Параллелограмм. Свойства параллелограмма  проект Артюшина
проект Артюшина Золотое сечение. Витрувий
Золотое сечение. Витрувий Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2) Формирование познавательных УУД у младших школьников при изучении геометрического материала
Формирование познавательных УУД у младших школьников при изучении геометрического материала Геометрия. Решение задач
Геометрия. Решение задач Многоугольник
Многоугольник Окружность. 7 класс
Окружность. 7 класс Площадь параллелограмма
Площадь параллелограмма Квадратные уравнения
Квадратные уравнения