Квадратные уравнения

КТО?
Кто внес вклад в изучение квадратных уравнений? Кто в истории математики
одним из первых начал их решать? Выполнив следующее задание, вы
узнаете ответ на этот вопрос.
Задание 1.
Решите неполные квадратные уравнения. Расположите корни по
Возрастанию и замените каждое число соответствующей буквой
( см. таблицу ниже ). Прочитайте ключевое слово.
1) х² – 49 = 0
2) 2 х²= 8
3) 3 х² – 2х = 0
4) 8 х² = 0
5) х² =4х
-7; 7
-2; 2
0; 2/3
0
0; 4
-7; -2; 0; 2/3; 2; 4; 7
Д И О Ф А Н Т

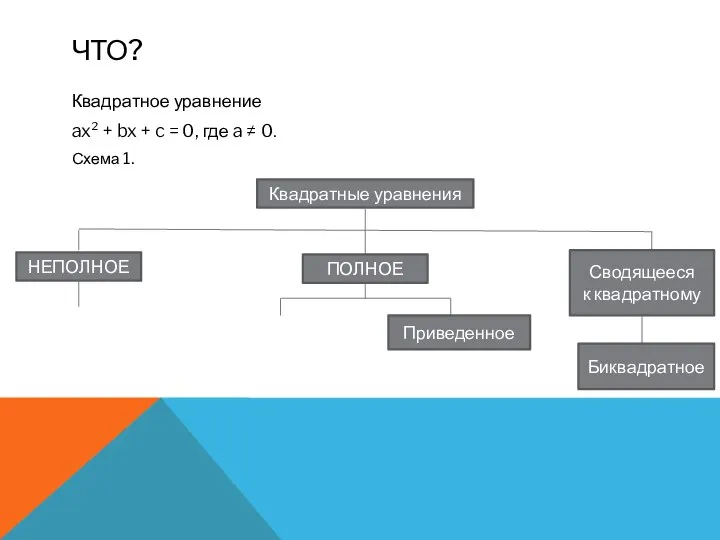
ЧТО?
Квадратное уравнение
ax² + bx + c = 0, где a ≠ 0.
Схема 1.
Квадратные уравнения
ПОЛНОЕ
НЕПОЛНОЕ
Сводящееся
к квадратному
Приведенное
Биквадратное

ЗАДАЧА №1.
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась.
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько, ты мне скажешь,
Обезьян там было в роще?
Решение.
Пусть в роще было х обезьян, тогда (х/8) ² + 12 = х. Решив полученное
квадратное уравнение, находим, что обезьян было 16 или 48.

ЗАДАЧА №2
Одна сторона прямоугольника на 5м больше другой. Площадь его равна 36м².
Вычислите стороны прямоугольника.
Решение.
Пусть меньшая сторона прямоугольника х м, тогда х(х + 5) = 36. Решив полученное
квадратное уравнение, получим: стороны прямоугольника 4 м и 9 м.

ЗАДАЧА № 3.
Определите, сколько секунд будет падать камень, брошенный вертикально с высоты 12 м.
Решение.
Из курса физики вам известна формула S = gt²/2.
После подстановки в формулу известных величин, мы получим квалратное
уравнение, корнем которого является t = √2.4 ≈ 1.5.
Ответ. 1,5 с.

ЗАДАЧА № 4.
Известно, что фасад здания в виде прямоугольника размером a × b
Производит наиболее приятное впечатление, когда отношение суммы его
длины и высоты к длине равно отношению длины к высоте. ( Такой выбор
размера фасада называется выбором по правилу «золотого деления» ).
Чему равна длина и высота фасада?
Решение.
Составим уравнение: ( a + b )/a = a/b,
1 + b/a = a/b.
Заменим a/b = t, тогда 1 + 1/t = t,
t² – t – 1

ЗАДАЧА № 5
ФИПИ ЕГЭ – 2015
31 декабря 2014 г. Антон взял в банке 1 млн рублей в кредит. Схема выплат
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на
определенное количество процентов), затем Антон переводит очередной
транш. Антон выплатил кредит за два транша, переводя в первый раз 510
тыс. рублей (Х), во второй раз 649 тыс. рублей (Y). Под какой процент банк
выдал кредит Антону?

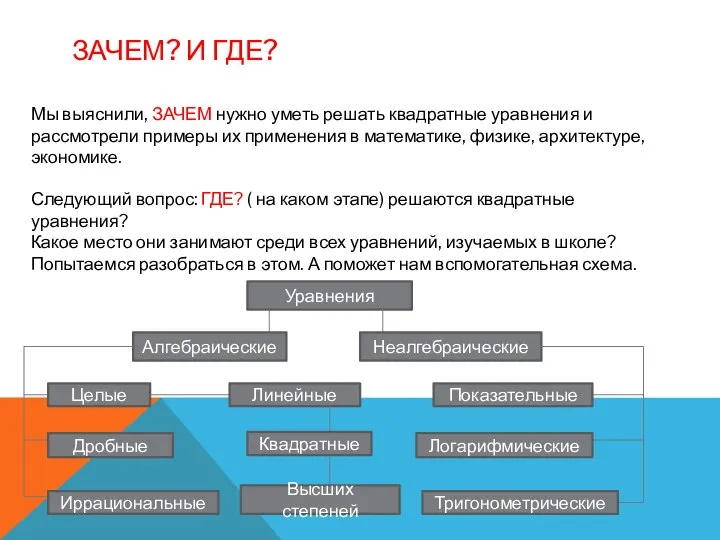
ЗАЧЕМ? И ГДЕ?
Мы выяснили, ЗАЧЕМ нужно уметь решать квадратные уравнения и
рассмотрели примеры их применения в математике, физике, архитектуре, экономике.
Следующий вопрос: ГДЕ? ( на каком этапе) решаются квадратные уравнения?
Какое место они занимают среди всех уравнений, изучаемых в школе?
Попытаемся разобраться в этом. А поможет нам вспомогательная схема.
Уравнения
Алгебраические
Неалгебраические
Целые
Дробные
Иррациональные
Линейные
Квадратные
Высших степеней
Показательные
Логарифмические
Тригонометрические

КАК?
Как же решать квадратные уравнения?
Помимо известных вам способов решения – по формулам корней и с
помощью теоремы. Обратной теореме Виета, есть и другие способы,
упрощающие решение некоторых уравнений. Рассмотрим два способа.

КОГДА?
Осталось ответить на вопрос: КОГДА?
Когда изучаются квадратные уравнения и будет ли эта тема иметь
Продолжение? Начинается изучение темы в курсе алгебры 8 класса, затем используется в 9 классе при изучении тем «Квадратичная функция» и «Квадратные неравенства», «Прогрессии», в 10-11 классах при решении неалгебраических уравнений.