Содержание
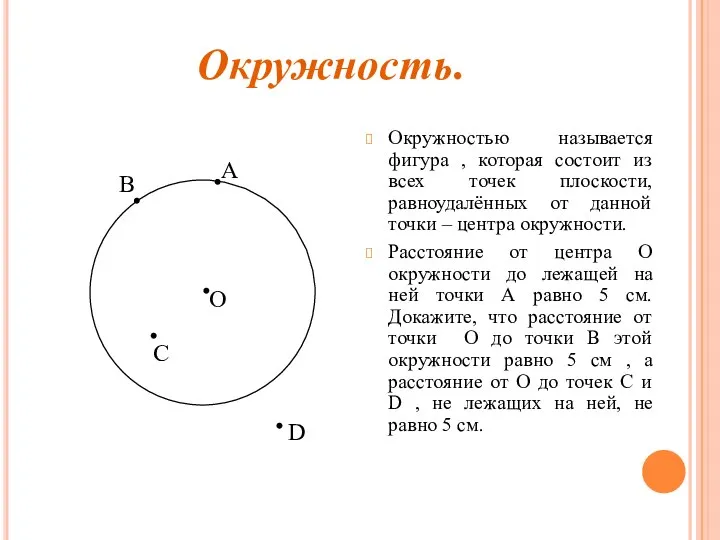
- 2. Окружностью называется фигура , которая состоит из всех точек плоскости, равноудалённых от данной точки – центра
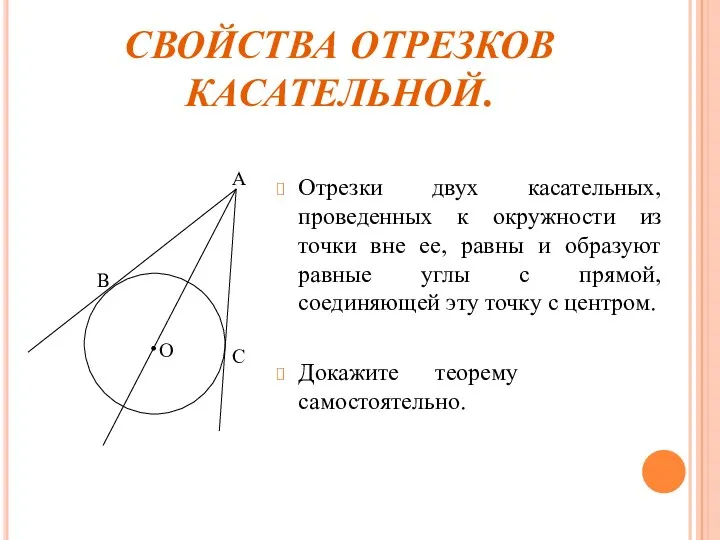
- 3. СВОЙСТВА ОТРЕЗКОВ КАСАТЕЛЬНОЙ. Отрезки двух касательных, проведенных к окружности из точки вне ее, равны и образуют
- 4. ЗАДАЧА. Из точки М к окружности с центром О и радиусом 8 см проведены касательные АМ
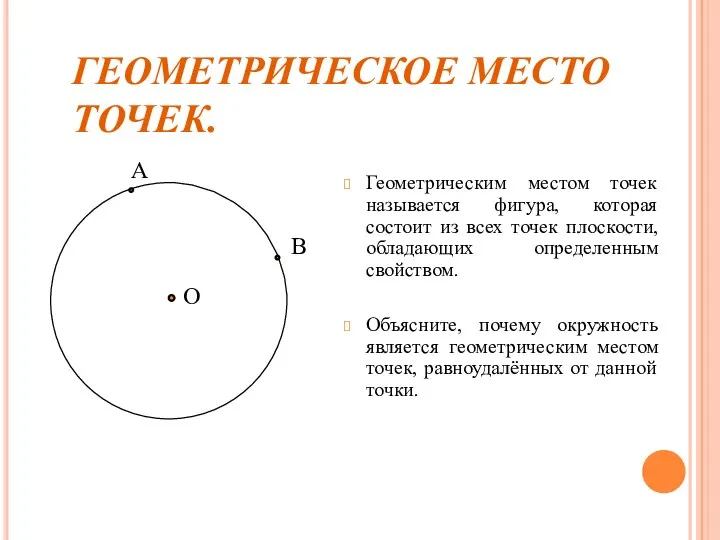
- 5. ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК. Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определенным
- 6. ТЕОРЕМА О ГЕОМЕТРИЧЕСКОМ МЕСТЕ ТОЧЕК. Геометрическое место точек, равноудалённых от двух данных точек, есть прямая, перпендикулярная
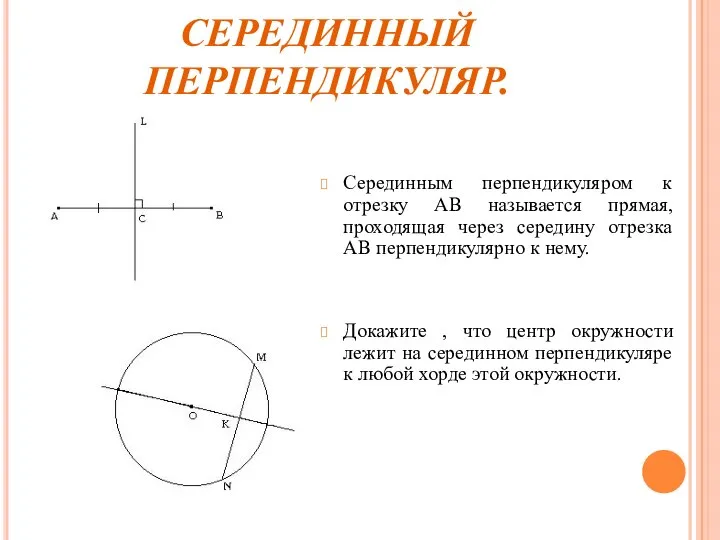
- 7. СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР. Серединным перпендикуляром к отрезку АВ называется прямая, проходящая через середину отрезка АВ перпендикулярно к
- 8. ОПИСАННАЯ ОКРУЖНОСТЬ. ТРЕУГОЛЬНИК, ВПИСАННЫЙ В ОКРУЖНОСТЬ. Окружность называется описанной около треугольника, если она проходит через все
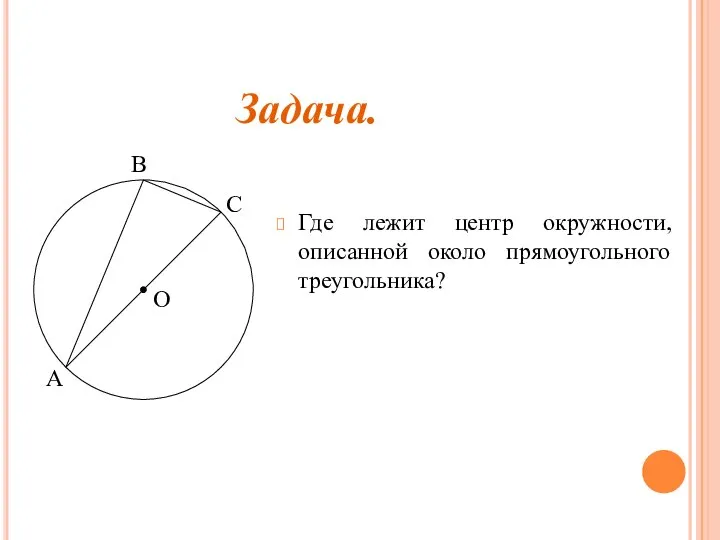
- 9. Где лежит центр окружности, описанной около прямоугольного треугольника? Задача.
- 10. ЗАДАЧА. Найдите радиус окружности, описанной около треугольника со сторонами 10, 12, и 10 см.
- 11. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности Общая
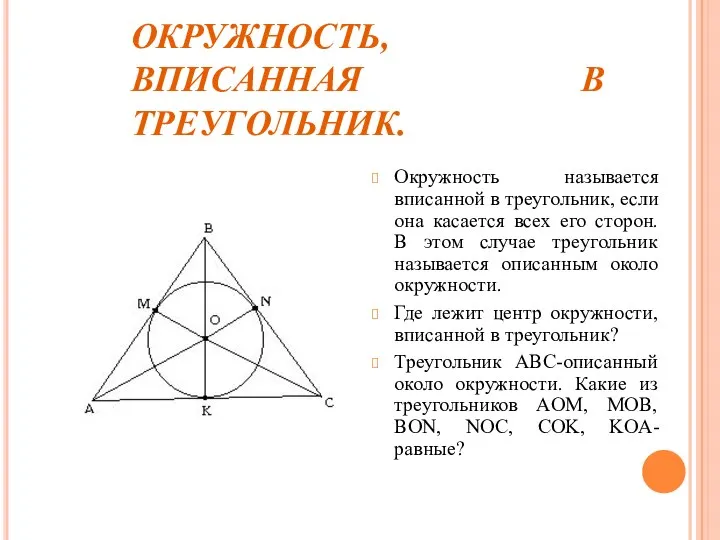
- 12. ОКРУЖНОСТЬ, ВПИСАННАЯ В ТРЕУГОЛЬНИК. Окружность называется вписанной в треугольник, если она касается всех его сторон. В
- 14. Скачать презентацию





 Симметрия. Закономерности
Симметрия. Закономерности Понятие десятичной дроби
Понятие десятичной дроби Углы. Тест
Углы. Тест Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса
Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса Тригонометрические функции
Тригонометрические функции Сумма углов треугольника
Сумма углов треугольника Metode numerice (Curs 2)
Metode numerice (Curs 2) Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Понятие доли
Понятие доли Уравнение прямой
Уравнение прямой Начальные геометрические сведения. Решение задач
Начальные геометрические сведения. Решение задач Статистическая теория радиотехнических систем. Вероятностные характеристики огибающей и фазы узкополосногонормального процесса
Статистическая теория радиотехнических систем. Вероятностные характеристики огибающей и фазы узкополосногонормального процесса Параллелограмм и трапеция
Параллелограмм и трапеция ЕГЭ 2020. Решение задания №10
ЕГЭ 2020. Решение задания №10 Целые уравнения. Уравнения с модулем. Угол между прямыми в пространстве. ЕГЭ 11 - 1. Занятие 1
Целые уравнения. Уравнения с модулем. Угол между прямыми в пространстве. ЕГЭ 11 - 1. Занятие 1 Множества. Операции над ними
Множества. Операции над ними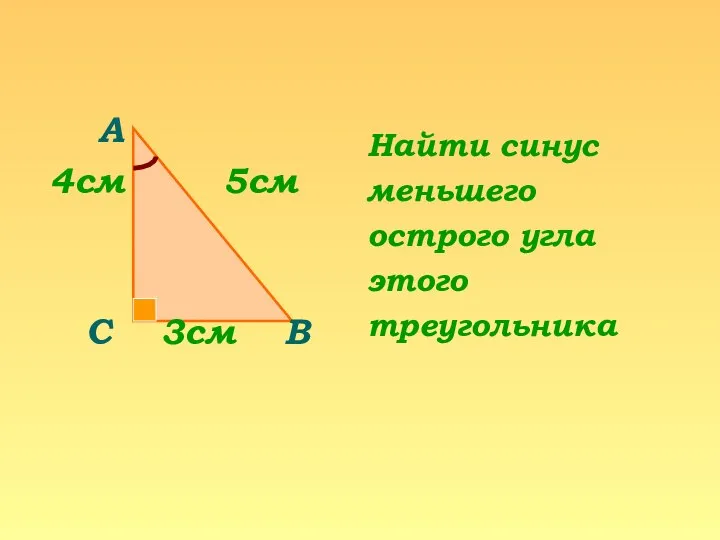 Устная работа на уроке геометрии
Устная работа на уроке геометрии Свойства функций
Свойства функций Таблица умножения восьми
Таблица умножения восьми Тестирование МЦКО. Задания с развернутым ответом. (7 класс)
Тестирование МЦКО. Задания с развернутым ответом. (7 класс) Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений
Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений  КВМ: Здесь затеи и задачи
КВМ: Здесь затеи и задачи Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые Задачи на проценты
Задачи на проценты Среднее арифметическое
Среднее арифметическое Скалярное произведение векторов
Скалярное произведение векторов Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Поле чудес. Геометрия 9 класс
Поле чудес. Геометрия 9 класс