Основы теории вероятностей или случайные события ( лекция 2)

Следствия теорем сложения и умножения
Пример совместных событий: A – появление 4х очков;
B – появление чётного числа очков.

Теорема сложения вероятностей трёх совместных событий
0,1 0,2 0,3 0,02 0,03
0,06 0,006 = 0,496
По формуле для вероятности противоположного события:
1-(1-0,1)*(1-0,2)*(1-0,3)=0,496

Следствия теорем сложения и умножения

Решение задач через формулу полной вероятности

Формула Байеса
Вероятность B при наступлении A (апостериорная, «после-опытная» вероятность)
Событие B также часто называют гипотезой!!
Априорная, «до-опытная» вероятность B)
Полная вероятность A

Решение задач по формуле Байеса
Апостериорная вероятность события B3
Полная вероятность события A
Априорная вероятность B3
Усл.вер-ть A
Вероятность выбора 3го поставщика
Вероятность того, что у 3го поставщика помидор свежий

Формула Бернулли

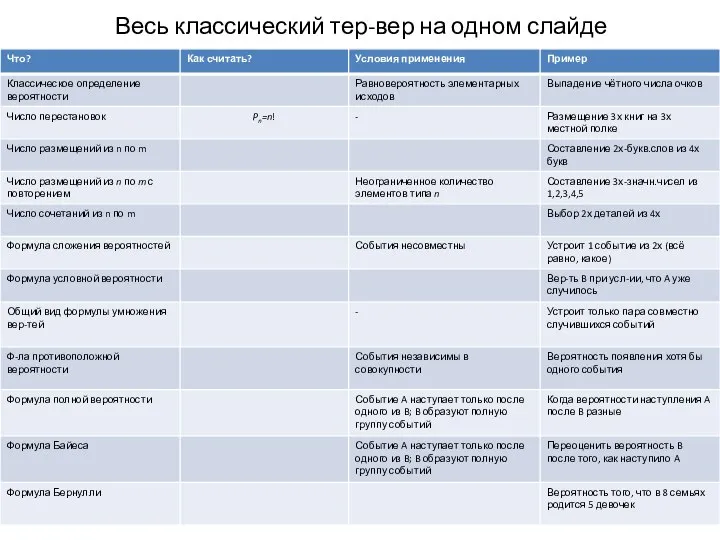
Весь классический тер-вер на одном слайде

Парадокс дней рождения
Ну надо же, мы родились в один день! Какое невероятное совпадение!
Вовсе нет! Анна пригласила столько народу, что вероятность такого совпадения больше 50%!
ВОПРОС: Сколько же людей минимум должна была пригласить на вечеринку Анна?