Содержание
- 2. Лінійною системою m рівнянь з n невідомими х1, х2,…хn називається система виду де числа а11, а12,…аmn
- 3. Сумісна система, що має єдиний розв’язок, називається визначеною, система, що має більш ніж один розв’язок –
- 4. Система рівнянь (2.1) еквівалентна системі Ах=b, записаній в матричній формі. Якщо |А| ≠0, то матриця А
- 5. Приклад: Розв’язати систему рівнянь матричним методом. отже, А – невироджена і існує Aij=(-1)i+j Мij.
- 7. . 2.3 Правило Крамера Матрична рівність х =А-1b можна записати у вигляді звідки, з урахуванням теореми
- 8. Правило Крамера: якщо визначник системи рівнянь відмінний від 0, то вона має єдиний розв’язок який визначається
- 9. Приклад: Розв’язать систему рівнянь за формулами Крамера. Отже, система має єдиний розв’язок, визначений за формулами Крамера
- 10. Дослідження системи Якщо det≠ 0, то система має єдиний розв’язок. Якщо det = 0 і принаймні
- 11. 2.4 Метод Гаусса Елементарними перетвореннями матриці називаются наступні операції: а) перестановка двох рядків матриці; б) множення
- 12. Розглянемо систему лінійних рівнянь або до трапецієподібного виду Її розширену матрицю елементарними перетвореннями над рядкаси можна
- 13. Матриця (2.2) відповідає перетвореній системі В цьому випадку, починаючи з останнтього рівняння, знаходим послідовно значения невідомих
- 14. Приклад: Розв’язать систему рівнянь методом Гаусса. Розширена матриця системи має вид: Переставим другий рядок на місце
- 15. Від другого рядка помноженого на 6 віднімемо 3-й: Матриця зведена до трикутного виду, їй відповідає перетворена
- 16. Для трапецієвидної матриці (2.3) перетворена система має вид: Звідки знаходим Надаючи змінним xm+1, xm+2,…xn довільні значення,
- 17. Приклад: За допомогою метода Гаусса розвязать систему Оскільки, rang(A)=3 Основна матриця системи має вид: Поміняємо перший
- 19. Скачать презентацию




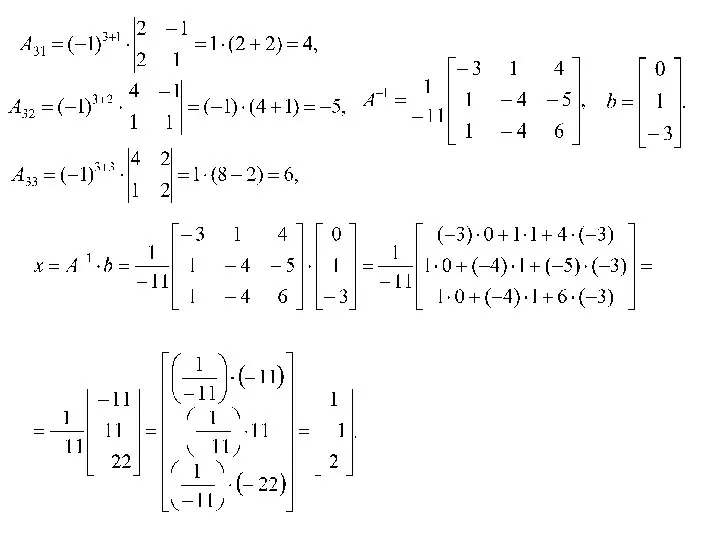











 Угловой коэффициент прямой
Угловой коэффициент прямой Циклический алгоритм
Циклический алгоритм Ноль и нуль
Ноль и нуль Все способы решения тригонометрических уравнений
Все способы решения тригонометрических уравнений Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Сложение и вычитание в пределах первого десятка. Интерактивная игра-соревнование Поиграем в баскетбол
Сложение и вычитание в пределах первого десятка. Интерактивная игра-соревнование Поиграем в баскетбол Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК) Задача 3. Построить матрицу поворота
Задача 3. Построить матрицу поворота Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью Устный счёт Живые примеры от Гнома
Устный счёт Живые примеры от Гнома Произведение многочленов
Произведение многочленов На сколько больше? На сколько меньше?
На сколько больше? На сколько меньше? Преобразование графиков функций
Преобразование графиков функций История возникновения комплексных чисел
История возникновения комплексных чисел Степень с натуральным показателем
Степень с натуральным показателем Презентация на тему Рациональные числа и действия над ними
Презентация на тему Рациональные числа и действия над ними  Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15 Измерение ёмкости (вместимости). 3 класс
Измерение ёмкости (вместимости). 3 класс Выберите чётные числа (Использование триггеров в презентации)
Выберите чётные числа (Использование триггеров в презентации) Практическая работа
Практическая работа Признаки возрастания и убывания функции. Экстремум функции
Признаки возрастания и убывания функции. Экстремум функции Разнообразие форм контроля выполнения домашнего задания
Разнообразие форм контроля выполнения домашнего задания Доказательство тождеств
Доказательство тождеств Первообразная функции
Первообразная функции О сохранении и нарушении равносильности при решении уравнений и неравенств
О сохранении и нарушении равносильности при решении уравнений и неравенств График функции у = ах 2 + bх + qс
График функции у = ах 2 + bх + qс Тренажер для устного счета Простейшие тригонометрические уравнения
Тренажер для устного счета Простейшие тригонометрические уравнения Изучаем цифры и знаки вместе со Смешариками
Изучаем цифры и знаки вместе со Смешариками