Графическое представление и первичная обработка фондовых данных

Классификация временных рядов:
1. По структуре - непрерывные и дискретные данные.
2. По охвату временного интервала - моментные и интервальные.
3. По форме представления уровней – ряды абсолютных, относительных и средних величин.
4. По заполняемости - выделяют полные и неполные временные ряды.

Описательные статистические показатели.
Для представления обобщающих показателей, используются показатели центра распределения, показатели вариа­ции, показатели скошенности (асимметрии) и показатели эксцесса.
Средние величины позволяют сделать вывод о центральном или наиболее общем значении, найденном для совокупности данных. Меры рассеяния (вариации) показывают, как данные распределе­ны вокруг средней. Показатели скошенности (асимметрии) иллюстрируют степень левосторонней асимметрии, т.е. отрицательной, или правосторонней, т.е. положительной, в распределении частот. Показатели эксцесса определяют уровень островершинности или плосковершинности распределения частот.

Если А = 0 и k = 1, то мы получим среднюю арифметическую. Поэтому средняя арифме­тическая иногда называется моментом первого порядка относитель­но нуля. Если же величина А сама является средней арифме­тической и k=2, мы имеем момент второго порядка относительно средней (центральный момент второго порядка), известный как дисперсия, и характеризующий вариацию признака. При А, равном средней, и k = 3 получаем момент третьего порядка относительно средней (центральный момент третьего порядка), который является мерой скошенности, а если k = 4, то определяется момент четвертого порядка относительно средней (центральный момент четвертого порядка), измеряющий эксцесс.

Показатели центра распределения.
Cуществует несколько показателей "средней“ величины, которые особенно интересны в сфере финансов. Это:
мода;
медиана;
средняя арифметическая;
средняя геометрическая.

Мода - это наиболее часто наблюдаемая величина изучаемой переменной. Для ее иллюстрации рассмотрим следующие дан­ные, которые показывают цену акции, выраженную в рублях, в течение 15-дневного периода:
100, 120, 90, 80, 100, 150, 140, 120, 110, 100, 120, 120, 100, 120, 110.
Модой, т.е. наиболее часто повторяющимся наблюдением, является величина 120.

Медиана - это значение наблюдения, которое находится в сере­дине ранжированного ряда данных, т.е. наблюдение, занимаю­щее срединное положение.
Медиана для несгруппированных данных. Для определения ме­дианы в случае несгруппированных данных мы сначала должны расположить их в возрастающем порядке. Покажем это на при­мере, использованном при рассмотрении моды
80, 90, 100, 100, 100, 100, 110, 110, 120, 120, 120, 120, 120, 140, 150.
Так как присутствуют 15 наблюдений, медианой является значение восьмого наблюдения, т.е. величина признака, равная 110.

Средняя арифметическая для несгруппированных данных
Средние показатели динамики - средний уровень ряда, сред­ние абсолютные изменения и ускорения, средние темпы роста - характеризуют тенденцию. Они необходимы при обобщении характеристик тенденции за длительный период, по различным периодам; они незаменимы при сравнении развития за неодинаковые по длительности отрезки времени и при выборе ана­литического выражения тренда.

Средняя арифметическая рассчитывается суммированием всех значений отдельных наблюдений и последующим делением по­лученной суммы на количество наблюдений. Например, допус­тим, что мы желаем подсчитать среднюю арифметическую цены какого-либо актива в течение пяти дней. В данный период мы наблюдаем следующие цены
225 225 240 215 230
Найдем среднюю арифметическую, складывая эти пять значений и деля сумму на число наблюдений. В формализован­ном виде средняя арифметическая выглядит так:

Дисперсия и среднее квадратическое отклонение.
Если средняя арифметическая выбрана как показатель центра распределения, то соответствующими показателями вариации являются дисперсия и среднее квадратическое отклонение. Дис­персия широко применяется в финансовых расчетах как мера риска и неопределенности. Сред­нее квадратическое отклонение ис­пользуется как мера изменчивости в ценообразовании, например, опционов.

Формула для дисперсии:
Среднее квадратическое отклонение:

Коэффициент вариации. Среднее квадратическое отклонение выражается в единицах из­мерения, лежащих в основе расчета. Таким образом, при срав­нении степени вариации переменных должны быть учтены раз­личия в величине этих переменных. Для этого нужно рассчитать коэффициент вариации. Он находится как отношение:

Коэффициент асимметрии
Иногда бывает важно знать, есть ли смещения в рассеянии данных. Ин­дикатор этих смещений - скошенность (асимметрия) данных. В случае положительной асимметрии распределение имеет длинную правую ветвь. Средняя величина дохода больше медиа­ны, которая в свою очередь больше моды. Значение средней больше медианы и моды, потому что на нее повлияли несколько очень больших значений доходов.
Отрицательная асимметрия проявляется в виде более длинной левой ветви, а величина средней меньше медианы и моды. Боль­шинство наблюдений распределения имеют значения больше средней, но величина средней снижается из-за нескольких очень малых наблюдений.

Коэффициент асимметрии
Показателем асимметрии, который наиболее пригоден для применения в случае сгруппированных данных, является ко­эффициент асимметрии, основанный на расчете моментов рас­пределения. Он определяется с помощью центрального момента третьего порядка и деления его на куб среднего квадратического отклонения, что можно представить следующей формулой:

Эксцесс
Показатели эксцесса описывают пиковость распределения. Распределения, имеющие более выраженный пик, чем у нормального распределения, называются островершинными. Те же распре­деления, у которых степень вытянутости вдоль оси ординат меньше, чем у нормальной кривой, называются плосковершинными, а рас­пределения, которые похожи на нормальное, - средневершинными.
Островершинные распределения можно увидеть в доходах активов, когда наблюдаются периодические скачки в ценах на эти активы.

Эксцесс
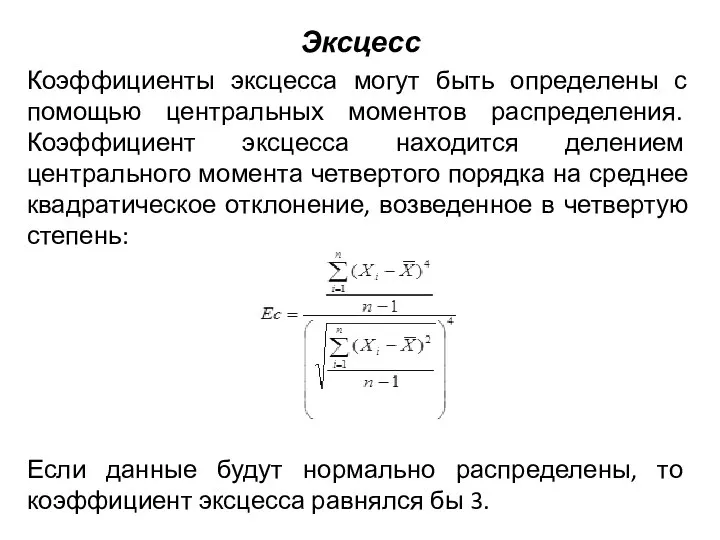
Коэффициенты эксцесса могут быть определены с помощью центральных моментов распределения. Коэффициент эксцесса находится делением центрального момента четвертого порядка на среднее квадратическое отклонение, возведенное в четвертую степень:
Если данные будут нормально распределены, то коэффициент эксцесса равнялся бы 3.

Показатели статистической связи
Введем понятие ковариации, которая показывает, как две случайные переменные ведут себя по отношению одна к другой:
Ковариация:
Коэффициент корреляции: