Интервальные вычисления. Лекция 11

Лекция по курсу
«Машинная арифметика в рациональных числах»
на тему интервальные вычисления
2020

Правила интервальные вычисления
(Достоверные вычисления)
Вычисления с интервалами:

Интервальные вычисления
(Достоверные вычисления)
Автоматическая верификация результатов
Доказательство корректности вычислительных задач.
(гипотезы теории хауса, Кеплера и др.)
(Не влияют на корректность алгоритма)
Направленные округления:
1. Нижняя граница – результат округления до ближайшего машинного числа с плавающей точкой с недостатком
2. Верхняя граница – результат округления до ближайшего машинного числа с плавающей точкой с избытком

Интервальные вычисления
(Достоверные вычисления)
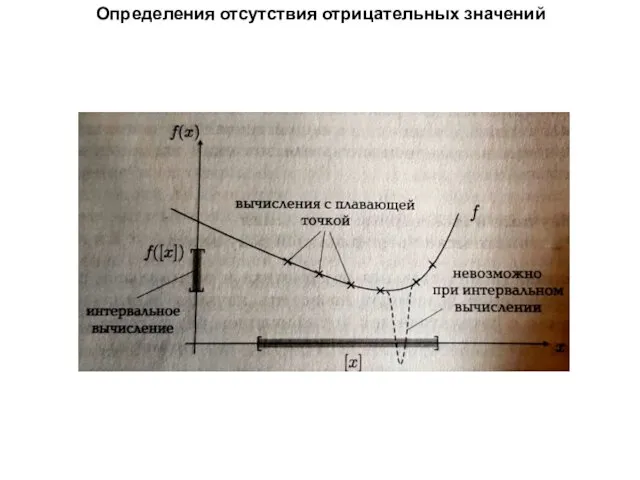
Проблема расширения интервалов в процессе вычислений.
Примеры задач где они применяются
Гарантированное нахождение всех нулей нелин. функции
Глобальная оптимизация с подтверждением правильности нахождения минимума

Определения отсутствия отрицательных значений

PASCAL –XSC, C-XSC
PASCAL Extension for Scientific Computation
Некоторые типы данных:
complex, interval, cinterval, rvector, cvector, ivector, rmatrix, imatric
dotprecision – числа с фиксированной точкой, покрывающие весь возможный диапазон представления чисел c плавающей точкой.
(< +- Мантисса E показатель) – округление с недостатком
(> +- Мантисса E показатель) – округление с избытком
yyy…yyy, xxxxx..x (38 – кол десят разрядов целой части, 38 – кол дес дробной части)
0,123
123,456
(X,Y) = x1*y1+x2*y2+…+xn*yn
X = (x1,x2,…,xn)
Y = (y1,y2,…,ym)

PASCAL –XSC, C-XSC
Интревальная арифметика – модуль i_ari
Арифметика матриц и векоторов mv_ari
(< +- Мантисса E показатель) – округление с недостатком
(> +- Мантисса E показатель) – округление с избытком