Содержание
- 2. Повторение Что такое призма? Что может являться в основании призмы? Что является боковой стороной призмы? Призма
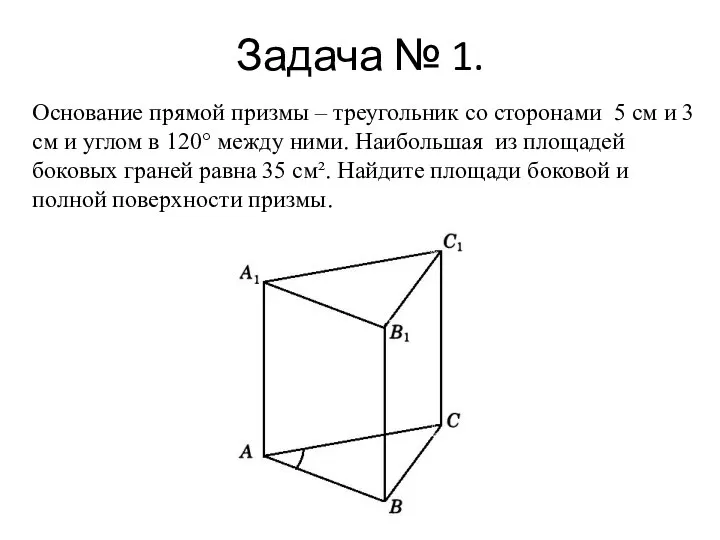
- 3. Задача № 1. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и
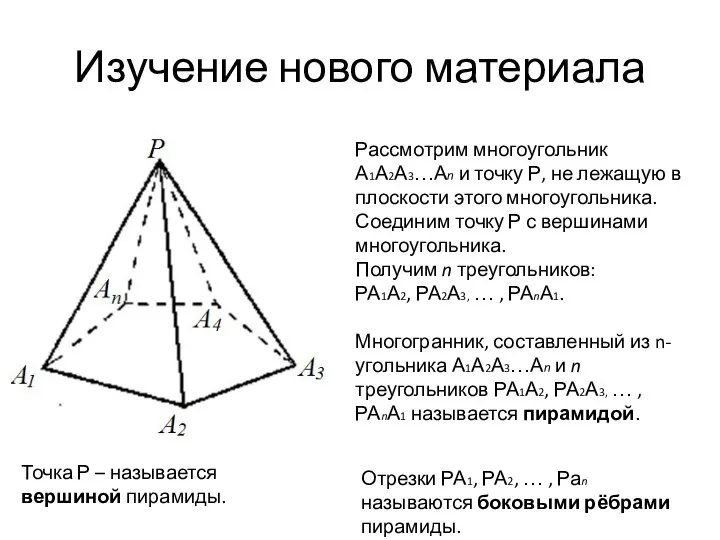
- 4. Изучение нового материала Рассмотрим многоугольник А1А2А3…Аn и точку Р, не лежащую в плоскости этого многоугольника. Соединим
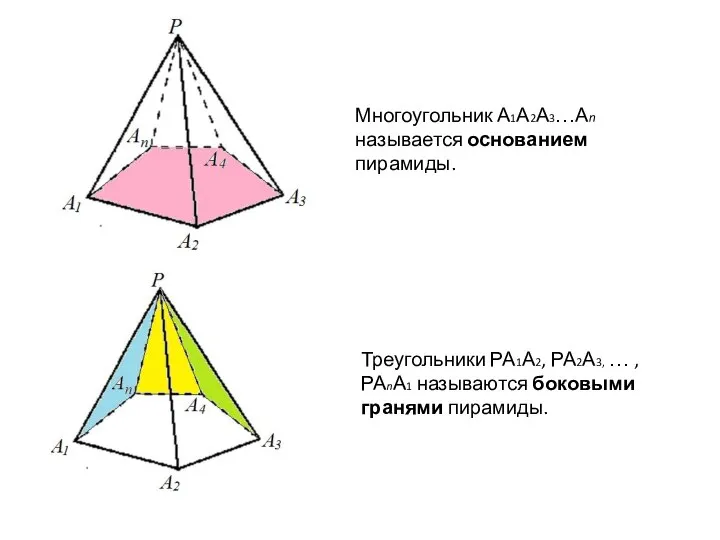
- 5. Многоугольник А1А2А3…Аn называется основанием пирамиды. Треугольники РА1А2, РА2А3, … , РАnА1 называются боковыми гранями пирамиды.
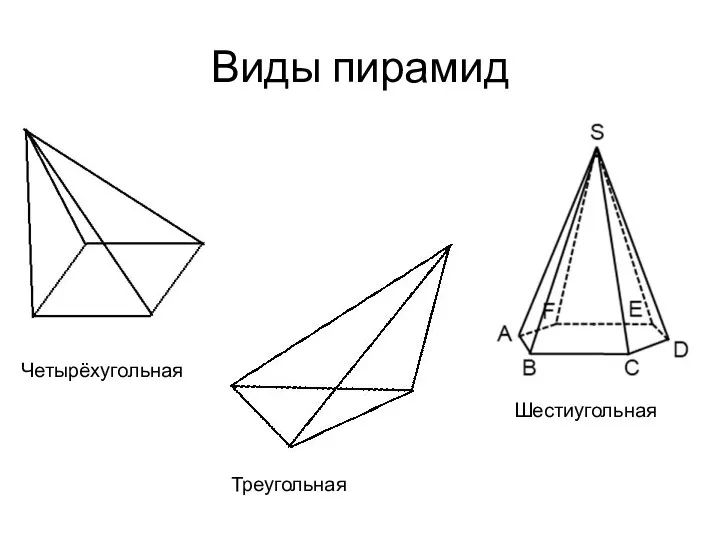
- 6. Виды пирамид Четырёхугольная Треугольная Шестиугольная
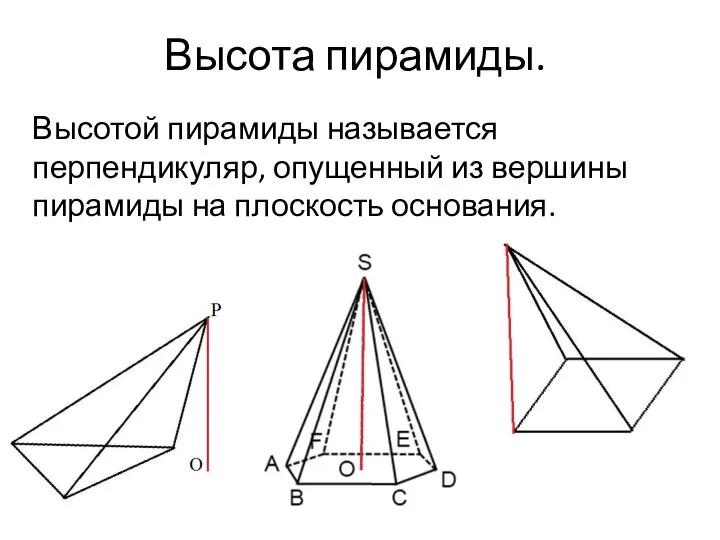
- 7. Высота пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
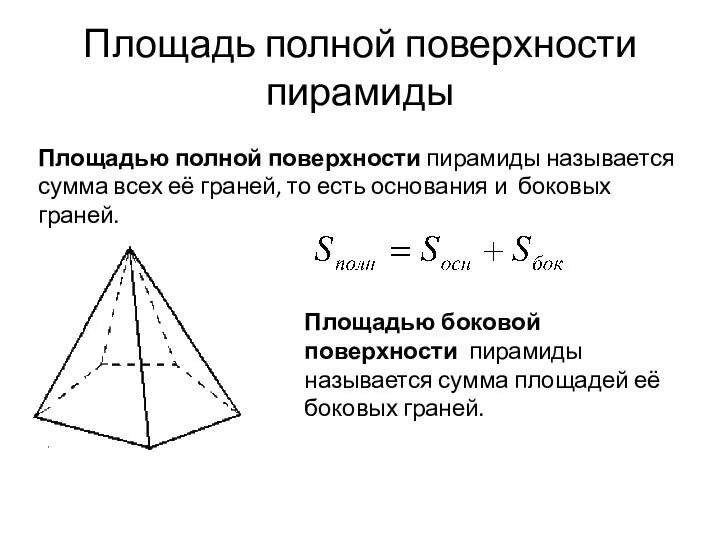
- 8. Площадь полной поверхности пирамиды Площадью полной поверхности пирамиды называется сумма всех её граней, то есть основания
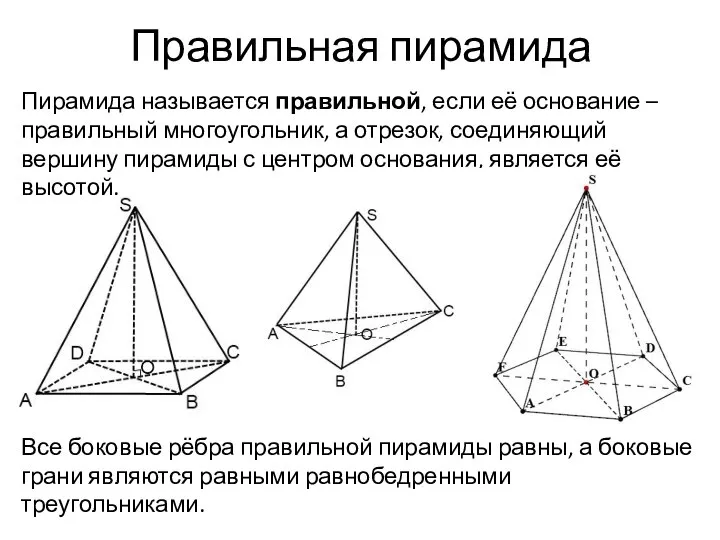
- 9. Правильная пирамида Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды
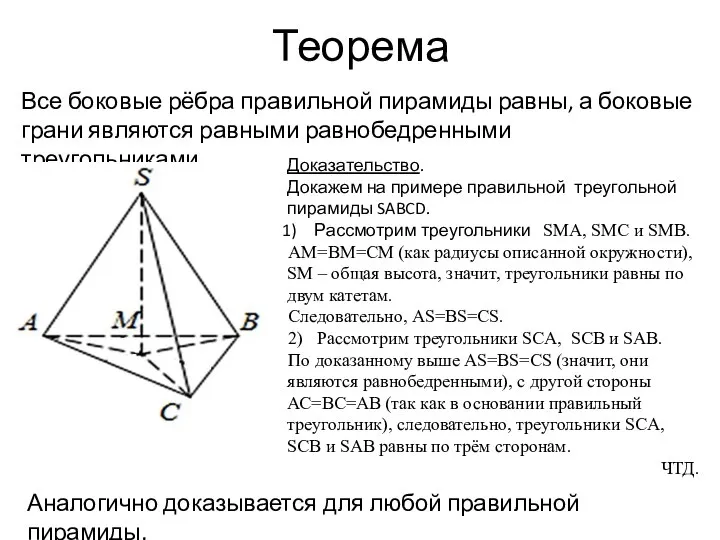
- 10. Теорема Все боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. Доказательство. Докажем
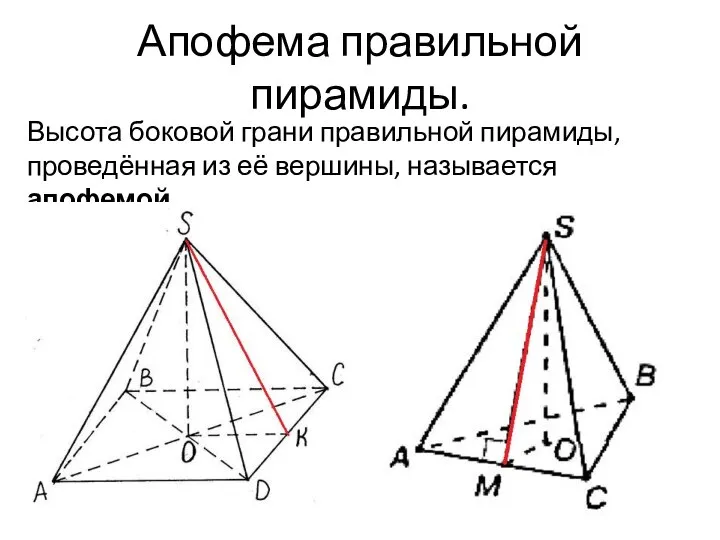
- 11. Апофема правильной пирамиды. Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
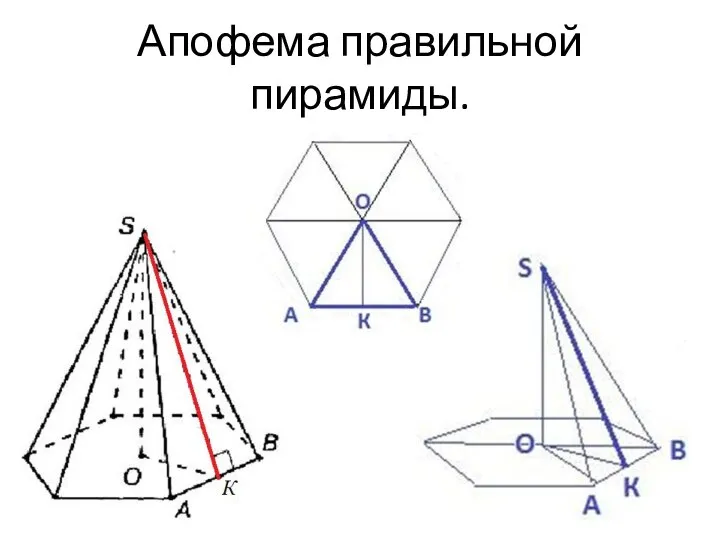
- 12. Апофема правильной пирамиды.
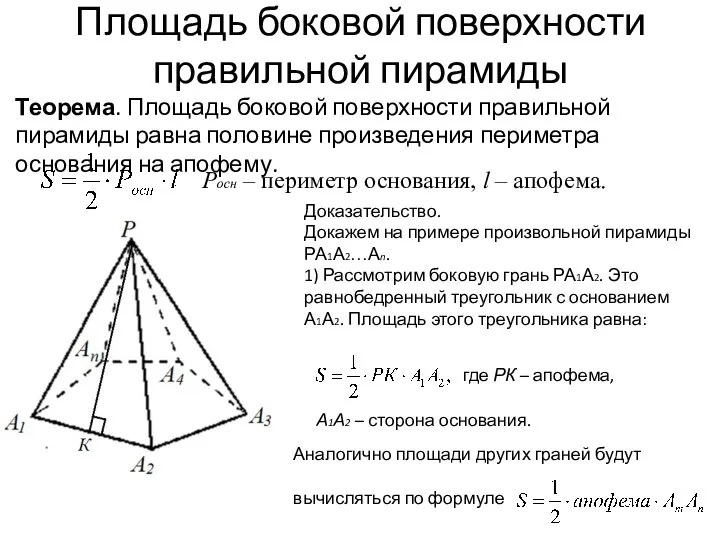
- 13. Площадь боковой поверхности правильной пирамиды Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания
- 14. Площадь боковой поверхности правильной пирамиды Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания
- 15. Закрепление Что такое пирамида? Что такое основание пирамиды? Что может лежать в основании пирамиды? Из какой
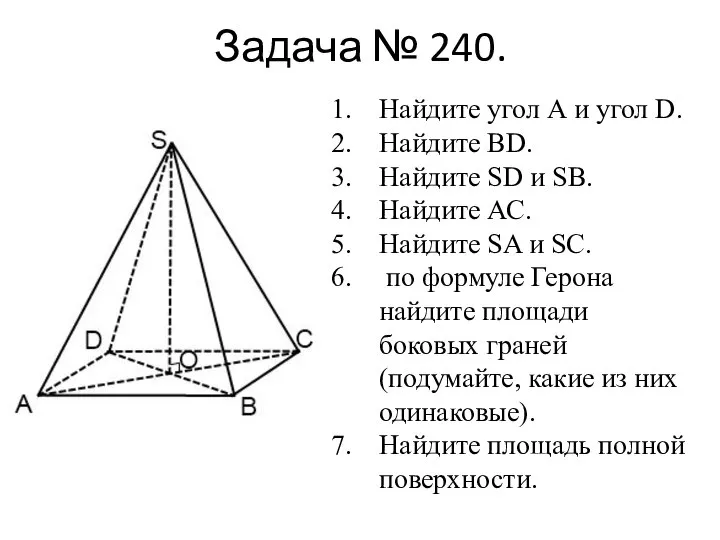
- 16. Задача № 240. Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а
- 17. Задача № 240. Найдите угол А и угол D. Найдите ВD. Найдите SD и SB. Найдите
- 19. Скачать презентацию




 Состав числа 9
Состав числа 9 Логарифмы
Логарифмы Интеллектуальная игра по математике: ТОК. Для учащихся 8-го класса
Интеллектуальная игра по математике: ТОК. Для учащихся 8-го класса Презентация на тему Задачи на приведение к единице (3 класс)
Презентация на тему Задачи на приведение к единице (3 класс)  Элективный курс. Алгебра 11 класс. Уроки 10
Элективный курс. Алгебра 11 класс. Уроки 10 Сумма углов треугольника. Виды треугольников
Сумма углов треугольника. Виды треугольников izmerenie_otrezkov_7_klass
izmerenie_otrezkov_7_klass Калькуляционная карточка. Тесто заварное
Калькуляционная карточка. Тесто заварное Задачи на движение
Задачи на движение Статистические гипотезы и их проверка
Статистические гипотезы и их проверка Деление круглых сотен на число 100
Деление круглых сотен на число 100 Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Шахматы и математика
Шахматы и математика Методы решения оптимизационных задач
Методы решения оптимизационных задач Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Приёмы сложения однозначных чисел с переходом через десяток
Приёмы сложения однозначных чисел с переходом через десяток Модели решения функциональных и вычислительных задач. Методы и технологии моделирования
Модели решения функциональных и вычислительных задач. Методы и технологии моделирования Презентация на тему Деление суммы на число (3 класс)
Презентация на тему Деление суммы на число (3 класс)  Производная. Тест по алгебре
Производная. Тест по алгебре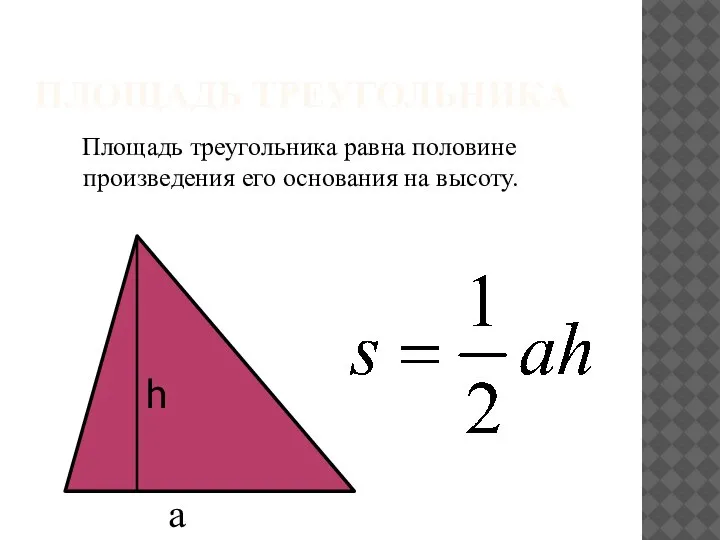 Площадь треугольника
Площадь треугольника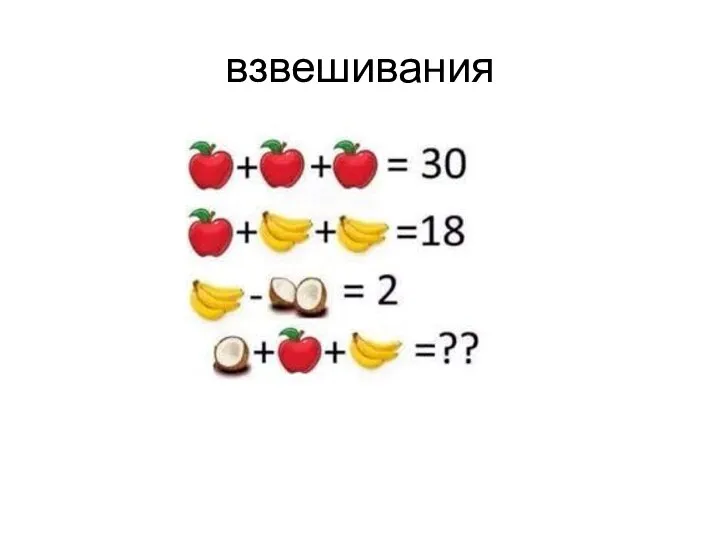 Взвешивания. Домашнее задание 1 класс
Взвешивания. Домашнее задание 1 класс Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса Элементы аналитической геометрии на плоскости
Элементы аналитической геометрии на плоскости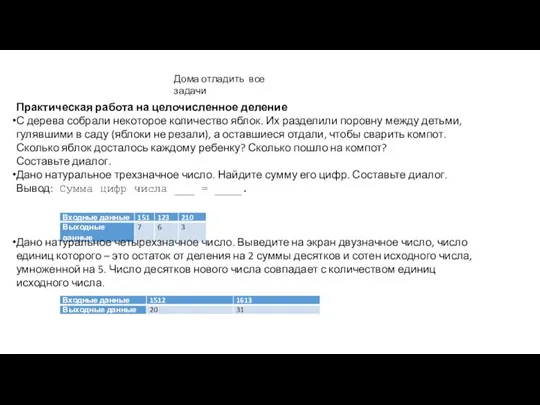 Практическая работа на целочисленное деление
Практическая работа на целочисленное деление Геометрические преобразования в пространстве
Геометрические преобразования в пространстве Реальная математика. Геометрия. ГИА-2014
Реальная математика. Геометрия. ГИА-2014