Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)

Добрый день, ребята!
Сегодня на уроке математики мы начинаем изучение нового раздела «Натуральные числа».
Натуральными называют числа, которые используют при счете предметов. И прежде,
чем мы познакомимся с ними поближе, давайте узнаем, а как же люди научились считать.

Учиться считать люди начали в незапамятные времена
Учителем у них была сама жизнь

Никто не знает, когда впервые появились счёт и число
Но уже несколько десятков тысяч лет назад
люди собирали плоды и ягоды
Охотились на диких животных
Делали каменные ножи и топоры, наконечники

Людям приходилось охотиться
на крупных зверей: лося, зубра

Учиться считать требовала жизнь
Надо было знать, хватит ли добычи до следующей охоты
Много ли пойманной рыбы

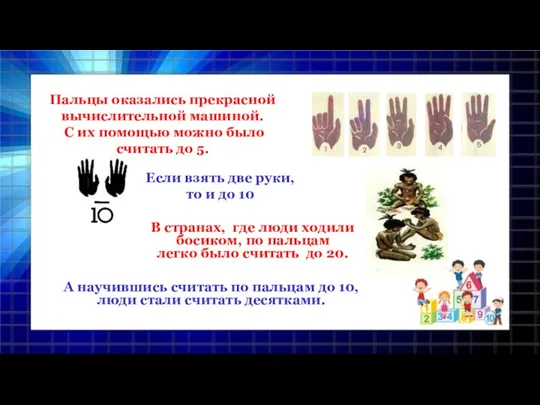
Так начинали учиться считать, пользуясь тем, что дала им сама природа, – собственной пятернёй
Название чисел сначала показывали на пальцах

Названия чисел поначалу были у одного и двух
Придумывая имя числу 1, исходили
из того, что Солнце на небе одно.

Названия для числа 2 во многих языках связано с предметами, встречающимися попарно:
крыльями
глазами
руками

«Три да четыре даёт семь» – получили люди,
заметив, что ковш Большой Медведицы
складывается из трёх звёзд ручки
и четырёх остальных звёзд.

А научившись считать по пальцам до 10, люди стали считать десятками.
Пальцы оказались прекрасной вычислительной машиной.
С их помощью можно было считать до 5.
Если взять две руки,
то и до 10
В странах, где люди ходили
босиком, по пальцам
легко было считать до 20.

Проходили многие-многие годы. Менялась жизнь человека.
Людям приходилось всё чаще
сталкиваться с большими числами.
Нужно было придумать,
как их записывать.
Люди приручили животных,
на земле появились первые скотоводы, земледельцы.

Первым способом «записи» чисел были
глиняные
шарики
и другие
фигурки
зарубки
на палке

Индейцы в Америке изображали числа
с помощью узелков на верёвках

Древний Египет
15
Числа первого десятка
записывали
соответствующим
количеством палочек
Десять обозначалось скобочкой
в виде подковы
Догадаетесь, какое это число?

Сотню обозначали крючком
Так обозначали тысячу
А так обозначали миллион
Сто тысяч обозначали лягушкой
Древний Египет

Записывать таким способом числа было
не очень удобно и совсем неудобно было их складывать, вычитать, умножать, делить
Древний Египет

В Древнем Вавилоне записывали числа,
выдавливая значки палочкой на глиняной дощечке

Система счёта у народов майя

Знак для 5 – раскрытая ладонь
Знак для 10 – две раскрытые ладони
Система записи чисел в Древнем Риме

В Древней Руси буква «а» обозначала число 1
Буква «б» обозначала число 2
Для обозначения чисел 10, 20,100,…, 900 использовались буквы
Для отличия чисел от букв использовали знак «титло»
титло
Славянские цифровые знаки – буквы с титлами
Запись чисел в Древней Руси

Как видите, человечество к современной системе счисления проделало нелегкий путь.
Представьте себе арифметические действия с древнерусскими числами или с числами народов майя! Даже с уже привычными нам римскими цифрами это не так просто.
Сегодняшний урок еще раз докажет нам, насколько удобна привычная нам
десятичная система счисления.

Современная десятичная позиционная система счисления является величайшим достижением человечества.
С помощью этой системы записывают сколь угодно большие числа, используя всего лишь десять различных цифр.
Это возможно потому, что одна и та же цифра имеет различные значения
в зависимости от ее позиции в числе.

Цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 называют арабскими. Однако изобрели их совсем не арабы,
а индусы, и цифры эти по сути являются индийскими.
Арабы просто высоко оценили преимущества этих цифр по сравнению с римской и греческой системами, которые считались на тот момент самыми совершенными в мире.
Неудивительно, что и европейцы переняли арабские цифры. Это какие же мудрые ученые
были на Востоке! Сегодня это кажется очень удивительным.

Перейдем от истории к математике

Наименьшим натуральным числом является число 1. Наибольшего натурального числа не существует.
Все натуральные числа, записанные в порядке возрастания, образуют ряд натуральных чисел:
1, 2, 3, 4, 5, 6, 7, …
Натуральные числа записывают при помощи цифр. Всего цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Натуральные числа, записанные одной цифрой, называют однозначными, двумя цифрами –
двузначными, тремя цифрами – трехзначными и т. д.

Как прочитать натуральное число?
Например, число 25348603549
Нужно разбить его справа налево на группы по три цифры: 25.348.603.549
Эти группы называют классами: справа налево идут
класс единиц, класс тысяч, класс миллионов, класс миллиардов и т. д.
25.348.603.549
класс
единиц
класс
тысяч
класс
миллионов
класс
миллиардов

Каждый класс состоит из трех разрядов: единицы, десятки, сотни.
25.348.603.549
Таким образом, число 25 348 603 549 читают:
двадцать пять миллиардов триста сорок восемь миллионов шестьсот три тысячи пятьсот сорок девять.
единицы
единицы
единицы
единицы
десятки
десятки
десятки
десятки
сотни
сотни
сотни

А как записать натуральное число?
Прочитайте числа:
пятьсот семнадцать миллиардов двести шестьдесят семь миллионов сто восемьдесят две тысячи
триста сорок восемь;
восемь миллиардов пятнадцать миллионов четыреста две тысячи шесть;
двенадцать миллиардов пять тысяч четыре.

Рассмотрим таблицу классов и разрядов:
Запишем в нее число:
пятьсот семнадцать миллиардов
двести шестьдесят семь миллионов
сто восемьдесят две тысячи
триста сорок восемь
5
1
7
2
6
7
1
8
2
3
4
8
.
.
.

Повторим тот же алгоритм с другим числом:
Обратите внимание: в классе миллионов отсутствуют сотни.
Но в каждом классе ВСЕГДА должно быть ТРИ цифры,
поэтому в отсутствующий разряд записываем 0.
восемь миллиардов
пятнадцать миллионов
четыреста две тысячи
шесть
8
0
1
5
4
0
2
0
0
6
.
.
.
В классе единиц отсутствуют и десятки, и сотни.
Но в этом классе также должно быть ТРИ цифры,
поэтому в отсутствующие разряды записываем нули.

Повторим еще раз этот алгоритм:
В классе тысяч отсутствуют десятки и сотни, в отсутствующие разряды записываем нули.
двенадцать миллиардов
пять тысяч
четыре
1
0
0
0
0
0
5
0
0
4
.
.
.
В классе единиц отсутствуют десятки и сотни,
в отсутствующие разряды записываем нули.
2
Почему в таблице остались пустые клетки? Потому что число не содержит класса миллионов. Значит, все разряды этого класса заполняем нулями.

Любое натуральное число можно представить
в виде суммы. Например, число 25 367: 25 367 = 20 000 + 5 000 + 300 + 60 + 7
Кроме того, мы знаем, что число 25 367 содержит:
2 десятка тысяч, 5 тысяч, 3 сотни, 6 десятков и 7 единиц.
Заметим, что:
20 000 = 2 · 10 000 – это и есть 2 десятка тысяч;
5 000 = 5 · 1 000 – это 5 тысяч;
300 = 3 · 100 – это 3 сотни;
60 = 6 · 10 – это 6 десятков;
7 = 7 · 1 – это 7 единиц.

Тогда представление в виде суммы можно продолжить. Получим:
Такое равенство:
25 367 = 2 · 10 000 + 5 · 1 000 + 3 · 100 + 6 · 10 + 7 · 1
называют записью числа 25 367
в виде суммы разрядных слагаемых.
25 367 =
20 000 + 5 000 + 300 + 60 + 7 =
= 2 · 10 000 + 5 · 1 000 + 3 · 100 + 6 · 10 + 7 · 1
Обратите внимание, что перенести выражение на новую строку можно так:
знак «=» записать в конце строки, затем еще раз – в начале строки.
Так мы показываем, что это не новое выражение, а продолжение предыдущего.
Перенести можно знаки «+», «–» или «=». Знаки умножения и деления НЕ ПЕРЕНОСЯТ.

Запишите в тетради
Двадцать первое сентября
Классная работа
Тема: «Чтение и запись натуральных чисел»
Многие из вас уже получили учебники. Сегодняшние задания мы будем выполнять по этим учебникам, и нумерация будет соответствующая.
Напоминаю, номер записываем посередине строки: № 1, № 2, № 3 и т. д.
Для тех, кто учебники еще не получил, текст задания будет приведен в полном виде. Переписывать его НЕ НУЖНО (для удобства он будет
выделен красным цветом).
Итак, текст, записанный красным, только читаем.
Текст, записанный темно-синим, переписываем в тетрадь.

№ 6
Запишите число, которое в натуральном ряду следует за числом: 1) 34; 2) 246; 3) 8297.
35;
247;
8298.
№ 8
Запишите число, которое в натуральном ряду предшествует числу: 1) 58; 2) 631; 3) 4500.
57;
630;
4499.

№ 10
Сколько чисел стоит в натуральном ряде между числами: 1) 6 и 24; 2) 18 и 81?
Для первой пары чисел давайте просто посчитаем:
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 – 17 чисел.
Заметим, что 24 – 6 = 18, то есть таким действием мы правильного ответа не получим. А каким получим? Посмотрите на схему:
Очевидно, чтобы ответить на поставленный вопрос, нужно от
23 первых чисел отнять 6 первых чисел.
23 – 6 = 17 (чисел);
80 – 18 = 62 (числа).

№ 20 (устно)
Какая цифра не может стоять первой в записи натурального числа?
Цифра 0.
№ 21
Назовите разряд, в котором стоит цифра 4 в записи числа: 1) 34; 2) 246; 3) 473; 4) 24 569.
единицы;
десятки;
сотни;
тысячи.

№ 20 (устно)
Какая цифра не может стоять первой в записи натурального числа?
Цифра 0.
№ 21
Назовите разряд, в котором стоит цифра 4 в записи числа: 1) 34; 2) 246; 3) 473; 4) 24 569.
единицы;
десятки;
сотни;
тысячи.

№ 22 (устно)
Прочитайте число:
1) 234 642; 5) 6 704 917 320;
2) 502 013; 6) 72 016 050 400;
3) 9 145 679; 7) 491 872 653 000;
4) 105 289 001; 8) 305 002 800 748.
По возможности прочитайте числам родителям, пусть они проверят правильность.

№ 23
Запишите цифрами число:
1) 34 миллиона 384 тысячи 523;
2) 85 миллионов 128 тысяч 23;
3) 16 миллионов 26 тысяч 4;
4) 6 миллионов 60 тысяч 17;
5) 8 миллиардов 801 миллион 30 тысяч 5;
6) 22 миллиарда 33 миллиона 418;
7) 251 миллиард 538;
8) 46 миллиардов 854;
9) 607 миллиардов 3.
Постарайтесь записать самостоятельно, затем
сверьтесь с записью на следующим слайде.

№ 23
1) 34.384.523;
2) 85.128.023;
3) 16.026.004;
4) 6.060.017;
5) 8.801.030.005;
6) 22.033.000.418;
7) 251.000.000.538;
8) 46.000.000.854;
9) 607.000.000.003.
Будьте внимательны, на одном из следующих уроков мы напишем самостоятельную работу такого же типа, на запись чисел.

№ 25
Запишите цифрами число:
1) сорок шесть миллиардов четыреста пятьдесят семь миллионов
семьсот двадцать семь тысяч триста восемьдесят восемь;
2) шестьсот тридцать два миллиарда двести четыре миллиона
тридцать пять тысяч сорок семь;
3) сто пять миллиардов пятьсот тридцать девять тысяч сто;
4) тридцать миллиардов двадцать тысяч девяносто;
5) восемь миллиардов семь миллионов пятнадцать тысяч четырнадцать;
6) один миллиард две тысячи два.
Постарайтесь записать самостоятельно, затем
сверьтесь с записью на следующим слайде.

№ 25
1) 46.457.727.388;
2) 632.204.035.047;
3) 105.000.539.100;
4) 30.000.020.090;
5) 8.007.015.014;
6) 1.000.002.002.
Будьте внимательны, на одном из следующих уроков мы напишем самостоятельную работу такого же типа, на запись чисел.

№ 26
Запишите цифрами число:
1) три миллиона триста тридцать три тысячи триста тридцать три;
2) три миллиона триста тысяч;
3) три миллиона три тысячи;
4) три миллиона тридцать;
5) три миллиона тридцать тысяч триста;
6) три миллиона три тысячи три;
7) три миллиона три.
Постарайтесь записать самостоятельно, затем
сверьтесь с записью на следующим слайде.

№ 26
1) 3.333.333;
2) 3.300.000;
3) 3.003.000;
4) 3.000.030;
5) 3.030.300;
6) 3.003.003;
7) 3.000.003.

№ 30
Запишите в виде суммы разрядных слагаемых число:
846; 4) 791 105;
2375; 5) 32 598 009;
12 619; 6) 540 007 020.
Постарайтесь записать примеры 1), 2) и 3) самостоятельно, затем сверьтесь с записью на следующим слайде и примеры 4), 5) и 6) внимательно перепишите.

№ 30
1) 846 = 800 + 40 + 6 = 8 · 100 + 4 · 10 + 6 · 1;
2) 2375 = 2000 + 300 + 70 + 5 = 2 · 1000 + 3 · 100 + 7 · 10 + 5 · 1;
3) 12 619 = 10 000 + 2000 + 600 + 10 + 9 = 1 · 10 000 + + 2 · 1000 + 6 · 100 + 1 · 10 + 9 · 1;
4) 791 105 = 700 000 + 90 000 + 1000 + 100 + 5 =
= 7 · 100 000 + 9 · 10 000 + 1 · 1000 + 1 · 100 + 0 · 10 + 5 · 1;
В примере 4) в разряде десятков записан 0, в сумме разрядных слагаемых также указано «0 десятков».
В примерах 5) и 6) попробуем сразу записать сумму
разрядных слагаемых (см. следующий слайд).

5) 32 598 009 = 3 · 10 000 000 + 2 · 1 000 000 + 5 · 100 000 +
+ 9 · 10 000 + 8 · 1000 + 0 · 100 + 0 · 10 + 9 · 1;
Так быстрее, верно?
6) 540 007 020 = 5 · 100 000 000 + 4 · 10 000 000 +
+ 0 · 1 000 000 + 0 · 100 000 + 0 · 10 000 + 7 · 1000 + 0 · 100 +
+ 2 · 10 + 0 · 1.

№ 33
Запишите наибольшее восьмизначное число, а также следующее и предыдущее числа.
99 999 999 – наибольшее восьмизначное число;
99 999 998 – предыдущее;
100 000 000 – следующее.
Это было последнее задание на сегодня. Надеюсь,
все разобрались. На следующих двух слайдах –
домашнее задание.

Домашнее задание
7. Запишите число, которое в натуральном ряду следует за числом:
1) 72; 2) 121; 3) 6459.
9. Запишите число, которое в натуральном ряду предшествует числу:
1) 42; 2) 215; 3) 3240.
11. Сколько чисел стоит в натуральном ряду между числами: 1) 13 и 28; 2) 29 и 111?
24. Запишите цифрами число:
1) 23 миллиона 275 тысяч 649;
2) 56 миллионов 319 тысяч 48;
3) 12 миллионов 20 тысяч 21;
4) 8 миллионов 7 тысяч 3;
5) 6 миллиардов 325 миллионов 800 тысяч 954;
6) 14 миллиардов 52 миллиона 819;
7) 368 миллиардов 742 тысячи;
8) 92 миллиарда 29. Продолжение – на следующем слайде.

Домашнее задание
27. Запишите цифрами число:
1) шестьдесят восемь миллиардов двести сорок девять миллионов девятьсот пятьдесят четыре тысячи семьсот двадцать три;
2) восемьсот четырнадцать миллиардов сто девять миллионов две тысячи тридцать два;
3) триста семь миллиардов шестьсот двадцать одна тысяча четыреста;
4) девяносто миллиардов десять тысяч двадцать;
5) два миллиарда три миллиона четыре тысячи пять;
6) один миллиард одна тысяча один.
31. Представьте в виде суммы разрядных слагаемых число:
1) 34 729; 2) 478 254; 3) 23 487 901.
34. Запишите наименьшее семизначное число, а также
следующее и предыдущее ему числа.
Желаю удачи!