Функция параболы

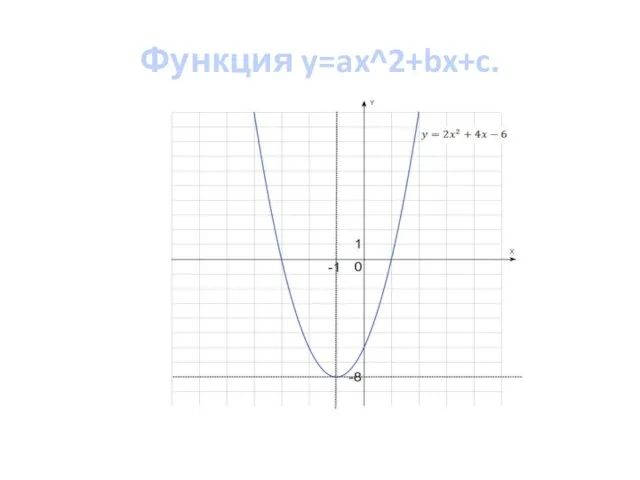
Функция y=ax^2+bx+c.
Для построения графика нужно построить график функции , причем вершина параболы будет находиться в точке с координатами (-l;m).
И так наша функция - парабола.
Осью параболы будет являться прямая
причем координаты вершины параболы по оси абсцисс, как мы можем заметить, вычисляется формулой:
Для вычисления координаты вершины параболы по оси ординат, вы можете пользоваться либо формулой:
Либо напрямую подставить в исходную функцию координату вершины по х:
Как вычислять ординату вершины, опять же выбор за вами, но скорее всего вторым способом посчитать будет проще.

Функция y=ax^2+bx+c.
Если требуется описать какие свойства или ответить на какие то определенные вопросы, то не всегда обязательно строить график функции. Основные вопросы, на которые можно ответить без построения, рассмотрим в следующем примере.
Пример 1. Без построения графика функции
ответьте на следующие вопросы:
а) Укажите прямую служащую осью параболы.
б) Найдите координаты вершины.
в) Куда смотрит парабола? (Вверх или вниз)
Решение.
а) Осью параболы служит прямая
б) Абсцисса вершины

Функция y=ax^2+bx+c.
ординату вершины найдем, непосредственной подстановкой в исходную функцию:
в) График требуемой функции получится параллельным переносом графика - ветви которой смотрят вверх, а значит и ветви параболы исходной функции так же будет смотреть вверх.
Вообще если коэффициент а>0 то ветви смотрят вверх, если коэффициент a<0, то ветви смотрят вниз.

Функция y=ax^2+bx+c.
Пример 2. Построить график функции:
Решение. Найдем координаты вершины параболы:
Отметим координату вершины на оси координат, и в этой точке, как будто в новой системе координат построим параболу .Существует множество способов упрощающих построение графиков параболы.
Мы можем найти две симметричные точки, вычислить значение функции в этих точках, отметить их на координатной плоскости, и соединить их с вершиной, кривой описывающей параболу.
Мы можем, построить ветвь параболы, правее или левее вершины, и потом ее отразить.
Мы можем строить по точкам.

Функция y=ax^2+bx+c.

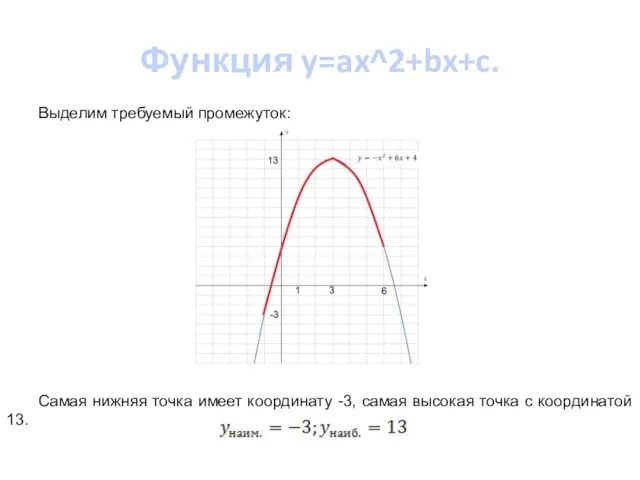
Функция y=ax^2+bx+c.
Пример 1. Найти наибольшее и наименьшее значение функции
на отрезке [-1;6].
Решение. Построим график данной функции, выделим требуемый промежуток и найдем самую нижнюю и самую высокую точку графика функции.
Найдем координаты вершины параболы:
В точке с координатами (3;13), построим параболу

Функция y=ax^2+bx+c.
Выделим требуемый промежуток:
Самая нижняя точка имеет координату -3, самая высокая точка с координатой 13.