a large amount of equations need to be calculated quickly, linear algebra is most likely being used. These applications would include things like graphics software, visual gaming, physics, and signal processing.
Web development hardly requires any knowledge of linear algebra. Building strong backends to web frontends requires no knowledge of linear algebra (in most cases, randomization can achieve good load balancing if you are building backend farms).
Another application is in computer graphics. Using very simple linear algebra, as well as parts of other branches of mathematics, you can easily make objects move around in a virtual world, make them larger or smaller.


















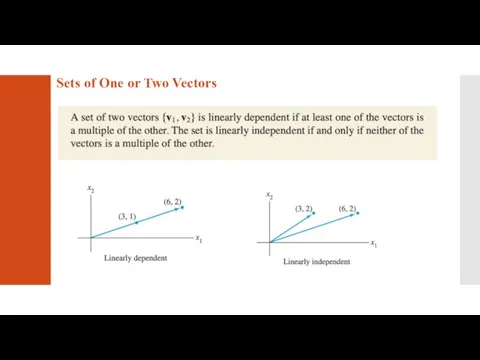

 Параллельные прямые
Параллельные прямые Вариационные ряды и их характеристики. Глава 3. Элементы математической статистики
Вариационные ряды и их характеристики. Глава 3. Элементы математической статистики Геометричне моделювання організаційних кластерних сруктур
Геометричне моделювання організаційних кластерних сруктур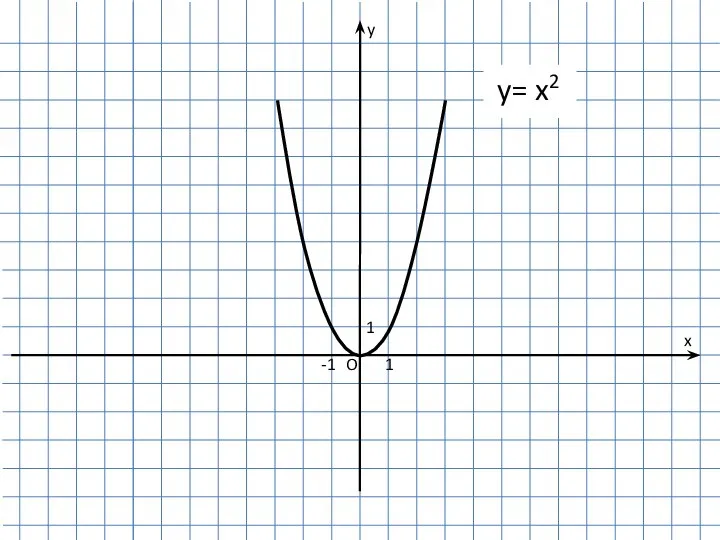 Преобразование графиков функции
Преобразование графиков функции Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Открой свою звезду. Математический диктант
Открой свою звезду. Математический диктант Операции над множествами
Операции над множествами Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности
Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности Десятки. Мозаика заданий
Десятки. Мозаика заданий Переместительное свойство умножения
Переместительное свойство умножения Погрешность прямых измерений
Погрешность прямых измерений Математический анализ. Неопределенный интеграл
Математический анализ. Неопределенный интеграл Планиметрия. Задачи
Планиметрия. Задачи Формулы приведения
Формулы приведения Elemente de teoria reziduurilor
Elemente de teoria reziduurilor Математика в медицине
Математика в медицине Таблица для мешка по двум признакам
Таблица для мешка по двум признакам Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел
Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел  Волшебная страна - Геометрия
Волшебная страна - Геометрия угол между прямой и плоскостью (1)
угол между прямой и плоскостью (1) Решение задачи Корабли или история 7 семестров
Решение задачи Корабли или история 7 семестров Деление окружности на равные части
Деление окружности на равные части Психогеометрия
Психогеометрия Показательная функция
Показательная функция Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Медианы, биссектрисы и высота треугольника
Медианы, биссектрисы и высота треугольника Математическая викторина
Математическая викторина Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей