Содержание
- 2. Последовательность Что такое последовательность? Признаки последовательности: Элементы последовательности располагаются строго в определённом порядке. Каждому члену последовательности
- 3. Числовая последовательность
- 4. Примеры числовых последовательностей 1, 2, 3, 4, 5, … - ряд натуральных чисел; 2, 4, 6,
- 5. Словесный способ. Правила задания последовательности описываются словами, без указания формул (часто когда нет закономерности между элементами
- 6. 2. Аналитический способ. Любой n-й элемент последовательности можно определить с помощью формулы. Пример 1. Последовательность четных
- 7. 3. Рекуррентный способ. Указывается правило, позволяющее вычислить n-й элемент последовательности, если известен ее предыдущий элемент.
- 8. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… Числа
- 9. Возрастание числовой последовательности Последовательность {уn} называют возрастающей последовательностью, если каждый ее член больше предыдущего: у1 Пример:
- 10. Убывание последовательности Последовательность {уn} называют убывающей последовательностью, если каждый ее член меньше предыдущего: у1 > y2
- 11. Последовательность (уn), называют ограниченной сверху, если все ее члены не больше некоторого числа. Последовательность (уn) ограничена
- 12. Последовательность (уn), называют ограниченной снизу, если все ее члены не меньше некоторого числа. Последовательность (уn) ограничена
- 13. Если последовательность ограничена и снизу и сверху, то ее называют ограниченной последовательностью. Ограниченность последовательности означает, что
- 15. Скачать презентацию












 Uravnenia_i_neravenstva_Sistemy_uravneniy
Uravnenia_i_neravenstva_Sistemy_uravneniy Трапеция
Трапеция Турнир имени Лоповка
Турнир имени Лоповка Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  График квадратичной функции, содержащей переменную под знаком абсолютной величины
График квадратичной функции, содержащей переменную под знаком абсолютной величины Учебно-методический комплект по математике по ФГОС второй ступени
Учебно-методический комплект по математике по ФГОС второй ступени Введение в геометрию
Введение в геометрию Треугольник паскаля
Треугольник паскаля Пперпендикулярные прямые
Пперпендикулярные прямые Начертательная геометрия – это не просто, это очень просто
Начертательная геометрия – это не просто, это очень просто Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс
Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Тела и поверхности вращения
Тела и поверхности вращения Интерактивная игра-тренажёр. Сколько? Соотношение числа и цифры
Интерактивная игра-тренажёр. Сколько? Соотношение числа и цифры Вписанные и описанные четырехугольники
Вписанные и описанные четырехугольники Дифференциальные уравнения
Дифференциальные уравнения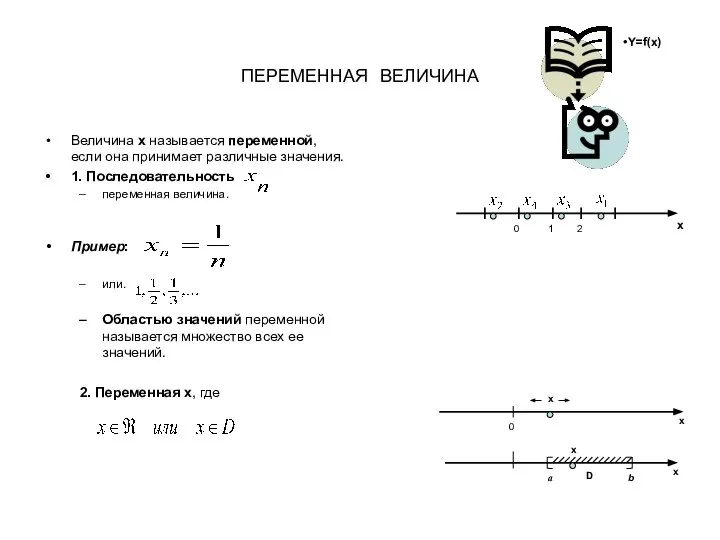 Понятие функции, предел
Понятие функции, предел Движения. 9-й класс
Движения. 9-й класс Окружность и круг. Задачи
Окружность и круг. Задачи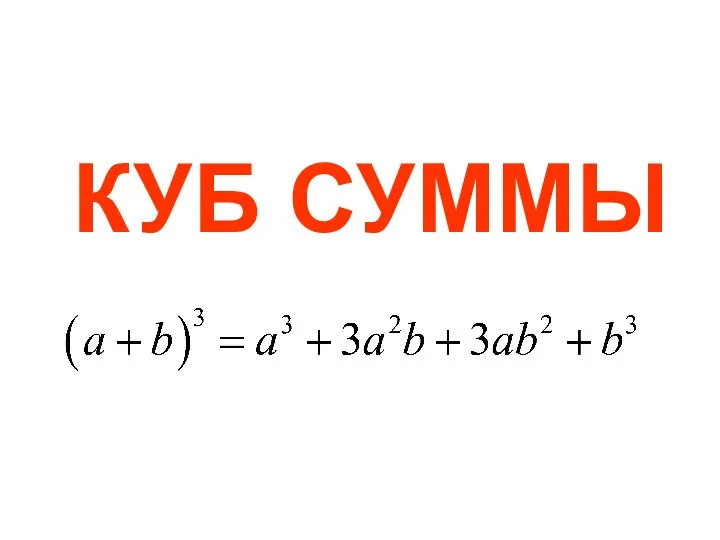 Куб суммы
Куб суммы Презентация на тему Комбинаторные задачи: размещения
Презентация на тему Комбинаторные задачи: размещения  Схемы к задачам
Схемы к задачам Функция у-сосх, её свойства и график
Функция у-сосх, её свойства и график Простейшие тригонометрические уравнения. Задания для устного счета
Простейшие тригонометрические уравнения. Задания для устного счета Отображения (функции)
Отображения (функции) Различные виды тестирования при изучении темы Десятичные дроби
Различные виды тестирования при изучении темы Десятичные дроби Логарифмы вокруг нас
Логарифмы вокруг нас Прикладная математика. Системы уравнений
Прикладная математика. Системы уравнений