Геометрические решения тригонометрических задач

«АРИФМЕТИЧЕСКИЕ ЗНАКИ – ЭТО ЗАПИСАННЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ, А ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ – ЭТО НАРИСОВАННЫЕ ФОРМУЛЫ.»
Д. ГИЛБЕРТ

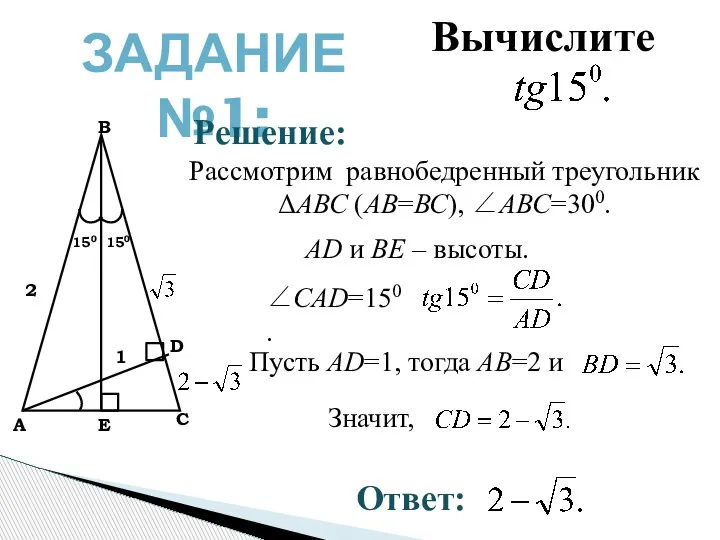
ЗАДАНИЕ №1:
В
А
С
D
E
2
1
150
150
Рассмотрим равнобедренный треугольник ΔАВС (АВ=ВС), ∠АВС=300.
AD и ВЕ – высоты.
∠САD=150.
Пусть AD=1, тогда АВ=2 и
Значит,
Ответ:
Вычислите
Решение:

А
С
В
1
1
D
450
ЗАДАНИЕ №2:
Вычислите
Рассмотрим равнобедренный треугольник ΔАВС (АВ=ВС), ∠АВС=450.
Так как ∠ВСА=67030’, то ∠CAD=22030’.
Пусть AD=1,
Ответ:
Решение:

ЗАДАНИЕ №3:
Докажите тождество
А
В
D
С
x
x
2x
3x
x
2x
Рассмотрим равнобедренный треугольник ΔАВС (АВ=ВС), точку D (D∈BC и AD=BD=AC).
Доказательство:
Пусть ∠АВС=х, тогда ∠BAD=x, ∠ADC=2x, ∠ACD=2x ∠DAC=x, ∠ADB=3x.
Суммы внутренних углов треугольников ABD, ACD и АВС равны по 5х, т.е. х=360.
Итак, ∠АВС=360 и ∠ADC=720.
Так как D∈BC, то ВС=BD+DC.
Пусть BD=1, тогда АВ=2cos360 и CD=2cos720.
Так как АВ=ВС,
то 2cos360=1+2cos720.
Значит,

ЗАДАНИЕ №4:
Докажите тождество
А
В
D
С
x
2x
2x
5x
x
3x
Так как треугольники ABD, ADC и ABC равнобедренные, то 7х=1800,
т.е.
Доказательство:
2. BC = BD + DC.

Пусть длина общей высоты, проведенной из вершины А в треугольниках ABD, ADC и ABC, равна 1 (H∈BC, AH⊥BC, AH=1), то:
из ΔABH (AH⊥BH)
из ΔADH (AH⊥DH)
Значит,
из ΔAСH (AH⊥СH)

ЗАДАНИЕ №5:
Вычислите
А
В
С
D
Решение:
В задаче 3 были определены величины углов с вершинами в точках A, B, C и D.
ΔАВС ~ ΔCAD, так как оба они равнобедренные с общим углом при основаниях (∠АСВ=∠ACD).
Значит,
Если АС=а и АВ=b (a
Отсюда
Это число называют золотым сечением или числом Фидия (Фидий – отец Архимеда).
Так как sin 180 = cos 720, а cos 720 = ,
то sin 180 =
Ответ:

ЗАДАНИЕ №6:
Вычислите
В
А
С
D
E
1
100
Решение:
Рассмотрим прямоугольный треугольник ΔАВС, в котором ∠АВС=100, ∠АСВ=900, D∈BC, E∈AB и AD=DE=BE.
Пусть АС=1.
Определив величины углов, замечаем:
ВС= ctg100, BD=4cos100, CD=tg600.
Так как ВС=BD+DC, то ctg100=4cos100+tg600.
Ответ:

В
А
С
D
E
1
α
ЗАДАНИЕ №7:
α
α
Докажите, что sin 2α=2 sin α cos α
Рассмотрим равнобедренный треугольник ΔАВС (АВ=ВС=1), ∠АВС=2α, AD и ВЕ – высоты.
По рисунку AD=sin 2α, AE=EC=sin α, BE=cos α.
Так как ΔABE ~ ΔCAD, то
Доказательство:
Значит, sin 2α=2 sin α cos α.
①

В
С
D
E
1
α
α
α
②
Доказательство:
Докажите, что 1 – cos2α = 2 sin2α
AE=EC=sin α, BD=cos 2α, CD = 1-cos 2α
ΔABE ~ ΔCAD
Тогда, , т.е.
Значит, 1 – cos2α = 2 sin2α

ЗАДАНИЕ №8:
А
С
В
c
h
a
α
β
Докажите, что
sin (α+β) = sin α cos β + cos α sin β
Доказательство:
Рассмотрим ΔАВС, в котором BD⊥AC, ∠ABD=α, ∠CBD=β. Точка D – внутренняя точка отрезка АС, так как по условию α и β – острые углы. Пусть ВС=а, АС=b, АВ=с и BD=h.
D

ЗАДАНИЕ №9:
Каким должен быть
острый угол х, если
x
A
C
B
D
❶
Рассмотрим рисунок ❶
Решение:
по теореме косинусов,
а АВ=4 по теореме Пифагора.
Значит, D∈AB.

❷
x
A
C
B
D
Так как ΔАВС прямоугольный и
По теореме косинусов из ΔACD следует, что
где буквой у обозначена длина стороны AD.
Ответ: 600.
то в Δ ACD ∠ADC=900.
Тогда x=600.

ЗАДАНИЕ №10:
Вычислите arctg 1 + arctg 2 + arctg 3.
arctg 3 = ∠BAM,
arctg 2 = ∠CAN,
arctg 1 = ∠BAC
(∠BAC – острый угол прямоугольного равнобедренного треугольника АВС).
Решение:
Итак, arctg 1 + arctg 2 + arctg 3 = π.

ЗАДАНИЕ №11:
Решение:
Вычислите
A
В
С
D
Ответ:

ЗАДАНИЕ №12:
Решение:
Вычислите
cos (arcctg 3 + arctg 0,5).
D
ctg ∠DAB=3 и tg ∠DAC=0,5.
ΔАВС – равнобедренный, ∠АВС=900.
Значит,
Ответ:

ЗАДАНИЕ №13:
Решение:
Вычислите
D
Так как
то можно считать, что
- это угол прямоугольного треугольника, у которого отношение катетов равно 1 : 2. Тогда величину этого угла можно рассматривать как arctg 2. Аналогично рассуждая, получим
Далее, по рисунку ∠МАВ=arctg3 и ∠NAC=arctg 2, а их сумма равна
Итак,