Статистическое изучение динамики общественных явлений. Лекция №8

01
02
03
Правила построения рядов динамики
Аналитические показатели ряда динамики
ВОПРОСЫ
04
05
Понятие о статистических рядах динамики
Средние показатели ряда динамики
04
05
Методы анализа основной тенденции ряда динамики
06
Методы изучения сезонных колебаний

Вопрос 1. Понятие о статистических рядах динамики
Рядами динамики являются статистические данные, отображающие развитие явления во времени.
Ряд динамики состоит из;
1) показателей времени t (определенные даты (моменты) времени либо отдельные периоды (годы, кварталы, месяцы, сутки));
2) показателей уровня изучаемого явления у (относятся к конкретным показателям времени и отображают количественную оценку (меру) развития изучаемого явления во времени, могут выражаться абсолютными, относительными и средними величинами).

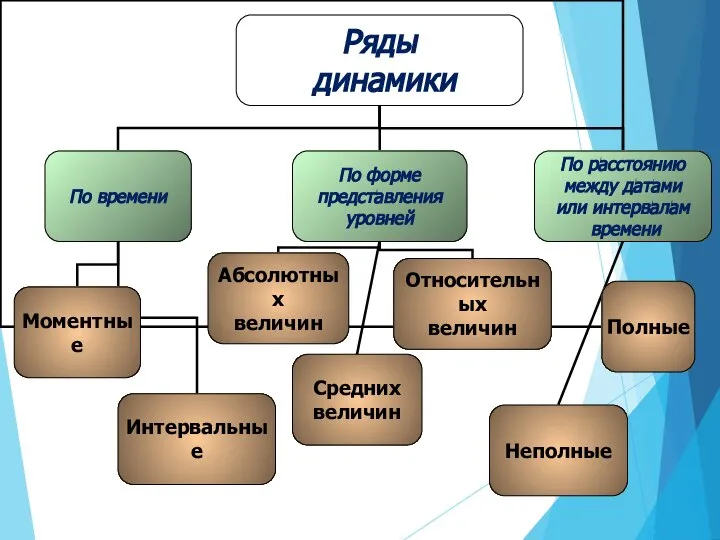
В зависимости от характера изучаемого явления различают моментные и интервальные ряды динамики. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики может служить информация о списочной численности работников предприятия.
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности.

Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы времени).
Примером интервального ряда динамики могут служить данные о производстве продукции.

Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени.
Например, суммируя объем производства за три месяца получают его объем за квартал. Суммирование уровней за последовательные интервалы времени позволяет получать ряды динамики более крупных периодов.

В статистике широко используются интервальные ряды динамики с нарастающими итогами. Их применение обусловлено потребностями отображения изменения изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней.

С помощью рядов динамики изучение законо-мерностей развития социально-экономических явле-ний осуществляется в следующих основных направ-лениях:
– характеристика уровней изучаемых явлений;
– измерение динамики изучаемых явлений посред-ством расчета статистических показателей;
– выявление и количественная оценка основной тен-денции ряда динамики (определение тренда);
– изучение сезонных колебаний;
– экстраполяция и прогнозирование.

Вопрос 2. Правила построения рядов динамики
Необходимым условием получения правильных выводов при анализе рядов динамики является сопоставимость уровней ряда между собой. Статистические данные должны быть сопоставимы:
1) по территории (соблюдение одних и тех же территориальных границ);
2) по кругу охватываемых объектов (сравнение совокупнстей с равным числом элемнтом);

3) по времени регистрации (равенство периодов времени, за которые приводятся данные (для интервального ряда) или представление показателей на одну и ту же дату (для моментных рядов динамики)
4) по методологии расчета (использование единой методологии расчета);
5) по единицам измерения (использование одних и тех же единиц измерения);
6) по ценам (использование постоянных или сопоставимых цен).
Возможными являются и другие причины несопоставимости.

В ряде случаев несопоставимые данные могут быть приведены к сопоставимому виду путем дополнительных расчетов. В частности, в статистике применяется прием, известный как смыкание рядов динамики.
Этот прием позволяет преодолеть несопоставимость данных, возникающую вследствие изменения во времени территориальных границ, круга охватываемых объектов или методологии расчета показателей, и получить единый ряд сопоставимых данных за весь период времени.

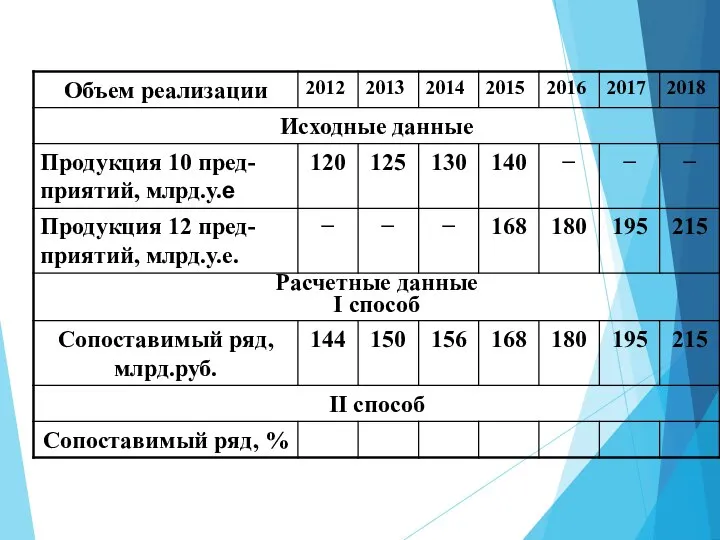
Пример. Имеются данные об объеме реализации продукции производственного объединения, в которое входило: с 2012 г. по 2015 г. - 10 предприятий;
с 2015 г. – 12 предприятий.
Требуется получить единый ряд, который был бы пригоден для характеристики динамики объема реализации продукции за весь рассматриваемый период.

Решение
Рассчитываем коэффициент смыкания по данным за 2015 г.:
Уровни 2012–2014 гг. корректируем на коэффициент смыкания:
2012 г. 120 х 1,2=144 млрд. руб.
2013 г. 125 х 1,2 = 150 млрд. руб.
2014 г. 130 х 1,2 = 156 млрд. руб.
В результате получается ряд сопоставимых абсолютных величин.

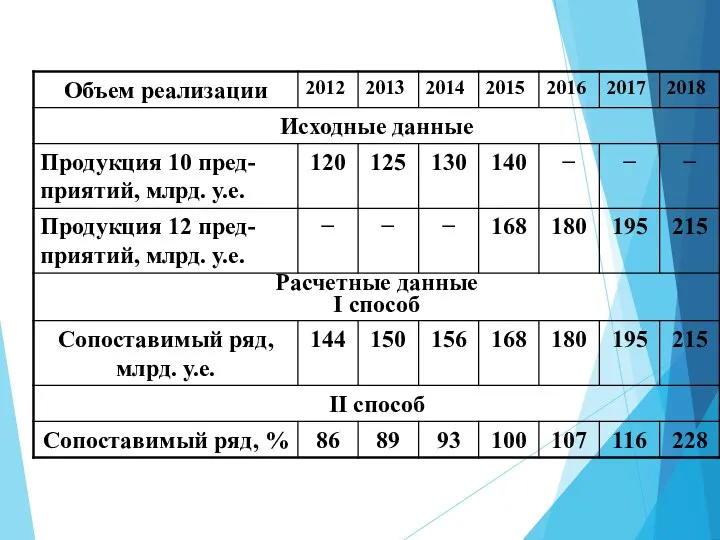
Другой способ смыкания рядов динамики заключается в том, что уровни года, в котором произошли изменения (в нашем случае 2015 г.) принимаются за 100%, а остальные пересчитываются в процентах по отношению к ним. В результате получается ряд сопоставимых относительных величин (в %).

Проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных объектов. В таких случаях ряды динамики приводятся к общему основанию, т. е. к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения (100%), а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.

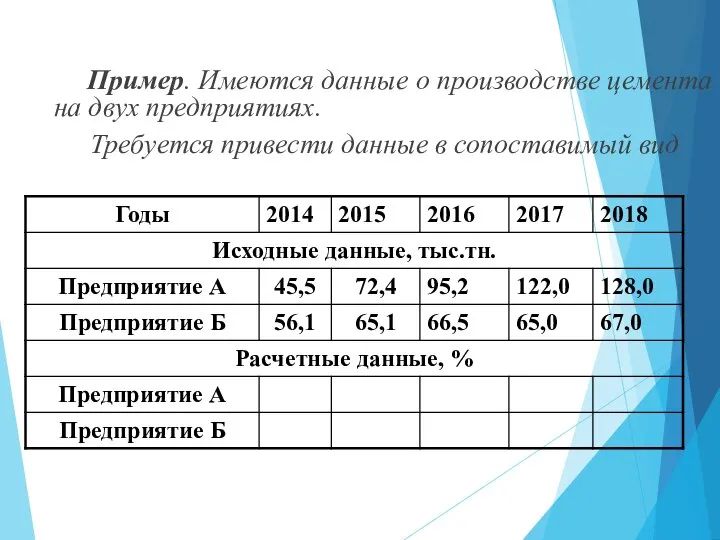
Пример. Имеются данные о производстве цемента на двух предприятиях.
Требуется привести данные в сопоставимый вид

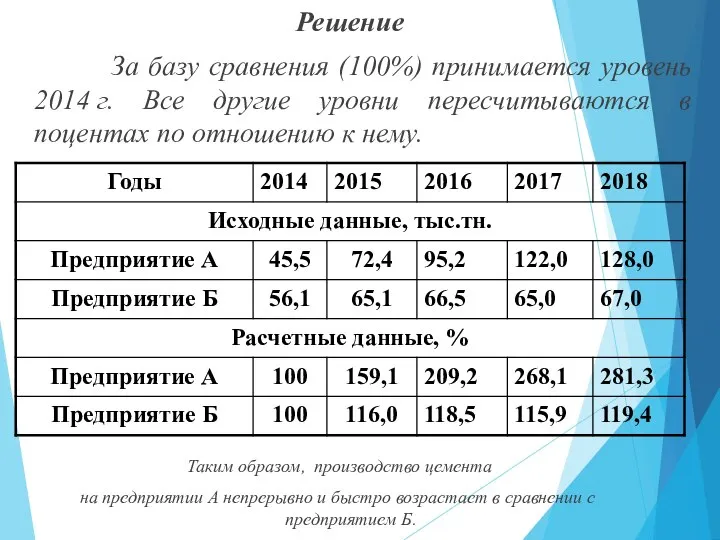
Решение
За базу сравнения (100%) принимается уровень 2014 г. Все другие уровни пересчитываются в поцентах по отношению к нему.
Таким образом, производство цемента
на предприятии А непрерывно и быстро возрастает в сравнении с предприятием Б.

Вопрос 3. Аналитические показатели
ряда динамики
При изучении динамики явлений или процессов возникает проблема описания интенсивности происходящих изменений. Анализ интенсивности изменения явлений во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней ряда динамики. К ним относятся:
1) абсолютный прирост;
2) темп (коэффициент) роста;
3) темп (коэффициент) прироста;
4) абсолютное значение одного процента прироста.

Показатели анализа динамики могут вычисляться:
а) с постоянной базой сравнения;
б) с переменной базой сравнения.
При этом принято называть:
- сравниваемый уровень отчетным;
- уровень, с которым производится сравнение, – базисным.

При расчете показателей динамики с постоянной базой, каждый уровень сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.В качестве базисного уровня выбирается:
а) начальный уровень ряда динамики;
б) уровень, с которого начинается новый этап развития явления.
При расчете показателей динамики с переменной базой каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели называются цепными.

Абсолютный прирост характеризует абсолютное увеличение (уменьшение) уровня ряда за определенный промежуток времени.
Абсолютный прирост цепной
Δyцi = yi –yi-1
где yi – отчетный уровень i-го периода;
yi-1 –уровень предшествующего периода.
Абсолютный прирост базисный
Δyбi=yi – yб
где yб – уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой следующим соотношением: сумма последовательных цепных абсолютных приростов равна базисному приросту за весь промежуток времени:

Пример. Выпуск продукции фирмы «А» составил:
2016 г. – 160 млрд. у.е.;
2017 г. – 200 млрд. у.е.;
2018 г. – 252 млрд. у.е.
Требуется рассчитать все возможные показатели динамики.

Цепной абсолютный прирост
в 2017 г. по сравнению с 2016 г.
∆у2017/2016 = 200 − 160 = 40 млрд. у.е.
в 2018 г. по сравнению с 2017 г.
∆у2018/2017 =252 − 200= 52 млрд. у.е.
Базисный абсолютный прирост
в 2018 г. (за базисный уровень принимается начальный уровень ряда - 2016 г.)
∆у2018/2016 = 252 − 160 = 92 млрд у.е.
При этом сохраняется соотношение между цепными и базисным абсолютными приростами:
∆у2018/2016 = ∆у2017/2016 + ∆у2018/2017
40+52=92 млрд у.е.

Коэффициент роста показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение. Коэффициент роста, выраженный в процентах, называется темпом роста.
Темп (коэффициент) роста цепной:
Темп (коэффициент) роста базисный:

Между цепными и базисными коэффициентами роста существует взаимосвязь:
а) произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период
б) частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста

По данным нашего примера
Цепной темп роста
в 2017 г. по сравнению с 2016 г.
200/160 · 100= 125%
в 2018 г. по сравнению с 2017 г. − 126% 252/200 ·100 = 126 %
Базисный темп роста
в 2018 г. по сравнению с 2016 г.
252/160 · 100=157,5%
При этом сохраняется соотношение между цепными и базисными коэффициентами роста:
1,25 ·1,26 = 1,575

Показатели темпа или коэффициента прироста дают относительную оценку скорости изменения уровня ряда в единицу времени. Темп прироста показывает, на сколько процентов сравниваемый уровень больше уровня, принятого за базу сравнения.
Темп (коэффициент) прироста цепной:
Темп прироста можно получить также путем вычитания из темпа (коэффициента) роста 100% или 1.
ТПР = ТР − 100%, КПР = КР − 1.

Темп (коэффициент) прироста базисный:

В нашем примере
Цепной темп прироста
в 2017 г. по сравнению с 2016 г.
40/160 · 100 = 25% либо 125% −100%=25%
в 2018 г. по сравнению с 2017 г.
52/200 · 100=26% либо 126% − 100=26%
Базисный темп прироста
в 2018 г. по сравнению с 2016 г.
92/160 ∙ 100=57,5% либо 157,5% − 100=57,5%

Абсолютное значение одного процента прироста определяется как результат деления абсолютного прироста на темп прироста за тот же период времени.
По данным нашего примера
Абсолютное значение одного процента прироста в 2017 г. составило 1,6 млрд. у.е. (40/25), в 2018 г. − 2 млрд. у.е. В целом за период − 1,6 млрд. у.е. (92/57,5).

Помимо перечисленных показателей в ряде случаев рассчитываются так называемые процентные пункты роста, которые представляют собой разность базисных темпов роста двух смежных периодов.
В нашем примере в 2018 г. по сравнению с 2017 г. темп роста выпуска продукции увеличился на 32,5 пункта (157,5 − 125).
В отличие от темпов роста, пункты роста можно суммировать. Результат суммирования последовательных показателей за весь период дает базисный темп прироста.

4. Средние показатели ряда динамики
Обобщающая характеристика динамики исследуемого явления определяется при помощи следующих средних показателей:
─ средний уровень ряда;
─ средний абсолютный прирост
─ средний темп роста;
─ средний темп прироста.

Для интервальных рядов динамики средний уровень ряда определяется:
а) при равных интервалах по формуле средней арифметической простой:
где у1,…, уn – абсолютные уровни ряда;
n – число уровней.
Например, требуется определить средний уровень интервального ряда динамики (см. вопрос 1):

б) при неравных интервалах по формуле средней арифметической взвешенной
где t –длительность интервалов времени между уровнями ряда.

Средний уровень моментных рядов динамики определяется:
а) для ряда с равноотстоящими датами по формуле средней хронологической простой:

Например, требуется определить средний уровень приведенного моментного ряда динамики (см. вопрос 1):

б) для ряда с неравноотстоящими датами по формуле средней хронологической взвешенной:

Средний абсолютный прирост рассчитывается двумя способами:
а) цепным (исходя из цепных абсолютных приростов):
где m – число абсолютных приростов (m=n–1, n – число членов ряда);
б) базисным (исходя из общего базисного абсолютного прироста):

Для моментного ряда динамики (см. вопрос 1)средний абсолютный прирост, рассчитанный цепным способом, составляет 2 чел.:
Расчет базисным способом дает тот же результат Таким образом, средний абсолютный ежеквартальный прирост численности составляет 2 чел.

Средний коэффициент роста для рядов с равными интервалами, или с равноотстоящими датами, рассчитывается:
а) цепным способом (по формуле средней геометрической):
где m – число коэффициентов роста (m=n–1);
б) базисным способом:

Средний темп роста для рядов с равными интервалами, или равноотстоящими датами, рассчитывается по формуле:
Средний коэффициент роста для моментного ряда (см. вопрос 1) составляет 1,0103 , т. е. средний ежеквартальный рост численности составляет 101, 3 %.

Средние темпы (коэффициенты) прироста рассчитываются на основе средних темпов или коэффициентов роста посредством вычитания из последних 100% или 1:
Средний темп прироста для нашего примера составляет 1,03% (101,03% – 100,00%).

При одновременном анализе динамики двух явлений представляет интерес сравнение интенсивности изменения их во времени. Такое сопоставление производится:
1) при наличии динамических рядов одинакового содержания, но относящихся к различным территориям или объектам;
2) при сравнении рядов разного содержания, характеризующих один и тот же объект.

Сравнение интенсивности изменений уровней рядов во времени возможно с помощью коэффициентов опережения, представляющих собой отношение базисных темпов роста или прироста двух рядов динамики за одинаковые отрезки времени:

Например, темп роста объемов производства на предприятии в отчетном году составил 126%, а темп роста численности – 120%.
Таким образом, темп роста объемов производства в отчетном году опережал рост численности на предприятии в 1,05 раза (126/120).

Коэффициент опережения может быть исчислен также на основе сравнения средних темпов роста или темпов прироста:

Вопрос 5. Методы анализа основной тенденции ряда динамики
Основной тенденцией ряда динамики (или трендом) называется устойчивое изменение уровня явления во времени, обусловленное влиянием постоянно действующих факторов и свободное от случайных колебаний.
В случаях, когда уровни динамического ряда непрерывно растут или непрерывно снижаются, основная тенденция ряда является очевидной. Однако достаточно часто уровни динамических рядов претерпевают различные изменения (т. е. то растут, то убывают), и общая тенденция неясна. Задача статистики заключается в выявлении тенденции в таких рядах. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Метод укрупнения интервалов является наиболее простым. Он основан на увеличении периодов времени, к которым относятся уровни ряда динамики. Одновременно уменьшается количество интервалов.

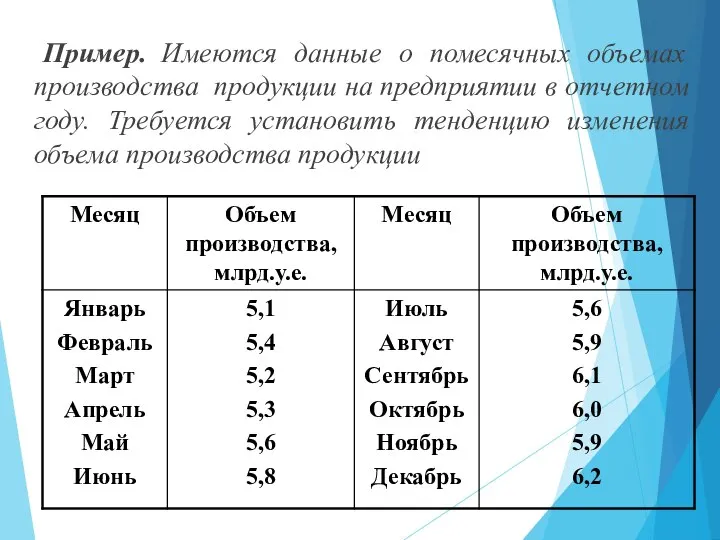
Пример. Имеются данные о помесячных объемах производства продукции на предприятии в отчетном году. Требуется установить тенденцию изменения объема производства продукции

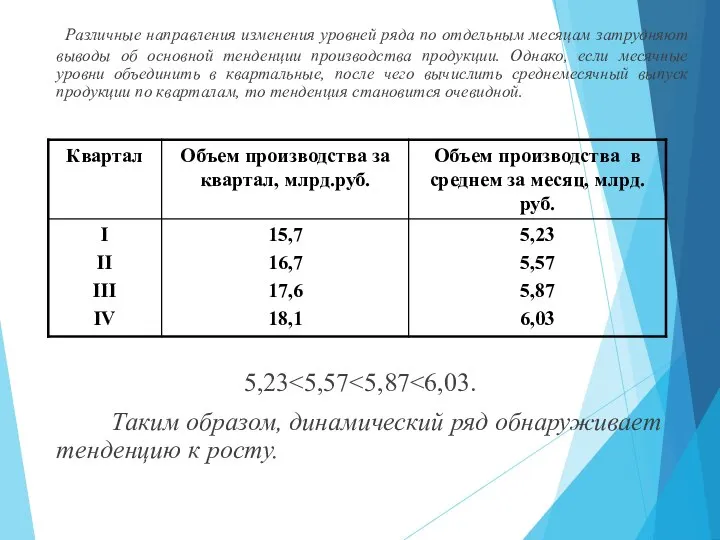
Различные направления изменения уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства продукции. Однако, если месячные уровни объединить в квартальные, после чего вычислить среднемесячный выпуск продукции по кварталам, то тенденция становится очевидной.
5,23<5,57<5,87<6,03.
Таким образом, динамический ряд обнаруживает тенденцию к росту.

Метод скользящей средней заключается в следующем. Определяется средний уровень из определенного объема нечетного числа первых по счету уровней ряда, а затем из такого же числа уровней, но начиная со вто-рого по счету. Затем с третьего и так далее. Таким образом, средняя скользит по ряду ди-намики, передвигаясь на один уровень.
Пример. Имеются данные об данных о динамике производительности труда на предприятии. Требуется установить тенденцию изменения объема производства продукции

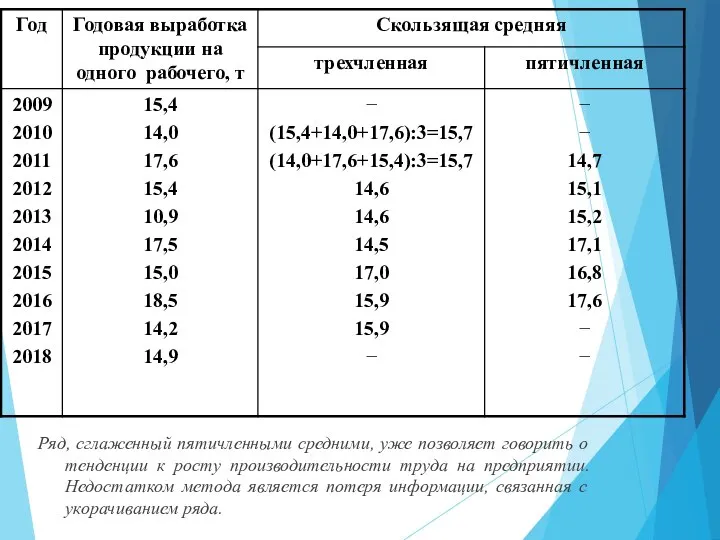
Ряд, сглаженный пятичленными средними, уже позволяет говорить о тенденции к росту производительности труда на предприятии. Недостатком метода является потеря информации, связанная с укорачиванием ряда.

Рассмотренные методы дают возможность опре-делить общую тенденцию изменения уровней ряда динамики. Однако они не позволяют получить обобщенную статистическую модель тренда. С этой целью применяют метод аналитического вырав-нивания рядов динамики. Основным содержанием метода является то, что общая тенденция развития представляется как функция времени:
ŷ = f(t),
где ŷ – уровень динамического ряда, вычислен-ный по соответствующему уравнению на момент времени t.

Определение теоретических уровней ряда динамики производится на основе так называемой адекватной мате-матической модели, наилучшим образом отображающей основную тенденцию. Простейшими моделями для ото-бражения социально-экономических процессов являются следующие:
линейная ŷ = а0 + а1t
показательная ŷ =
степенная ŷ = а0 а1t
парабола ŷ = а0 + а1t + а2t2

Расчет параметров функции обычно производится методом наименьших квадратов. Σ(ŷ–y)2→min
Параметры уравнения, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе полученного уравнения тренда вычисляются теоретические уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней у плавно изменяющимися теоретическими уровнями.
Для окончательного выбора вида адекватной математической функции используются специальные критерии математической статистики (критерий χ2, Колмогорова – Смирнова и другие).

Вопрос 6.
Методы изучения сезонных колебаний
При сравнении квартальных и месячных данных многих социально-экономических явлений зачастую обнаруживаются периодические колебания, возникающие под влиянием смены времени года. Они являются результатом влияния природно-климатических условий, общеэкономических факторов, а также других многочисленных и разнообразных факторов, которые часто являются регулируемыми.

В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название сезонных колебаний или сезонной волны, а динамический ряд в этом случае называется сезонным рядом динамики. Сезонные колебания наблюдаются в различных отраслях экономики, в том числе в отраслях химико-лесного комплекса. В ряде случаев они могут отрицательно влиять на результаты производственной деятельности. Поэтому встает вопрос о регулировании сезонных изменений. В основе этого регулирования должно лежать исследование сезонных колебаний.

В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой из них заключается в расчете специальных показателей, называемых индексами сезонности IS. Совокупность этих показателей отражает сезонную волну.
Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонных колебаний вычисляются по данным за несколько лет (не менее трех).

Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.
Для каждого месяца рассчитывается средняя величина уровня, например, за три года ( ), затем вычисляется среднемесячный уровень для всего ряда ( ). После этого определяются индексы сезонности, представляющие собой процентные отношения средних для каждого месяца к общему среднемесячному уровню ряда:

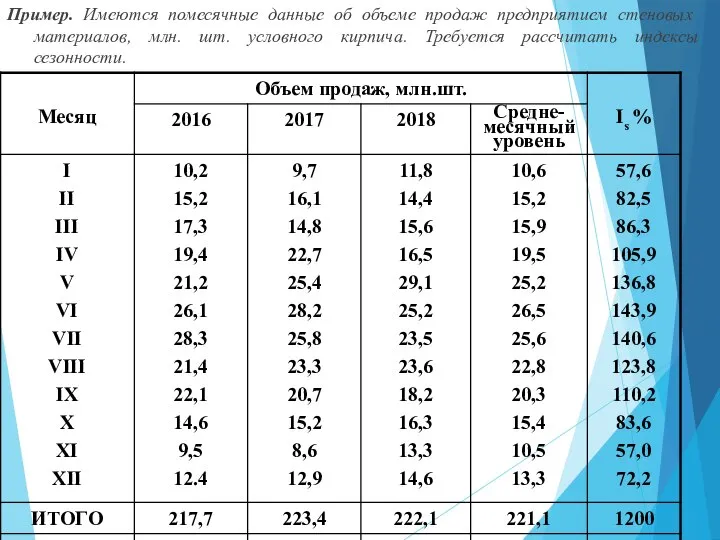
Пример. Имеются помесячные данные об объеме продаж предприятием стеновых материалов, млн. шт. условного кирпича. Требуется рассчитать индексы сезонности.

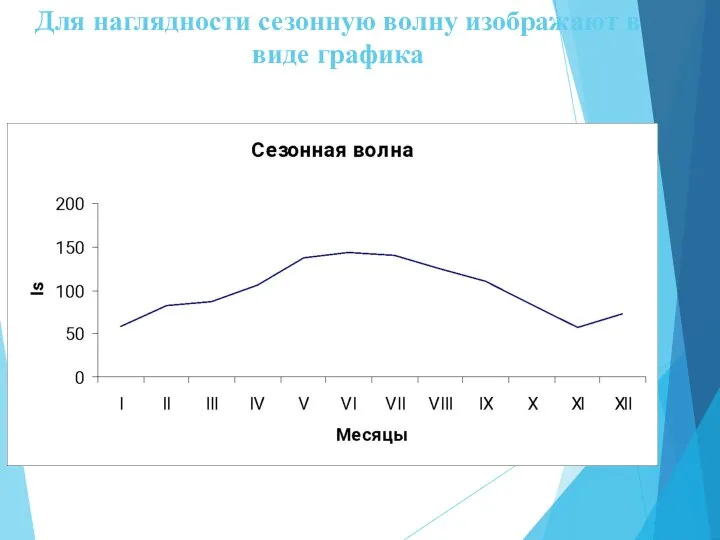
Для наглядности сезонную волну изображают в виде графика

В случае, когда уровни динамического ряда проявляют тенденцию к росту или снижению, фактические данные сопоставляются с выравненными, т. е. полученными с помощью аналитического выравнивания. Индексы сезонности рассчитываются по формуле
Имея представления о сезонных изменениях того или иного явления, предприятие может правильно распределять материальные, финансовые и трудовые ресурсы в течение года.