Гомотетия. Подобие фигур

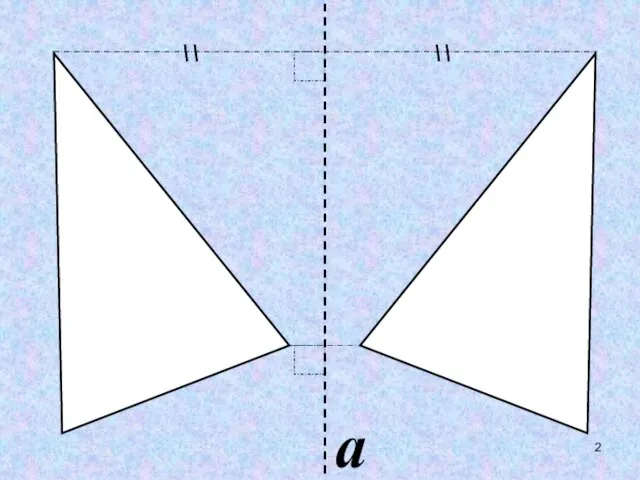
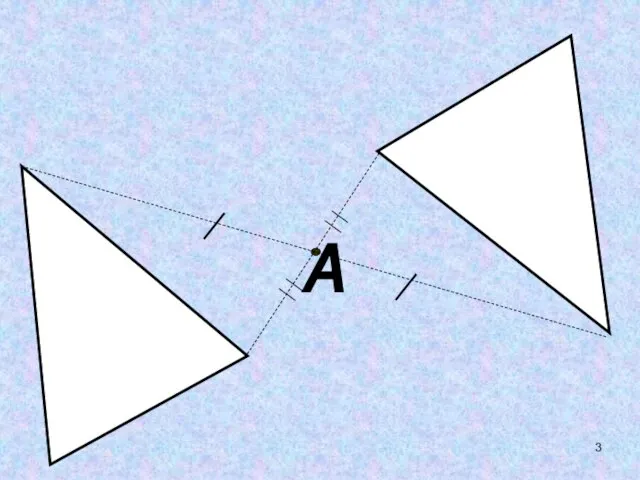
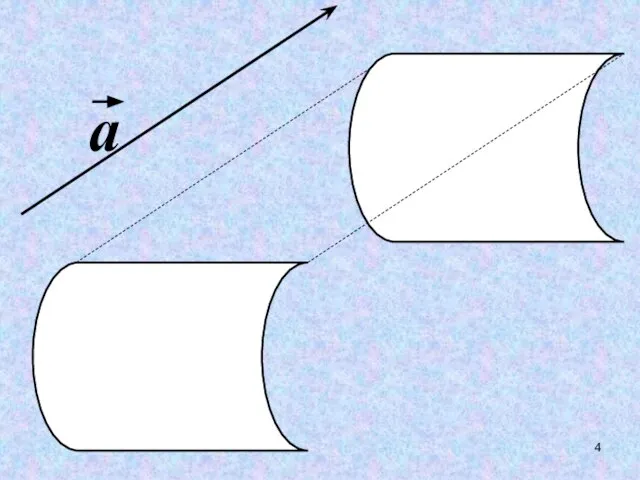
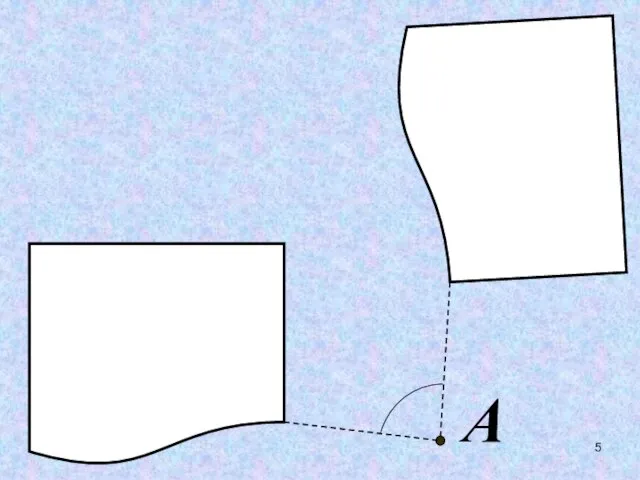
ОСЕВАЯ СИММЕТРИЯ
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
ПОВОРОТ
Д
В
И
Ж
Е
Н
И
Е

Свойства движения:
При движении прямая переходит в прямую, луч – в луч, отрезок – в отрезок.
Сохраняются расстояния между точками.
Сохраняются углы между лучами.

Следствие:
При движении фигура переходит в равную ей фигуру!!!

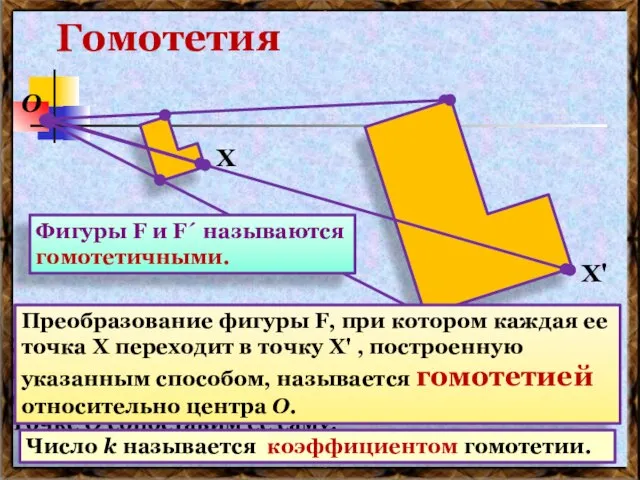
ГОМОТЕТИЯ.
Гомотетия – одно из важнейших преобразований подобия.

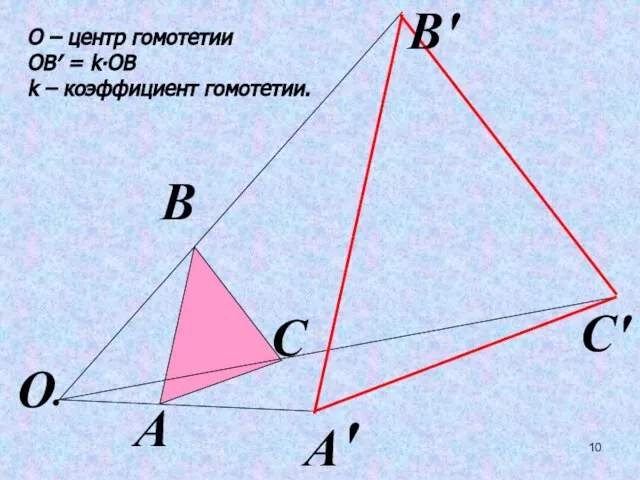
О – центр гомотетии
ОВ′ = k∙ОВ
k – коэффициент гомотетии.
О
А
А′
В
В′
С
С′

При гомотетии сохраняются только углы!!!

Рассмотрим случаи:
1 случай: k > 0
а) k > 1
б) k < 1
2 случай: k < 0

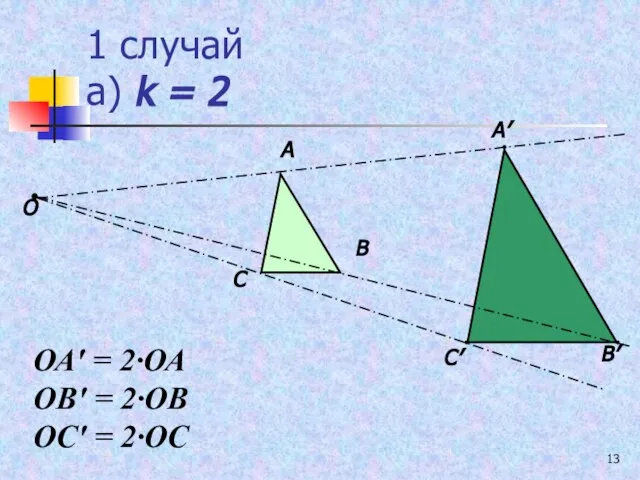
1 случай
а) k = 2
О
ОА′ = 2∙ОА
ОВ′ = 2∙ОВ
ОС′ = 2∙ОС

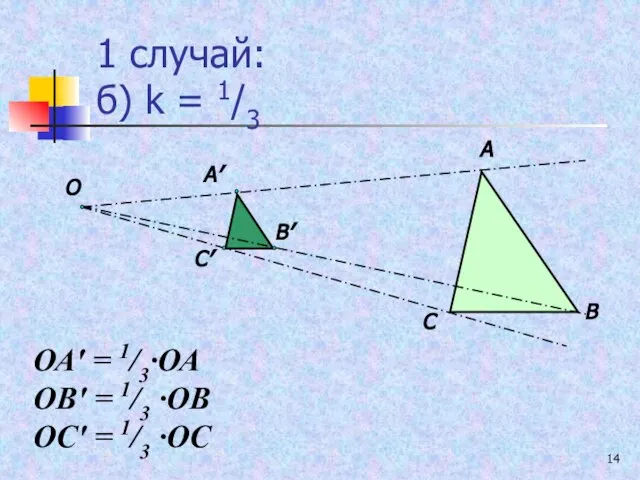
1 случай:
б) k = 1/3
А
В
С
О
А′
В′
С′
ОА′ = 1/3∙ОА
ОВ′ = 1/3 ∙ОВ
ОС′ = 1/3 ∙ОС

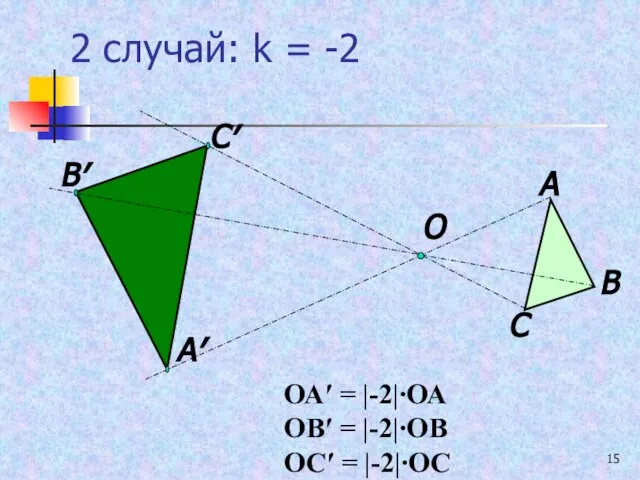
2 случай: k = -2
О
А
В
С
А′
В′
С′
ОА′ = |-2|∙ОА
ОВ′ = |-2|∙ОВ
ОС′ = |-2|∙ОС

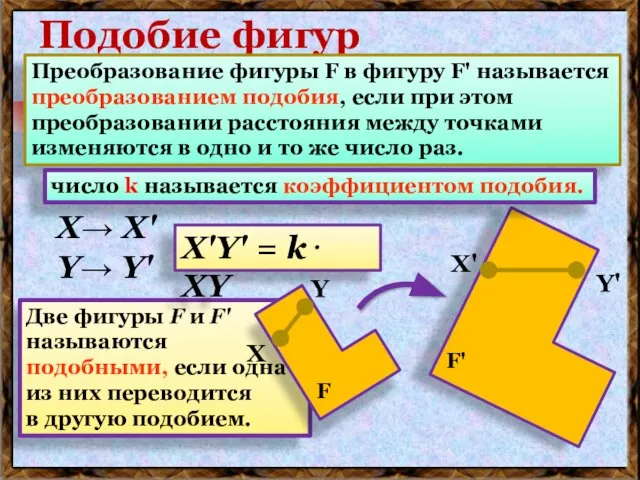
Подобие фигур
Преобразование фигуры F в фигуру F' называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз.
Две фигуры F и F' называются подобными, если одна из них переводится в другую подобием.
F
F'
Y
Х
Y'
Х'
Х→ Х'
Y→ Y'
Х'Y' = k⋅ ХY
число k называется коэффициентом подобия.

Гомотетия
Зафиксируем точку O и положительное число k. Каждой точке Х плоскости, отличной от O сопоставим точку Х' на луче OХ так, что OХ' = k ⋅ OХ. Точке O сопоставим ее саму.
O
Х
Х'
Преобразование фигуры F, при котором каждая ее точка Х переходит в точку Х' , построенную указанным способом, называется гомотетией относительно центра O.
Число k называется коэффициентом гомотетии.
Фигуры F и F´ называются гомотетичными.

В геометрии фигуры одинаковой формы принято называть подобными.

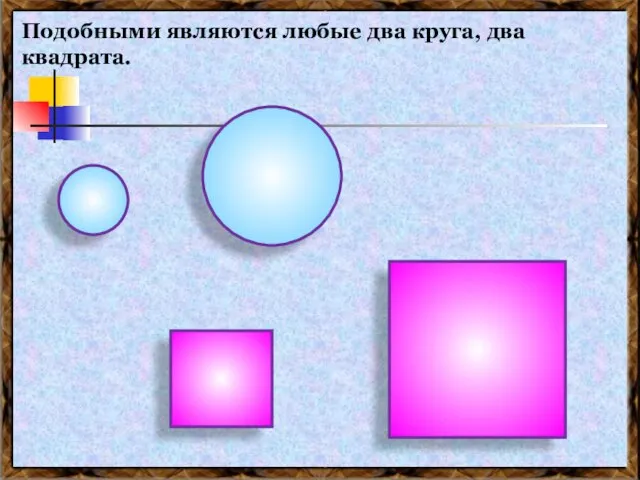
Подобными являются любые два круга, два квадрата.

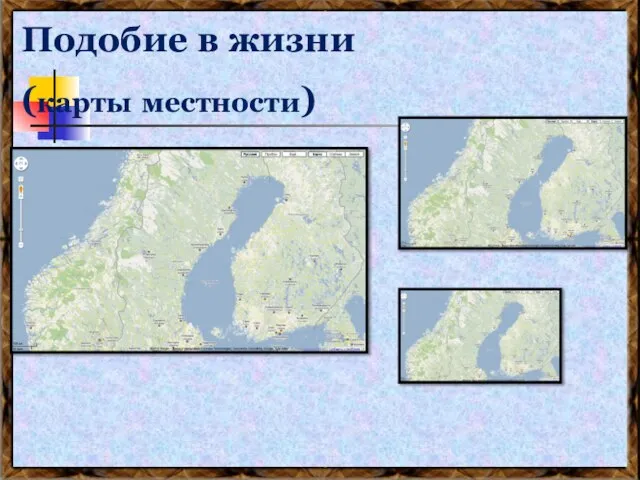
Подобие в жизни
(карты местности)

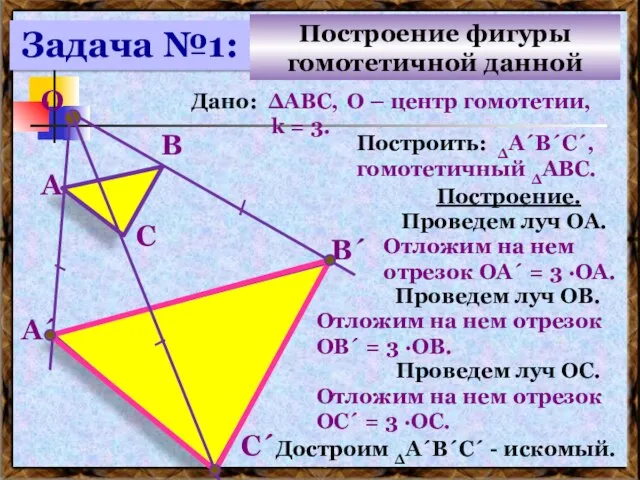
Дано: ∆АВС,
О – центр гомотетии,
k = 3.
Построить: ∆А´В´С´, гомотетичный ∆АВС.
Построение.
А
В
С´
А´
В´
С
Проведем луч ОА.
Отложим на нем отрезок ОА´ = 3 ∙ОА.
Проведем луч ОС.
Проведем луч ОВ.
Отложим на нем отрезок ОС´ = 3 ∙ОС.
Отложим на нем отрезок ОВ´ = 3 ∙ОВ.
Достроим ∆А´В´С´ - искомый.
О
Задача №1:
Построение фигуры
гомотетичной данной

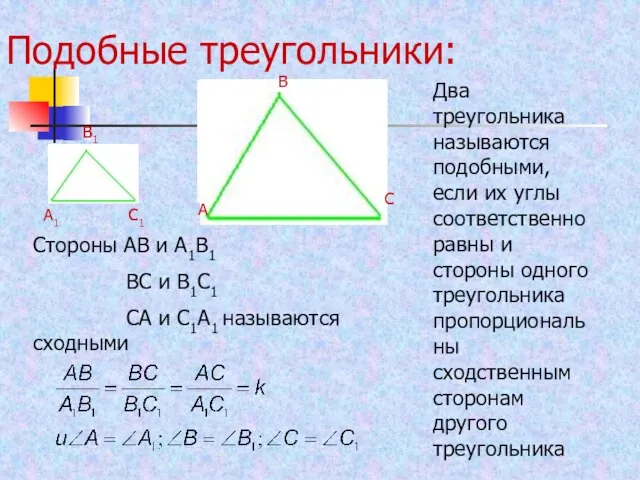
Подобные треугольники:
А
В
С
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
Стороны АВ и А1В1
ВС и В1С1
СА и С1А1 называются сходными
А1

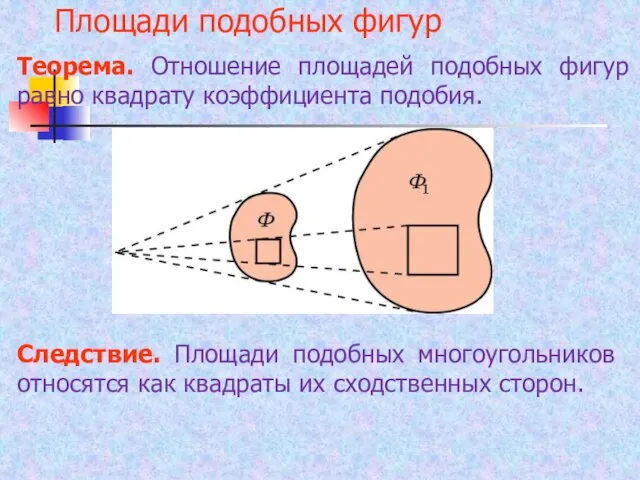
Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Следствие. Площади подобных многоугольников относятся как квадраты их сходственных сторон.

Пример 1
Периметры двух подобных многоугольников относятся как 1 : 2. Как относятся их площади?
Ответ: 1 : 4.

Пример 2
Как относятся стороны двух квадратов, если отношение площадей этих квадратов равно: а) 4 : 9; б) 3 : 4; в) 0,5 : 2?
Ответ: а) 2 : 3;
в) 1 : 2.

Пример 3
Стороны равносторонних треугольников равны 6 см и 7 см. Чему равно отношение их площадей?
Ответ: 36 : 49.

Домашнее задание:
§ 23, вопросы, № 23.2; 23.4(3)