Содержание
- 2. График одно из важных алгебраических понятий График - это линия на плоскости График один из способов
- 3. Что мы знаем о графиках? Нужны ли графики? Можно ли обойтись без умения читать график? Что
- 4. На уроках математики; В справочной литературе; График движения поездов; График изменения температур. Где в жизни вам
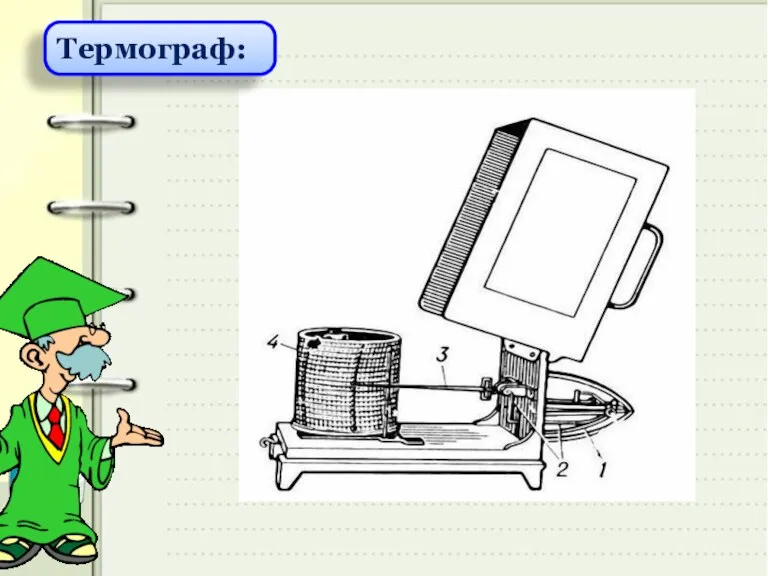
- 5. Термограф:
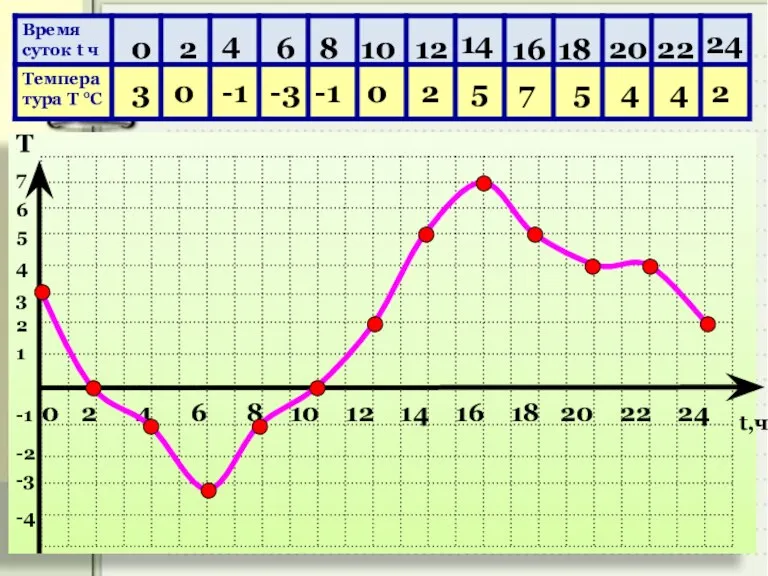
- 6. 0 3 2 0 4 -1 6 -3 8 -1 10 0 12 2 0 14
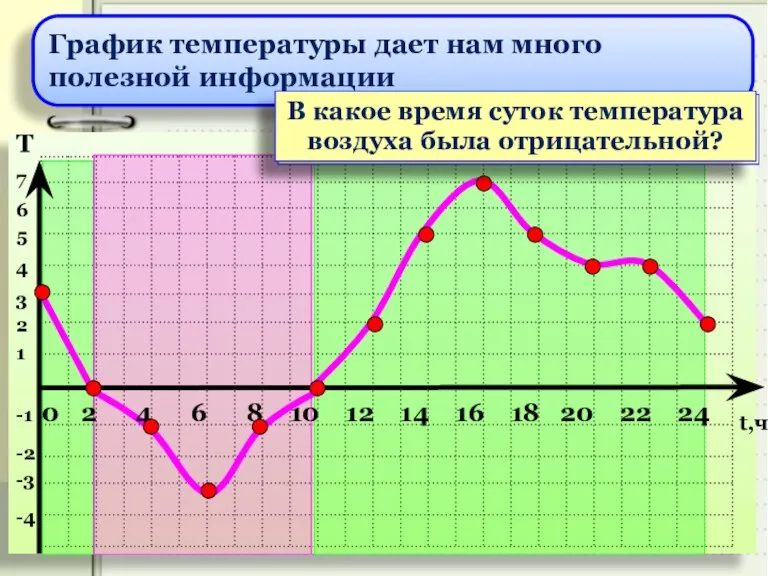
- 7. 0 График температуры дает нам много полезной информации В какое время суток температура воздуха была положительной?
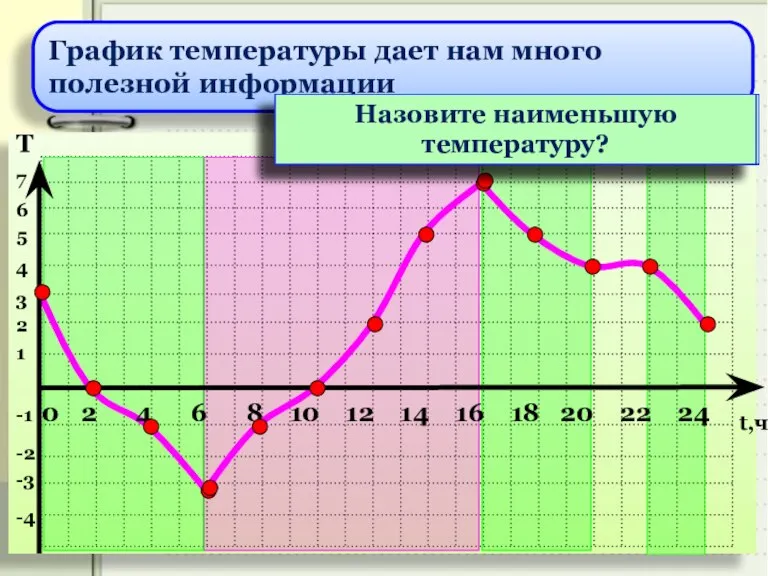
- 8. 0 График температуры дает нам много полезной информации Сколько часов температура воздуха повышалась? В какое время
- 9. Сейсмограф: Используя показания сейсмографов (приборов непрерывно фиксирующих колебания почвы и строящих специальные графики – сейсмограммы) геологи
- 10. Кардиограф: Врачи выявляют болезни сердца, изучая графики, полученные с помощью кардиографа, их называют кардиограммами.
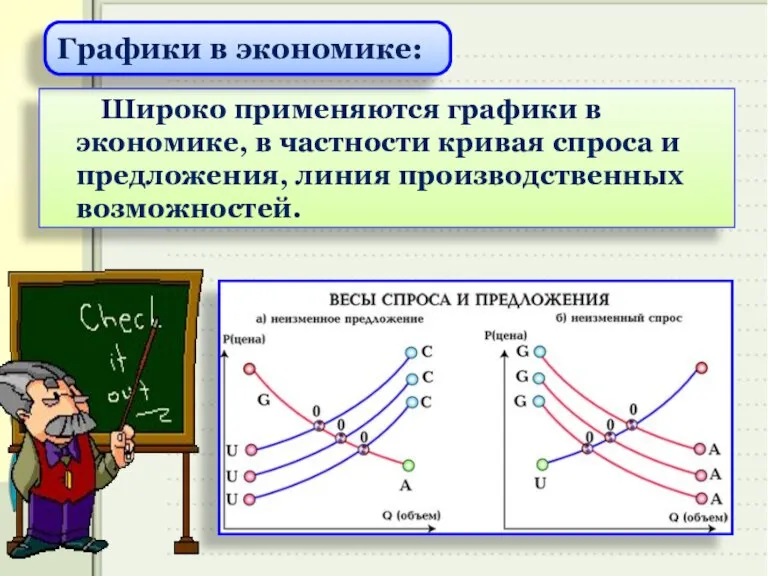
- 11. Широко применяются графики в экономике, в частности кривая спроса и предложения, линия производственных возможностей. Графики в
- 12. Домашнее задание п. 1.6 (знать) № 68, №71 видеоурок: https://youtu.be/cXnhSJH6lkc 29.09.2021
- 13. Тема урока: График функции. 01.10.2021
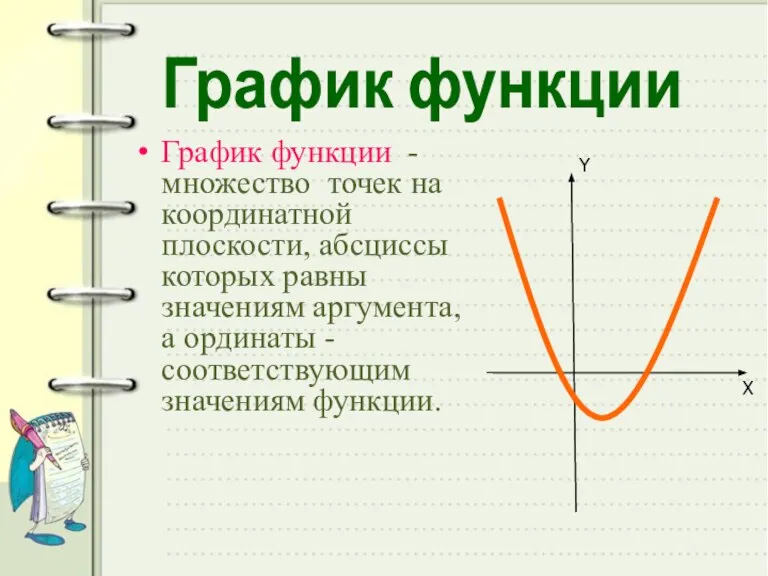
- 14. График функции - множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты -
- 15. Определение функции Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной
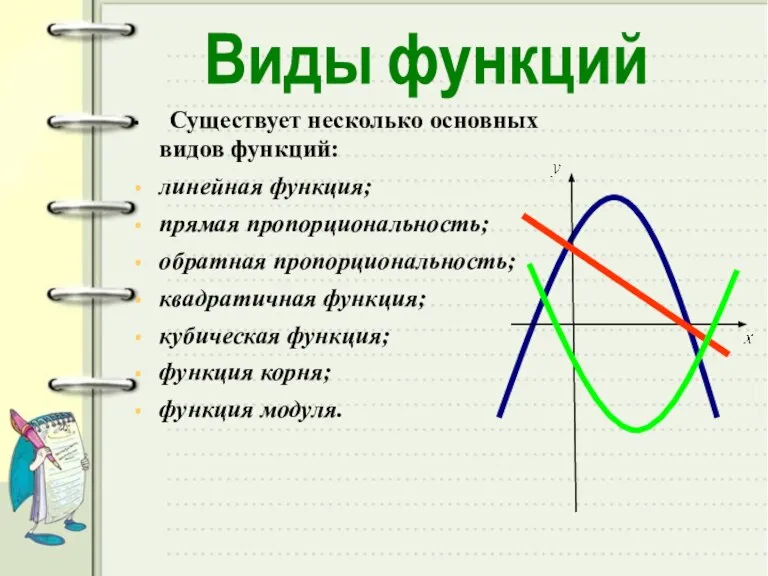
- 16. Существует несколько основных видов функций: линейная функция; прямая пропорциональность; обратная пропорциональность; квадратичная функция; кубическая функция; функция
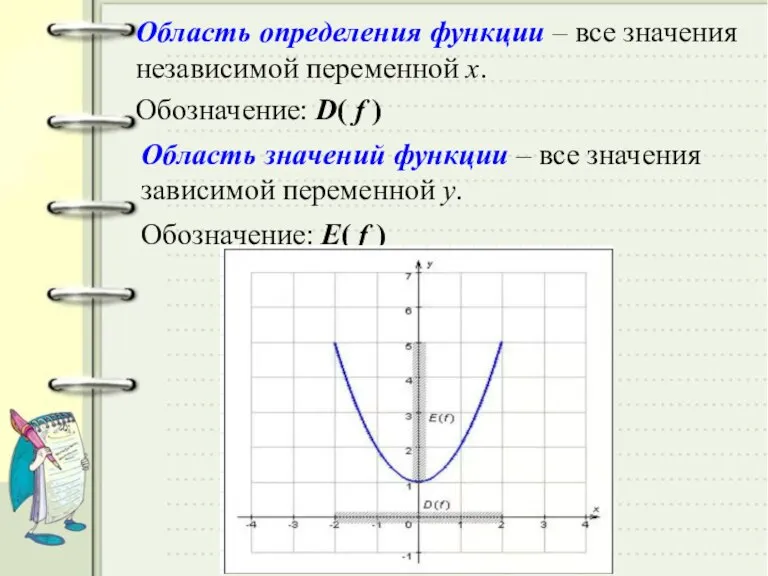
- 17. Область определения функции – все значения независимой переменной х. Обозначение: D( f ) Область значений функции
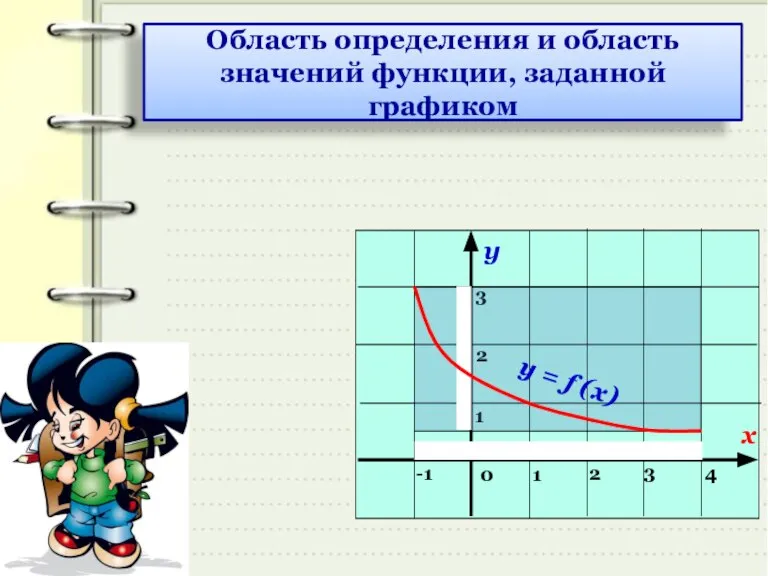
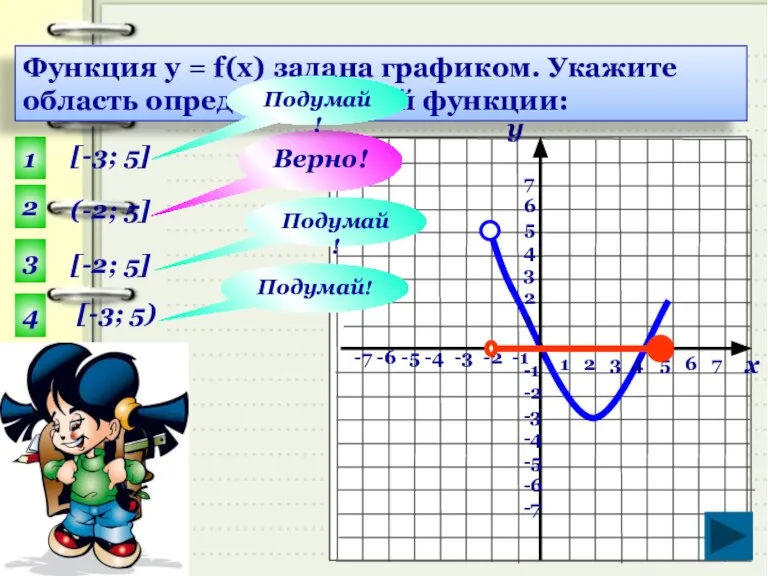
- 18. Область определения и область значений функции, заданной графиком 4 у = f (x)
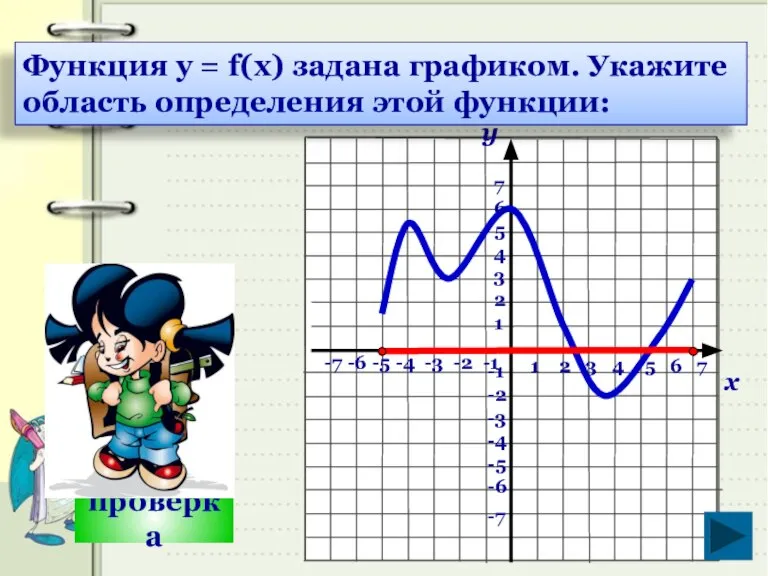
- 19. проверка 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7
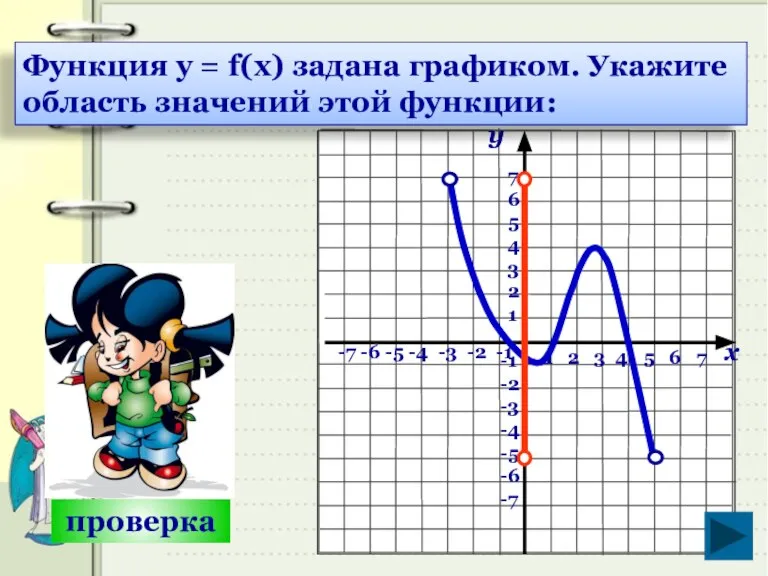
- 20. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6
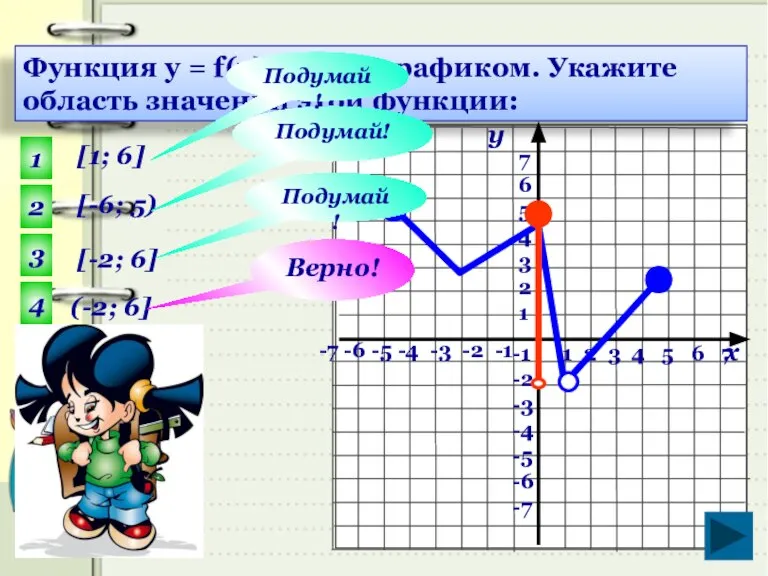
- 21. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6
- 22. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6
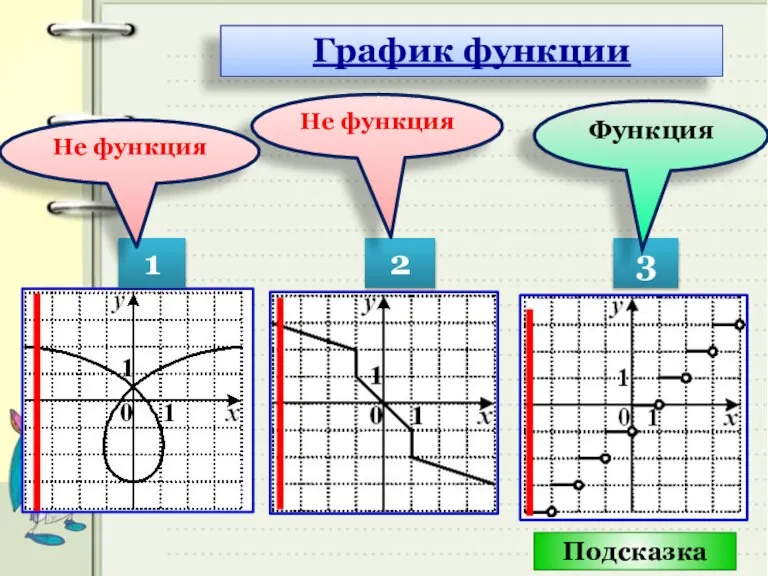
- 23. 1 2 3 Не функция Функция Не функция Подсказка График функции
- 24. Множество точек данной кривой содержит две точки с одной и той же абсциссой х = 2,
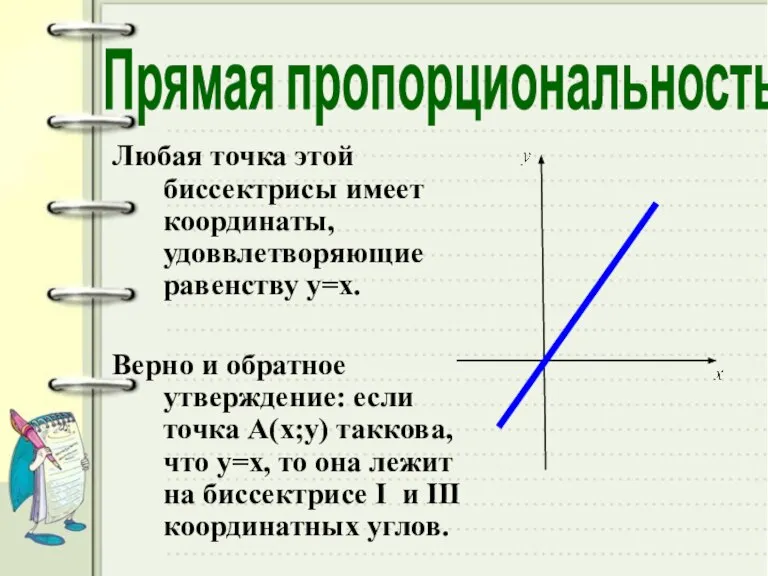
- 25. функция вида y = х D( f ) = R; E( f ) = R; -
- 26. Любая точка этой биссектрисы имеет координаты, удоввлетворяющие равенству у=х. Верно и обратное утверждение: если точка А(х;у)
- 28. Скачать презентацию










 Формулы сложения. Тригонометрические формулы
Формулы сложения. Тригонометрические формулы 3_TEMA_3_Matematicheskaya_logika_1
3_TEMA_3_Matematicheskaya_logika_1 Бинарные отношения
Бинарные отношения Презентация на тему Простые и составные числа
Презентация на тему Простые и составные числа  Поиски математики. Игра
Поиски математики. Игра Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА
Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА  Выборочное наблюдение
Выборочное наблюдение Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Элементы теории вероятностей
Элементы теории вероятностей Функции одной переменной (лекция № 1)
Функции одной переменной (лекция № 1) Линейная регрессия
Линейная регрессия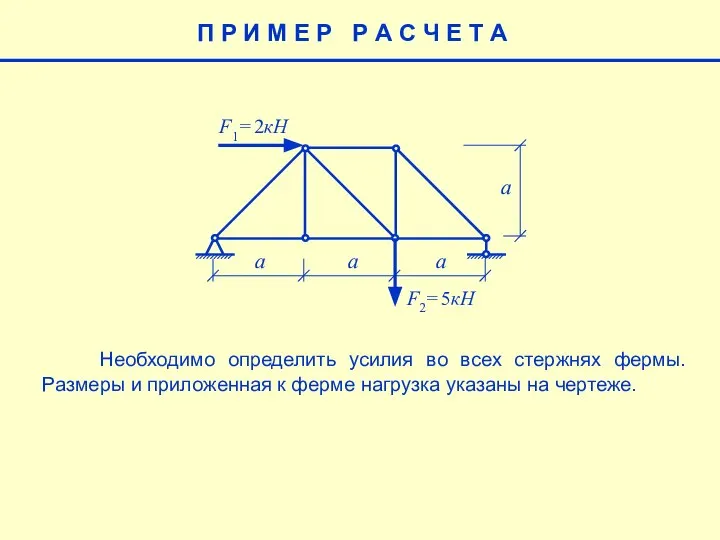 Методы расчета ферм
Методы расчета ферм Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Выборочное наблюдение. Статистическое наблюдение
Выборочное наблюдение. Статистическое наблюдение Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Изучаем геометрические фигуры. Дидактическая игра: На что похоже?
Изучаем геометрические фигуры. Дидактическая игра: На что похоже? 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Презентация на тему КВН по информатике и математике
Презентация на тему КВН по информатике и математике  Презентация на тему Многогранники
Презентация на тему Многогранники  Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Методы оценки рисков проекта
Методы оценки рисков проекта Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Преобразование графиков
Преобразование графиков Множества и операции над ними (9 класс)
Множества и операции над ними (9 класс) Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Геметрические построения. Анимированные алгоритмя
Геметрические построения. Анимированные алгоритмя