Содержание
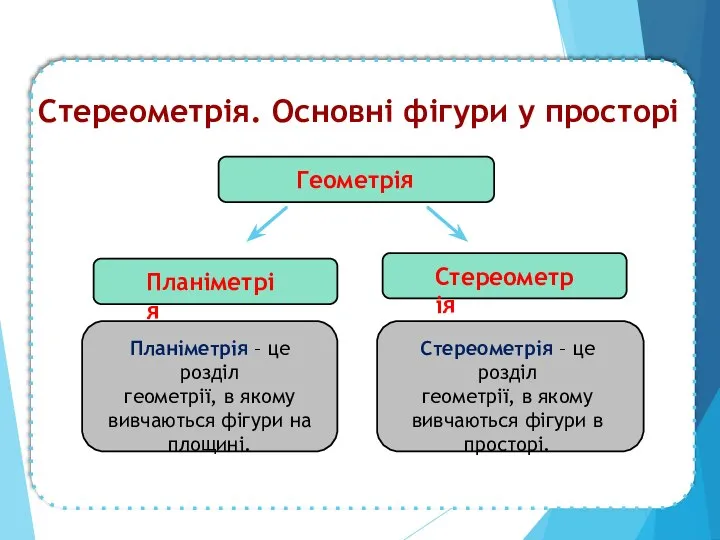
- 2. Стереометрія. Основні фігури у просторі
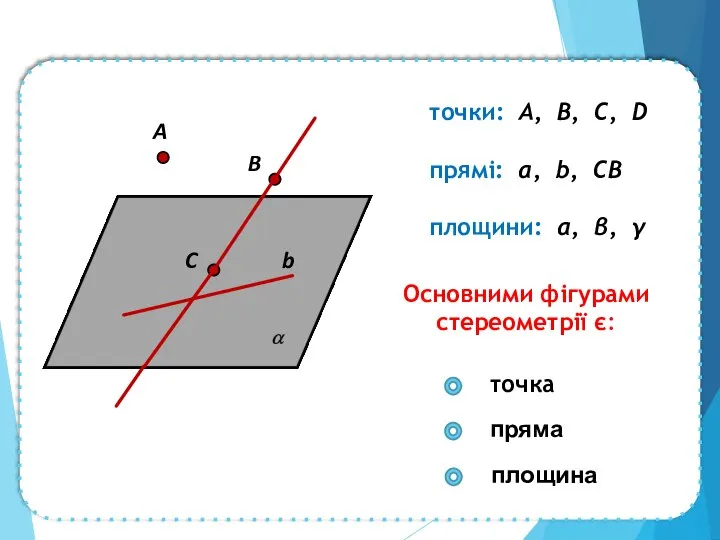
- 3. b Основними фігурами стереометрії є: точки: A, B, C, D прямі: a, b, CB площини: α,
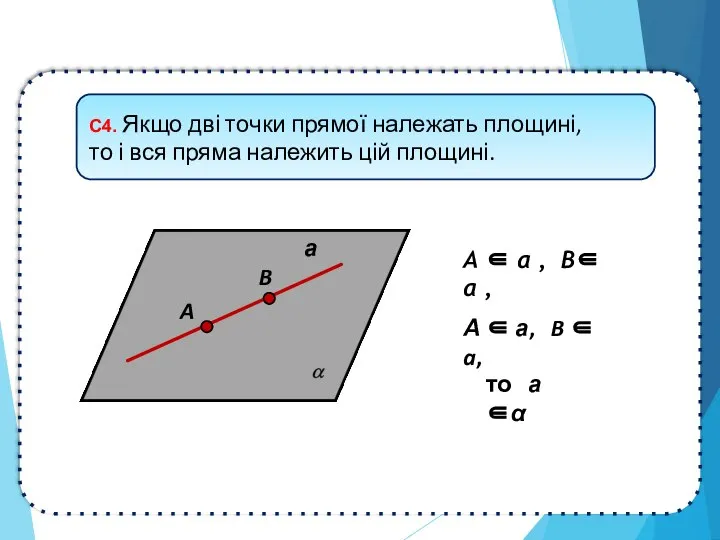
- 4. Точка і пряма – це основні фігури планіметрії, тому в стереометрії справедливі аксіоми планіметрії. Аксіоми стереометрії
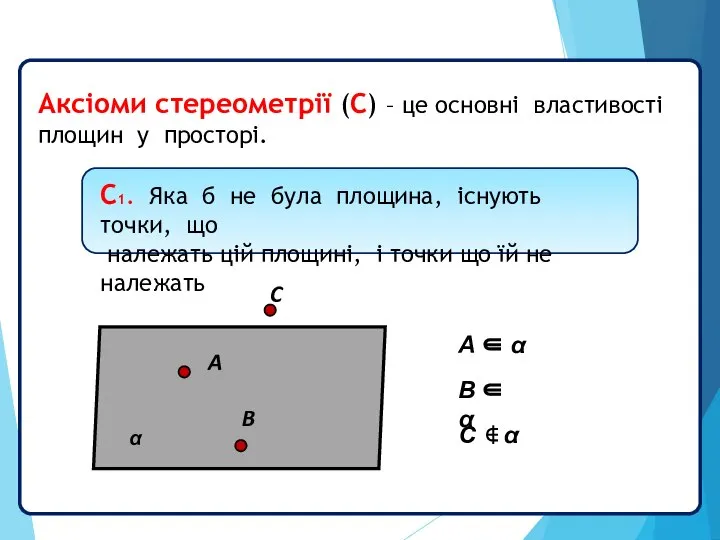
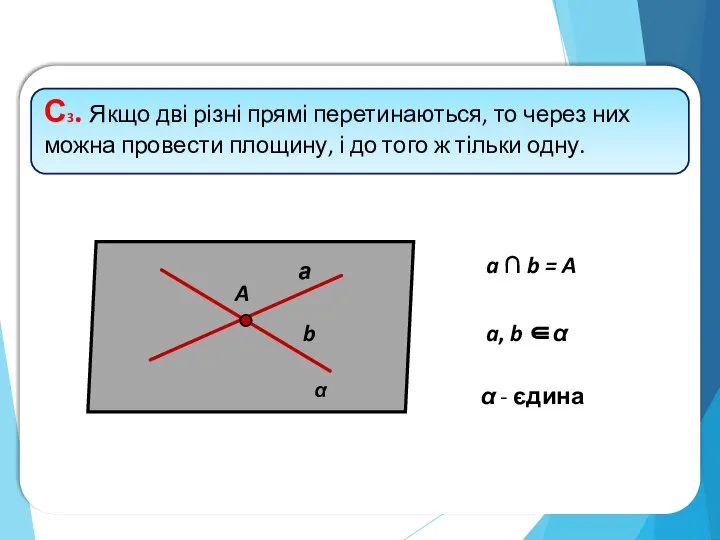
- 5. Аксіоми стереометрії (С) – це основні властивості площин у просторі. α
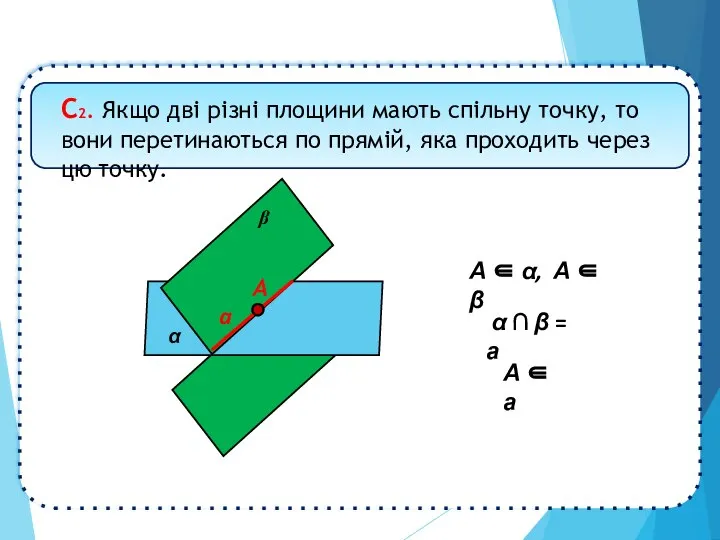
- 6. α β a
- 8. а
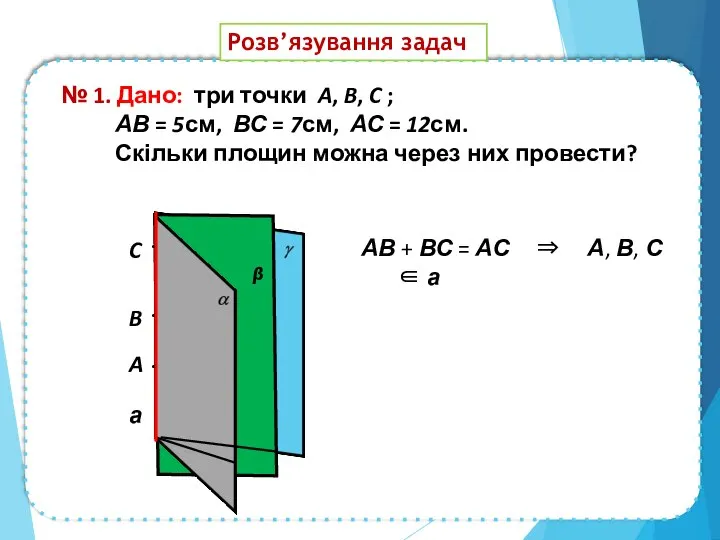
- 9. № 1. Дано: три точки A, B, C ; АВ = 5см, ВС = 7см, АС
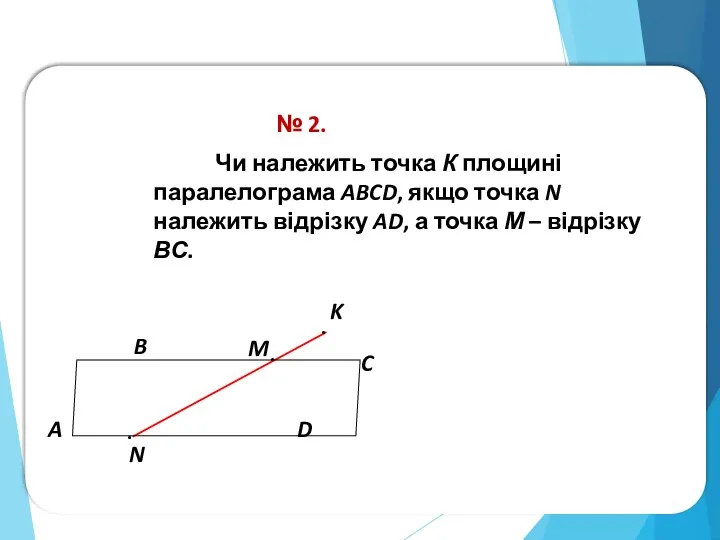
- 10. № 2. Чи належить точка К площині паралелограма ABCD, якщо точка N належить відрізку AD, а
- 12. Скачать презентацию

 Математика
Математика Уравнение с двумя переменными
Уравнение с двумя переменными Повторение изученного. 1 класс
Повторение изученного. 1 класс Прямолинейное неравномерное движение
Прямолинейное неравномерное движение Единица времени - секунда
Единица времени - секунда Проценты и десятичные дроби
Проценты и десятичные дроби Числовыe последовательности
Числовыe последовательности Логарифмы вокруг нас
Логарифмы вокруг нас Решение задач на проценты
Решение задач на проценты Теория вероятностей
Теория вероятностей Тройные и многократные интегралы
Тройные и многократные интегралы Элементы высшей математики
Элементы высшей математики Математика в живописи. (6 класс)
Математика в живописи. (6 класс) Формулы изменившие мир
Формулы изменившие мир Кут. Вимірювання кутів. Рівність кутів. Бісектриса кута
Кут. Вимірювання кутів. Рівність кутів. Бісектриса кута Системы линейных уравнений
Системы линейных уравнений Способ группировки
Способ группировки Логарифмы. Свойства логарифмов
Логарифмы. Свойства логарифмов Перестановка слагаемых
Перестановка слагаемых Преобразование буквенных выражений
Преобразование буквенных выражений Производная. Сумма бесконечной геометрической прогрессии
Производная. Сумма бесконечной геометрической прогрессии Вертикальные углы
Вертикальные углы Алгоритмы нахождения независимого множества
Алгоритмы нахождения независимого множества Матричная алгебра. Лекция 2
Матричная алгебра. Лекция 2 Занятие математического кружка по теме Площадь. 5 класс
Занятие математического кружка по теме Площадь. 5 класс Теорема Пифагора
Теорема Пифагора ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола
ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола Сложение чисел. Тренажер, 1 класс
Сложение чисел. Тренажер, 1 класс