& C) (дистрибутивность конъюнкции относительно дизъюнкции);
16. A ∨ (B & C) ≡ (A ∨ B) & (A ∨ C) (дистрибутивность дизъюнкции относительно конъюнкции);
17. A &(A ∨B) ≡ A (первый закон поглощения);
18. A ∨ (A & B) ≡A (второй закон поглощения);
19. ¬ (A & B) ≡¬ A ∨¬ B (первый закон де Моргана);
20. ¬ (A ∨ B) ≡¬ A &¬ B (второй закон де Моргана);
21. A ≡ (A & B) ∨ (A &¬ B) (первый закон расщепления);
22. A ≡(A ∨ B)&( A ∨¬ B) (второй закон расщепления);
23. A → B ≡¬B→¬ A (закон контрапозиции);
24. A → B ≡¬ A v B = ¬ (A &¬ B);
25. A ~ B ≡ (¬ A ∨B)&(¬ B ∨ A) = (A & B) ∨( ¬ A &¬ B);
26. A ⊕ B = (A &¬ B) ∨ (¬ A & B);
27. A ∨ B = ¬ A → B = ¬ (¬ A &¬ B);
28. A & B = ¬ (A→¬ B) = ¬ (¬ A∨¬ B).
Основные эквивалентные соотношения



















 08.09
08.09 Умножение числа 2 и наа 2
Умножение числа 2 и наа 2 Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Ориентация на плоскости: вверху (верх), внизу (низ), середин. Формируемые понятия
Ориентация на плоскости: вверху (верх), внизу (низ), середин. Формируемые понятия Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Решение задач на разностное и кратное сравнение
Решение задач на разностное и кратное сравнение Обучающие слайды
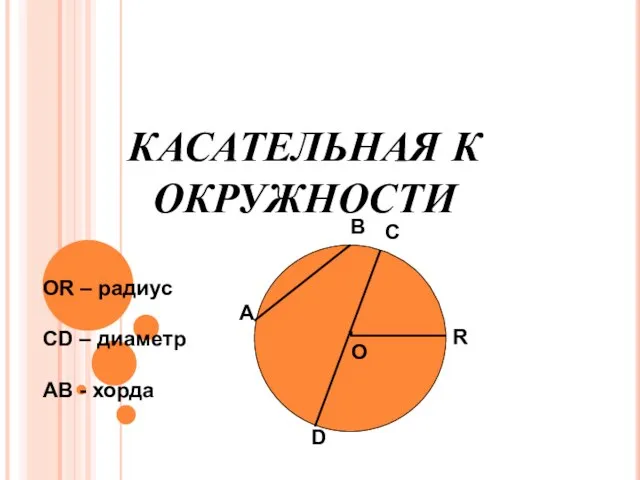
Обучающие слайды Окружность.Круг
Окружность.Круг Свойства степени с натуральным показателем. Задачи
Свойства степени с натуральным показателем. Задачи История числа Пи
История числа Пи Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Тесты по математике
Тесты по математике Межпредметные связи в реализации естественно-математического цикла в средней школе
Межпредметные связи в реализации естественно-математического цикла в средней школе Пирамида. Определение пирамиды. Виды пирамид
Пирамида. Определение пирамиды. Виды пирамид Основы математического моделирования социально-экономических процессов
Основы математического моделирования социально-экономических процессов Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения Сложение смешанных чисел
Сложение смешанных чисел Параллельность в пространстве
Параллельность в пространстве Головоломки. Лабиринты. Магические квадраты
Головоломки. Лабиринты. Магические квадраты Презентация на тему Виды треугольников
Презентация на тему Виды треугольников  Ккомбинаторика. Перестановки. Размещения. Сочетания
Ккомбинаторика. Перестановки. Размещения. Сочетания Числитель и знаменатель
Числитель и знаменатель Перенос запятой в положительной десятичной дроби
Перенос запятой в положительной десятичной дроби Действия с дробями
Действия с дробями Признаки параллелограмма
Признаки параллелограмма Презентация на тему Измерение высоты предмета
Презентация на тему Измерение высоты предмета  Проценты в нашей жизни
Проценты в нашей жизни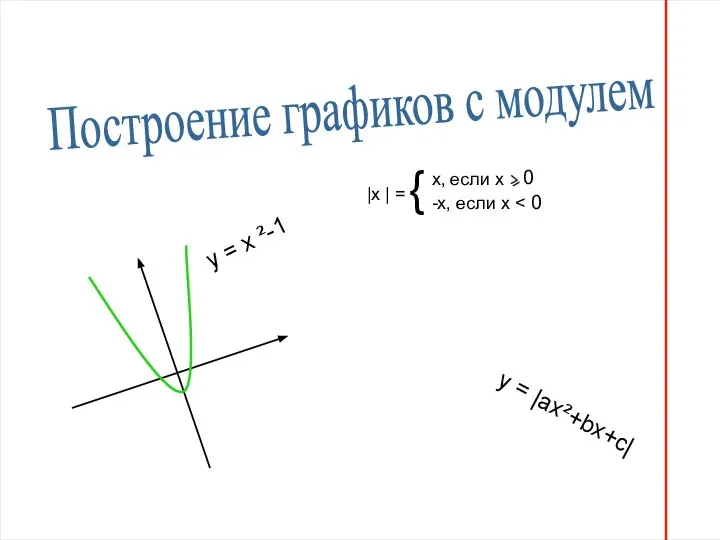 Построение графиков с модулем
Построение графиков с модулем