Содержание
- 2. Мотивирующая задача. Существует ли параллелограмм с углом 27° между диагоналями ?
- 3. Проблема: Появились задачи, которые невозможно решить известными методами. Цель : отыскать новый метод решения и использовать
- 4. Гипотеза: Если какая – либо величина меняется непрерывно в течение некоторого времени и в начальный момент
- 5. Практическое подтверждение гипотезы. 1 Изготовлена модель, диагоналей параллелограмма, состоящая из двух реек, подвижно закрепленных в их
- 6. Практическое подтверждение гипотезы 2 Пусть минутная стрелка часов сейчас на отметке 5, тогда спустя 10 минут
- 7. Практическое подтверждение гипотезы 3 При изучении функций мы изображали их графики. Очевидно , что ряд процессов
- 8. Например. График зависимости величины y от времени Выглядит так: Тогда очевидно что величина y в промежуток
- 9. Получить доказательство этого факта мне не удалось по ряду причин. Главная из которых отсутствие знания математического
- 10. Задача2 Дан квадрат, его диагональ 2 см. В нем проводят отрезки, параллельные диагоналям, с концами на
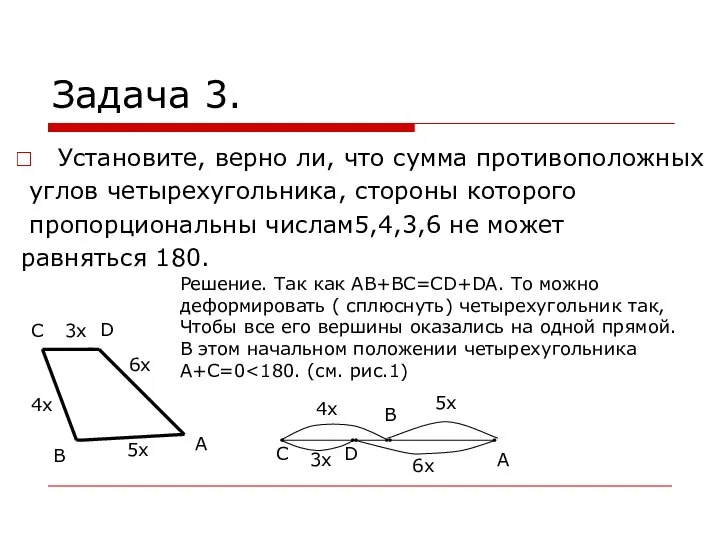
- 11. Задача 3. Установите, верно ли, что сумма противоположных углов четырехугольника, стороны которого пропорциональны числам5,4,3,6 не может
- 12. Будем теперь сжимать четырехугольник в направлении AC до тех пор, пока вершина С не окажется на
- 13. Задача 4. В параллелограмме одна сторона 10см, а другая 8см. Найдите длину диагонали, если это возможно
- 15. Скачать презентацию











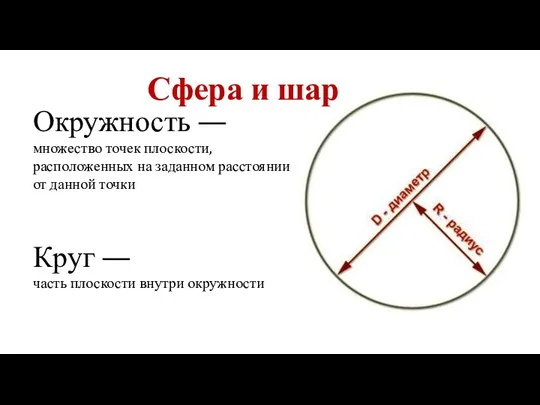 Сфера и шар
Сфера и шар Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Деление. Неправильные дроби
Деление. Неправильные дроби Геометрия в живописи
Геометрия в живописи Угол между прямой и плоскостью
Угол между прямой и плоскостью Задачи на прогрессию
Задачи на прогрессию Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Степенная функция
Степенная функция Уравнение Бернулли
Уравнение Бернулли Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Площадь поверхности цилиндра
Площадь поверхности цилиндра Параллельные прямые
Параллельные прямые Ромб. Решение 6 задачи
Ромб. Решение 6 задачи Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики B7
B7 Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2)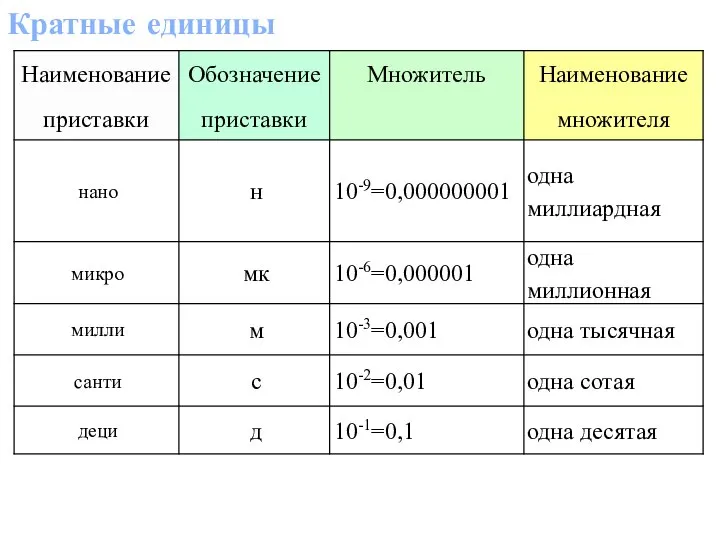 Кратные единицы
Кратные единицы Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2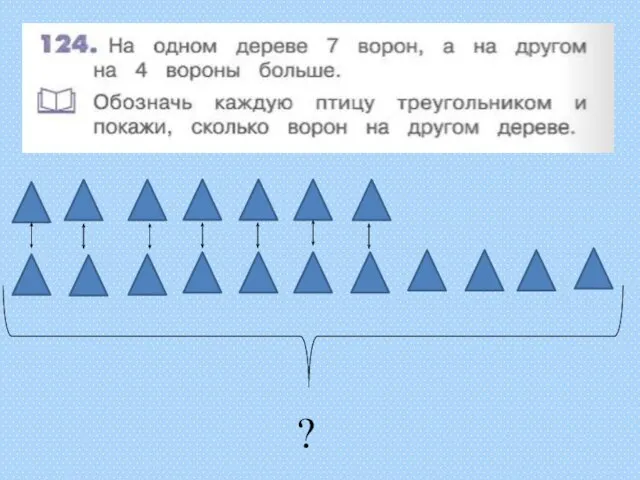 Треугольники, задача
Треугольники, задача Прямоугольник
Прямоугольник Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Олимпиадная математика. Доказательство от противного
Олимпиадная математика. Доказательство от противного Естественно балансирующееся общество
Естественно балансирующееся общество ریاضی جزوه کامل
ریاضی جزوه کامل Таблица Шульте
Таблица Шульте Понятие производной
Понятие производной Почти все об углах
Почти все об углах