Содержание
- 2. Секции Определения, термины и примеры применения Sergey Mityagin Виды регрессионного анализа Коэффициенты регрессии и детерминации Линейная
- 3. Примеры применения Sergey Mityagin 1. Моделирование числа поступивших в университет для лучшего понимания факторов, удерживающих детей
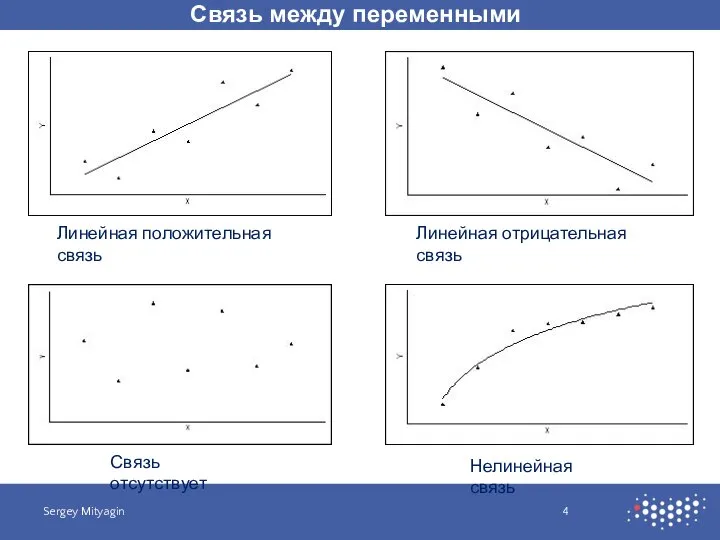
- 4. Связь между переменными Sergey Mityagin Линейная положительная связь Линейная отрицательная связь Связь отсутствует Нелинейная связь
- 5. Определения Sergey Mityagin Регрессионный анализ — статистический метод исследования влияния одной или нескольких независимых переменных X
- 6. Определения Sergey Mityagin Цели регрессионного анализа 1. Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми
- 7. Термины Sergey Mityagin Уравнение регрессии Математическая формула, применяемая к независимым переменным, чтобы лучше спрогнозировать зависимую переменную,
- 8. Термины Sergey Mityagin Формирование уравнения регрессии – процедура минимизации случайного остатка. Выделение зависимых переменных Выделение смещения
- 9. Определения Sergey Mityagin
- 10. Секции Определения, термины и примеры применения Sergey Mityagin Виды регрессионного анализа Коэффициенты регрессии и детерминации Линейная
- 11. Виды регрессионного анализа Sergey Mityagin Линейные по переменным Не линейные по переменным Линейные по параметрам Не
- 12. Линейный регрессионный анализ Sergey Mityagin Запись в матричной форме:
- 13. Линейный регрессионный анализ Sergey Mityagin Оценка параметров: Получаем в явном виде набор уравнений: МНК:
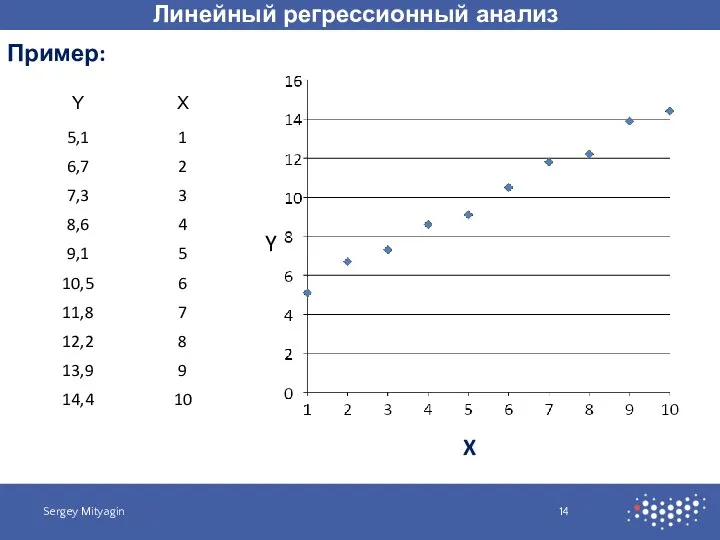
- 14. Линейный регрессионный анализ Sergey Mityagin Пример: X Y
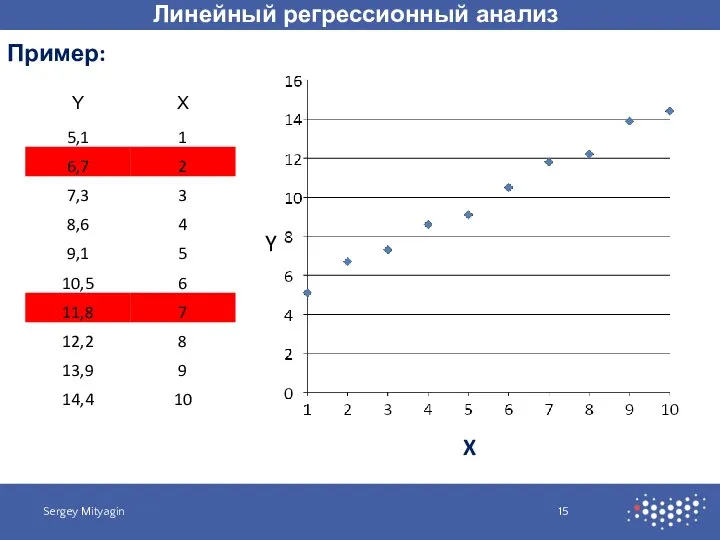
- 15. Линейный регрессионный анализ Sergey Mityagin Пример: X Y
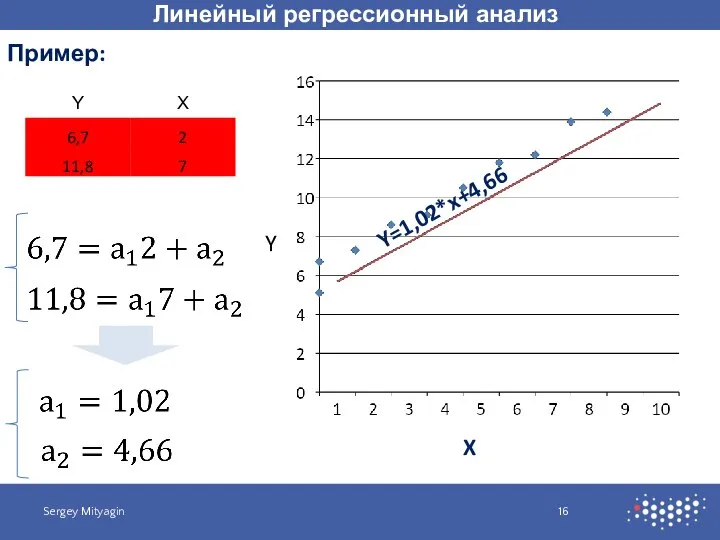
- 16. Линейный регрессионный анализ Sergey Mityagin Пример: X Y Y=1,02*x+4,66
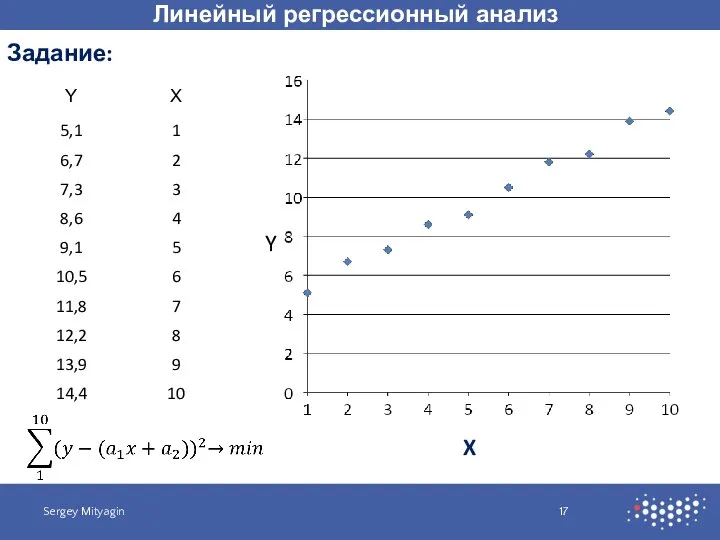
- 17. Линейный регрессионный анализ Sergey Mityagin Задание: X Y
- 18. Другие виды регрессионного анализа Sergey Mityagin Полиномиальная функция регрессии: Запись в матричной форме:
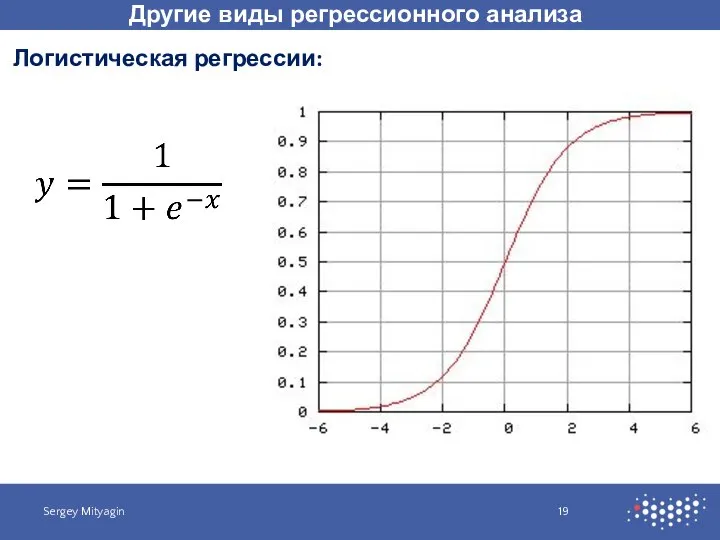
- 19. Другие виды регрессионного анализа Sergey Mityagin Логистическая регрессии:
- 20. Секции Определения, термины и примеры применения Sergey Mityagin Виды регрессионного анализа Коэффициенты регрессии и детерминации Линейная
- 21. Смысл коэффициента регрессии Sergey Mityagin Свойства коэффициента регрессии • Коэффициент регрессии может принимать любые значения. •
- 22. Коэффициент детерминации Sergey Mityagin Коэффициент детерминации рассматривают, как правило, в качестве основного показателя, отражающего меру качества
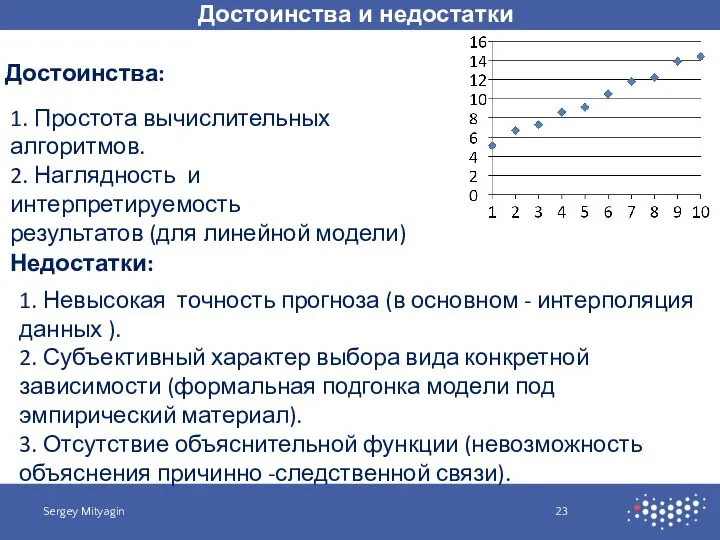
- 23. Достоинства и недостатки Sergey Mityagin Достоинства: Недостатки: 1. Простота вычислительных алгоритмов. 2. Наглядность и интерпретируемость результатов
- 24. Секции Определения, термины и примеры применения Sergey Mityagin Виды регрессионного анализа Коэффициенты регрессии и детерминации Линейная
- 25. Линейная регрессия на корреляции Sergey Mityagin Линейная регрессия на корреляции — частный случай линейной регрессии. Применяется
- 27. Скачать презентацию

















 Презентация на тему Число и цифра 9
Презентация на тему Число и цифра 9  Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) Структура арифметической задачи
Структура арифметической задачи Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Геометрия. Решение задач
Геометрия. Решение задач Страна геометрических фигур
Страна геометрических фигур Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Відстань між двома точками. Координати середини відрізка
Відстань між двома точками. Координати середини відрізка Прямая и плоскость
Прямая и плоскость Неравенства с двумя переменными
Неравенства с двумя переменными Функция y = x2 и её график
Функция y = x2 и её график Существование треугольника, равного данному (7 класс)
Существование треугольника, равного данному (7 класс) Смешанные дроби. 5 клас
Смешанные дроби. 5 клас Математика как наука. Матем методы
Математика как наука. Матем методы Признаки делимости
Признаки делимости Графы. Пути с таблицами
Графы. Пути с таблицами Практикум по эконометрике
Практикум по эконометрике Решение задач
Решение задач Построение сечений тетраэдра
Построение сечений тетраэдра Углы в пространстве. Перпендикулярность плоскостей
Углы в пространстве. Перпендикулярность плоскостей Страна Математика
Страна Математика Степени числа
Степени числа Поворот
Поворот Форма вариаций
Форма вариаций Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Числительные. Количественные числительные
Числительные. Количественные числительные Преобразование графиков
Преобразование графиков Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)