Содержание
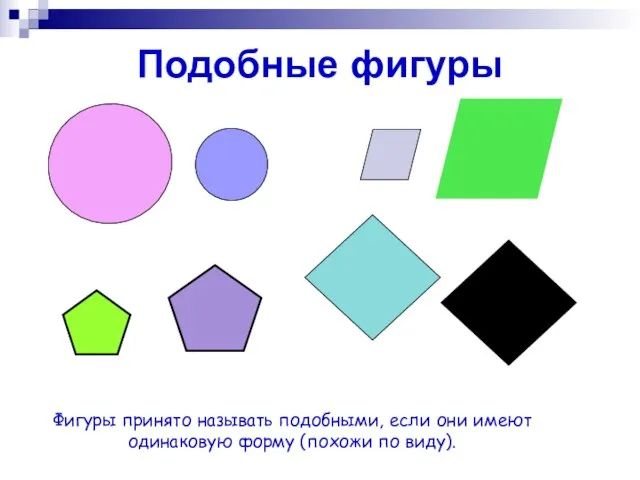
- 3. Подобные фигуры Фигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
- 4. Подобие в жизни
- 5. Подобие в жизни
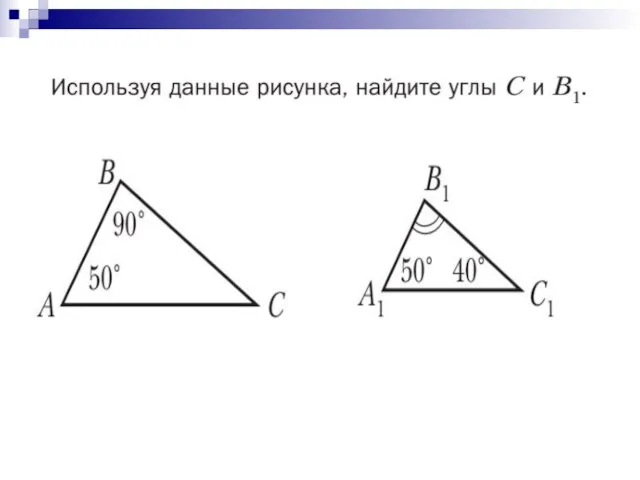
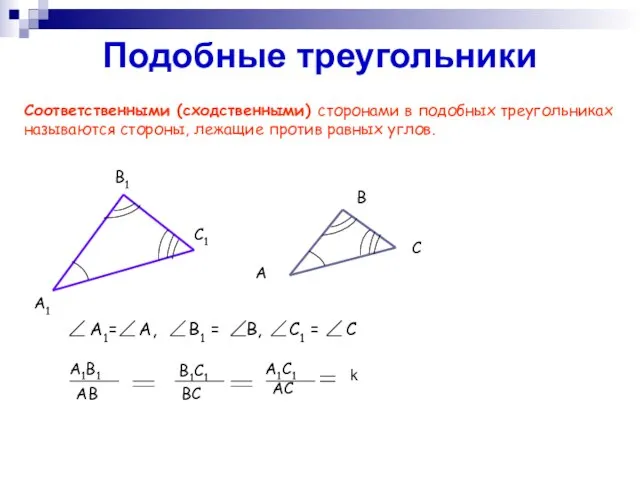
- 6. Подобные треугольники Соответственными (сходственными) сторонами в подобных треугольниках называются стороны, лежащие против равных углов.
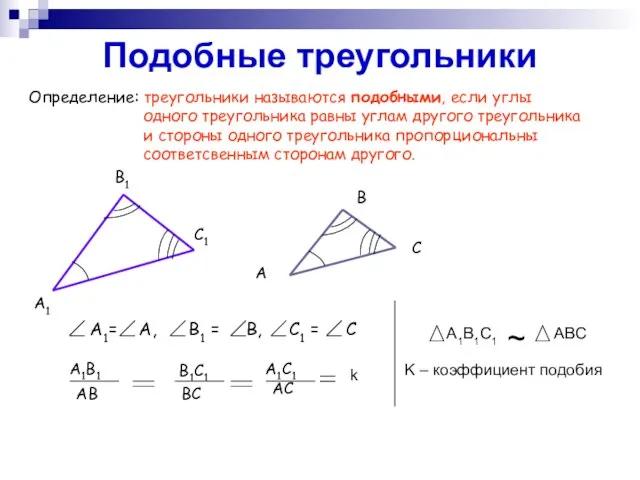
- 7. Подобные треугольники Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны
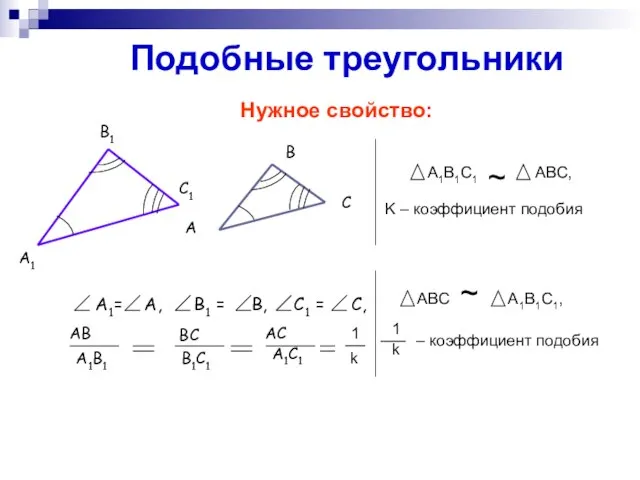
- 8. Подобные треугольники Нужное свойство:
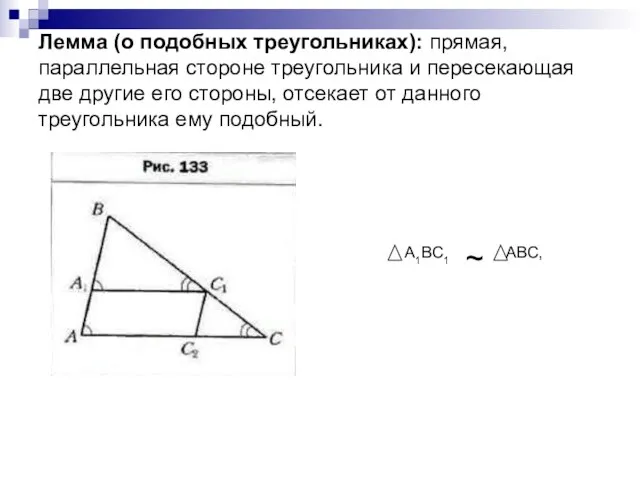
- 9. Лемма (о подобных треугольниках): прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от
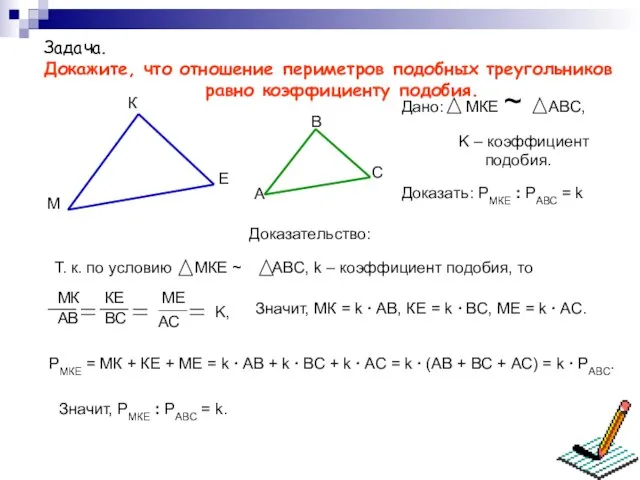
- 10. Задача. Докажите, что отношение периметров подобных треугольников равно коэффициенту подобия. Доказательство: Значит, МК = k ∙
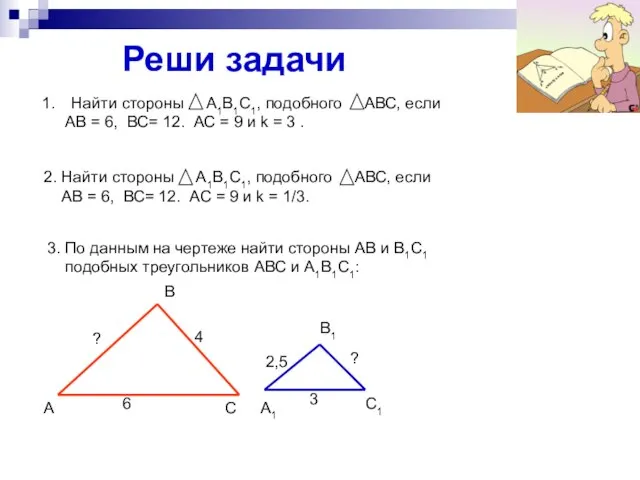
- 11. Реши задачи № 423-426, 430, 432
- 12. Реши задачи
- 14. Скачать презентацию



 32046
32046 Признак параллельности прямых. Задачи для устной работы
Признак параллельности прямых. Задачи для устной работы Показатели вариации
Показатели вариации Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Геометрические тела. Многогранники
Геометрические тела. Многогранники Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Понятие производной
Понятие производной Tema1_TeoriaMnozhestv
Tema1_TeoriaMnozhestv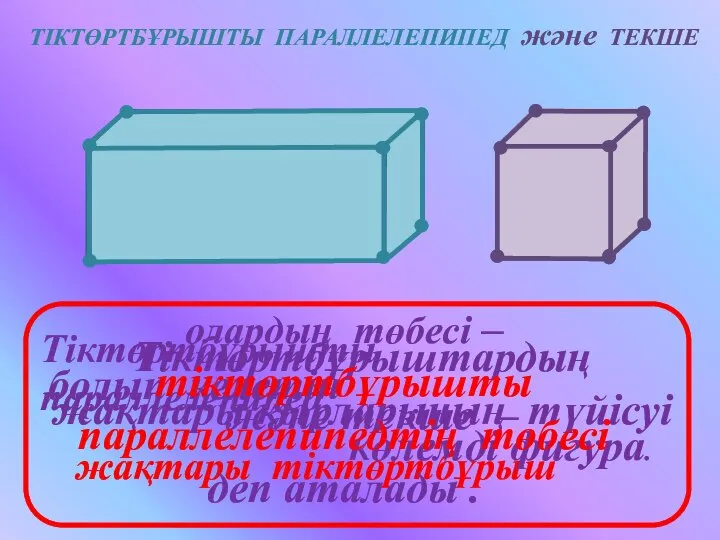 Тіктөртбұрышты параллелепипед және текше
Тіктөртбұрышты параллелепипед және текше Свойства логарифмов
Свойства логарифмов Элементы геометрии на небесной сфере. Лекция 1
Элементы геометрии на небесной сфере. Лекция 1 Признаки параллелограмма
Признаки параллелограмма Найдите все значения параметра a,
Найдите все значения параметра a, аксиомы стереометрии
аксиомы стереометрии Практикум по решению задач практической направленности
Практикум по решению задач практической направленности Умножение дробей
Умножение дробей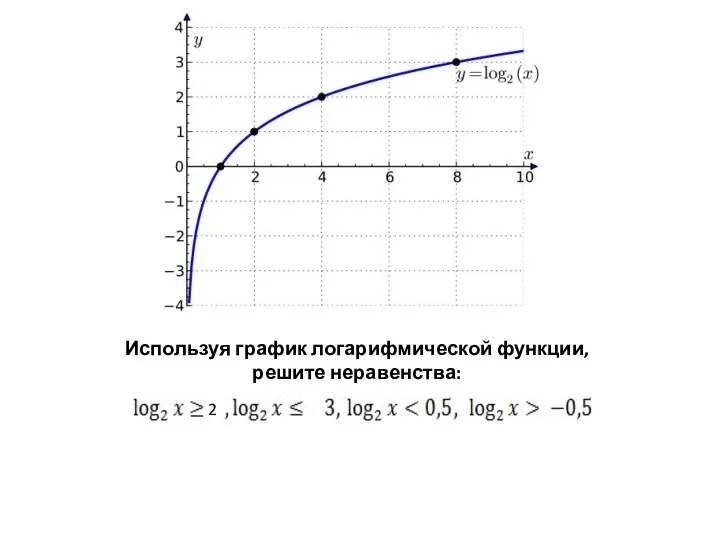 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма
Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма угол между прямой и плоскостью (1)
угол между прямой и плоскостью (1) Учимся писать цифры
Учимся писать цифры Векторы. Нулевой вектор
Векторы. Нулевой вектор Сравнение дробей. 1 часть
Сравнение дробей. 1 часть Живая планета!
Живая планета! Преобразование иррациональных выражений
Преобразование иррациональных выражений Арифметичская прогрессия
Арифметичская прогрессия Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника